Файл: Расчет сечения смещения атома электроном в свинце на основе метода лиджиана кинга женгминга и его модификаций.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
РАСЧЕТ СЕЧЕНИЯ СМЕЩЕНИЯ АТОМА ЭЛЕКТРОНОМ В СВИНЦЕ НА ОСНОВЕ МЕТОДА ЛИДЖИАНА – КИНГА – ЖЕНГМИНГА И ЕГО МОДИФИКАЦИЙ
Кац Петр Борисович,
к.ф-м.н., доцент
Римашевская Анастасия Сергеевна,
Магистрант
БрГУ имени А.С. Пушкина
Аннотация: Вычислены коэффициенты dZ для трижды модифицированного метода LQZ для свинца. Рассчитано сечение первичного смещения атома и полное сечение смещения атома в свинце для ряда энергий с помощью трижды модифицированного метода LQZ. Также заново рассчитаны сечения смещения атома в уране, плутонии и эйнштейнии с корректировкой пороговой энергии смещения. Корректировка приводит к уменьшению погрешности. Модифицированные методы приводят в среднем к меньшей погрешности, чем обычный метод LQZ.
Ключевые слова: сечение смещения атома, метод Лиджиана – Кинга – Женгминга, модифицированные варианты метода LQZ.
CALCULATION OF THE DISPLACEMENT CROSS SECTION
BY AN ELECTRON IN LEAD BASED ON THE LIGIAN – QING – ZHENGMING METHOD AND ITS MODIFICATIONS
Kats Piotr Borisovich
Rymasheuskaya Anastasiya Sergeevna
Abstract: The coefficients dZ for the thrice modified LQZ method for lead are calculated. The primary displacement cross section and the total displacement cross section in lead for a number of energies are calculated using the thrice modified LQZ method. Also, the atomic displacement cross sections in uranium, plutonium and einsteinium were calculated anew with the correction of the threshold displacement energy. The correction leads to a decrease in the error. The modified methods lead to a lower error on average than the usual LQZ method.
Key words: displacement cross section, Ligian – Qing – Zhengming method, modified versions of the LQZ method.
Известно [1], что облучение различных материалов быстрыми частицами приводят к выбиванию атомов из узлов кристаллической решетки, что приводит к изменению структуры и свойств материалов. Такое воздействие имеет место в ядерных и термоядерных реакторах, ускорителях, космических аппаратах. Если энергия, переданная атому, превышает пороговую энергию смещения для данного вещества, то атом смещается. Такой атом называют первично выбитым атомом ПВА. Если энергия ПВА достаточно велика, то он может выбить другие атомы. Вероятность смещения атома характеризуется сечением смещения атома. В зависимости от того, учитывается ли только смещение ПВА или также вторичные смещения, различают сечение первичного смещения σ
p и полное сечение смещения σtot [2].
Вследствие малой массы электронов выбивать атомы из узлов кристаллической решетки могут только релятивистские электроны, поэтому для расчета сечения смещения атома требуется нахождение интеграла от моттовского дифференциального сечения рассеяния релятивистских электронов [3]. Так как это сечение выражается через условно сходящиеся ряды по полиномам Лежандра, то такое интегрирование является весьма сложной задачей. Иногда для упрощения расчетов используют второе борновское приближение [4], но погрешность этого приближения очень велика для тяжелых атомов. Очень хорошую точность дает применение метода Лиджиана – Кинга – Женгминга LQZ [5].
В [6–8] вычислялось сечение первичного смещения атомов в свинце, уране, плутонии и эйнштейнии и полное сечение смещения атомов в уране, плутонии и эйнштейнии на основе метода LQZ и его второй и третьей модификаций [9; 10]. Результаты расчетов сравнивались с приведенными в [2]. Всегда отмечалась сравнительно высокая погрешность при энергии электронов вблизи пороговой энергии.
Как отмечено в [8], минимальная энергия электрона Ed, вызывающая смещение атома Ed, вычисленная из условия равенства максимальной переданной при столкновении с атомом энергии пороговой энергии не совпадает точно с указываемой в [2] для данной относительной атомной массы и пороговой кинетической энергии атома Тd. Если подобрать Тd так, чтобы Ed совпало c приведенным в [2], результаты расчетов с помощью аналитических приближений оказываются ближе к результатам численных расчетов [2].
В представленной работе мы скорректировали Тd для свинца, урана, плутония и эйнштейния и пересчитали значения сечения смещения. Также мы рассчитали сечения первичного смещения методом LQZm3 [10] для свинца и полные сечения смещения для свинца методами LQZ, LQZm2 и LQZm3. Соответствующие формулы для расчета сечений можно посмотреть в [7–9].
В таблице 1 приводятся значения коэффициентов dZ для метода LQZm3 для свинца.
Таблица 1
Коэффициенты для трижды модифицированного метода LQZ для свинца
| j/k | 1 | 2 | 3 | 4 | 5 |
| 1 | 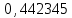 | 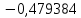 | 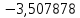 | 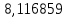 | 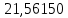 |
| 2 | 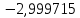 | 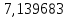 | 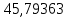 | 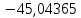 | 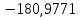 |
| 3 | 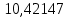 | 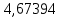 | 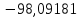 | 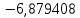 | 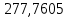 |
| 4 | 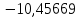 | 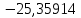 | 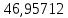 | 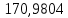 | 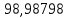 |
| 5 | 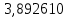 |  | 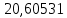 | 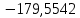 | 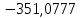 |
| 6 | 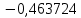 | 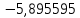 | 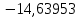 | 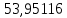 | 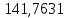 |
В таблице 2 приводится значение усредненной по скоростям ошибки
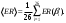
Выражение для ER см. в [5]. Средняя относительная ошибка для трижды модифицированного метода больше, чем для дважды модифицированного, но меньше, чем для обычного.
Таблица 2
Cреднее арифметическое значение относительной ошибки, %
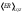 | 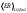 | 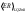 |
| 0,97 | 0,43 | 0,58 |
В таблице 3 приведены значения сечения первичного смещения атома в зависимости от энергии. Для значения пороговой энергии электрона 0,680176 МэВ [2] необходимо принять Td = 11,99678 эВ. В скобках для первых пяти значений приведены относительные погрешности в процентах. Они заметно снизились после корректировки пороговой энергии смещения атома.
Таблица 3
Свинец. Сечение первичного смещения атома
| Z = 82, М = 207,21, Td = 11,99678 эВ | |||||||
| E, МэВ | 0,686 | 0,693 | 0,707 | 0,727 | 0,754 | 0,789 | 0,829 |
| σpLQZ | 3,01 (1,1) | 6,88 (1,0) | 15,38 (0,62) | 29,01 (0,24) | 49,46 (0,09) | 78,26 | 112,71 |
| σpLQZmod2 | 3,035 (0,16) | 6,928 (0,32) | 15,43 (0,33) | 28,97 (0,38) | 49,23 (0,38) | 77,73 | 111,90 |
| σpLQZmod3 | 3,046 | 6,97 | 15,58 | 29,32 | 49,84 | 78,52 | 112,65 |
| σpO | 3,04 | 6,95 | 15,48 | 29,08 | 49,42 | 77,98 | 112,13 |
| E, МэВ | 0,884 | 0,952 | 1,05 | 1,19 | 1,36 | 1,56 | 1,83 |
| σpLQZ | 160,41 | 217,02 | 290,44 | 376,18 | 452,87 | 513,62 | 561,76 |
| σpLQZmod2 | 159,35 | 215,93 | 289,67 | 376,11 | 453,51 | 514,59 | 562,57 |
| σpLQZmod3 | 159,48 | 215,42 | 287,94 | 373,38 | 450,74 | 512,65 | 561,87 |
| σpO | 159,68 | 215,75 | 289,11 | 375,21 | 452,69 | 514,18 | 562,78 |
| E, МэВ | 2,17 | 2,58 | 3,06 | 3,53 | 4,08 | 4,76 | 5,78 |
| σpLQZ (δ) | 589,65 | 598,20 | 592,48 | 580,39 | 563,95 | 544,03 | 518,06 |
| σpLQZmod2 | 589,91 | 597,89 | 591,81 | 579,66 | 563,36 | 543,77 | 518,36 |
| σpLQZmod3 | 590,09 | 598,17 | 591,66 | 579,00 | 562,27 | 542,44 | 517,12 |
| σpO | 590,56 | 598,58 | 592,18 | 579,66 | 562,94 | 543,00 | 517,52 |
| E, МэВ | 6,8 | 10,2 | 13,6 | 20,4 | 34 | 68 | 136 |
| σpLQZ | 497,18 | 453,29 | 430,50 | 408,71 | 393,40 | 384,39 | 381,08 |
| σpLQZmod2 | 497,99 | 455,14 | 432,74 | 411,00 | 395,21 | 385,26 | 381,26 |
| σpLQZmod3 | 497,10 | 455,69 | 434,26 | 413,35 | 397,74 | 387,22 | 382,51 |
| σpO | 497,32 | 455,75 | 435,29 | 414,38 | 397,13 | 386,67 | 378,67 |
В таблице 4 приводятся результаты для полного сечения смещения. σO – сечение смещения по результатам численных расчетов [2]. Также, как в [2] для расчета полного сечения смещения использовалась каскадная модель Кинчина – Пиза. Так как до энергии 1,19 МэВ согласно модели Кинчина – Пиза ПВА не могут вызывать смещений атомов, то полное сечение смещения совпадает с сечением первичного смещения.
Таблица 4
Свинец. Полное сечение смещения атома
| E, МэВ | 1,19 | 1,36 | 1,56 | 1,83 | 2,17 | 2,58 |
| σtotLQZ | 376,97 | 460,81 | 539,65 | 623,98 | 707,20 | 786,18 |
| σtotLQZmod2 | 376,91 | 461,39 | 540,45 | 624,58 | 707,30 | 785,80 |
| σtotLQZmod3 | 374,18 | 458,68 | 538,55 | 623,80 | 707,30 | 785,99 |
| σtotO | 376,03 | 460,58 | 540,07 | 624,80 | 707,94 | 786,53 |
| E, МэВ | 3,06 | 3,53 | 4,08 | 4,76 | 5,78 | 6,8 |
| σtotLQZ (δ) | 859,91 | 919,25 | 977,66 | 1038,41 | 1113,39 | 1175,27 |
| σtotLQZmod2 | 859,24 | 918,51 | 977,01 | 1037,99 | 1113,41 | 1175,73 |
| σtotLQZmod3 | 859,20 | 918,13 | 976,31 | 1037,05 | 1112,41 | 1174,86 |
| σtotO | 859,77 | 918,76 | 976,92 | 1037,60 | 1112,86 | 1175,19 |
| E, МэВ | 10,2 | 13,6 | 20,4 | 34 | 68 | 136 |
| σtotLQZ | 1327,75 | 1435,29 | 1586,87 | 1778,39 | 2039,38 | 2301,28 |
| σtotLQZmod2 | 1329,40 | 1437,71 | 1590,15 | 1782,33 | 2043,61 | 2305,32 |
| σtotLQZmod3 | 1329,42 | 1438,61 | 1592,27 | 1785,74 | 2048,16 | 2310,51 |
| σtotO | 1329,45 | 1439,26 | 1592,75 | 1785,33 | 2047,87 | 2306,42 |