Файл: 1. Форма и размеры Земли (физ поверхность, геоид, эллипсоид).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 409
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Форма и размеры Земли (физ. поверхность, геоид, эллипсоид)
Знание фигуры и размеров Земли необходимо прежде всего для правильного изображения земной поверхности в виде карт и планов
1.Физическая поверхность – совокупность всех неровностей суши и дна океанов, а также поверхности воды. Она не может быть выражена конечным математическим уравнением, поэтому используется для решения лишь некоторых практических задач геодезии.
Геоид - тело принятое за теоретическую фигуру Земли, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками, Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически, что необходимо для решения геодезических задач.
3.Поверхность эллипсоида получается при вращении эллипса вокруг малой (полярной) полуоси. Эллипсоид характеризуется тремя величинами: а – большая полуось, в – малая полуось,
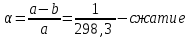.Эллипсоид ориентируется в теле Земли определенным образом. Постановлением Совета министров СССР в апреле 1946 года в нашей стране для геодезических работ принят эллипсоид Красовского Ф.Н. Его размеры:
а=6378245 м, в=6356863 м.
Эллипсоид, относительно которого ведутся все геодезические работы в данной стране, называется референц-эллипсоид.
4. Для решения многих практических задач достаточно за фигуру Земли принять шар с радиусом R=6371 км.
2
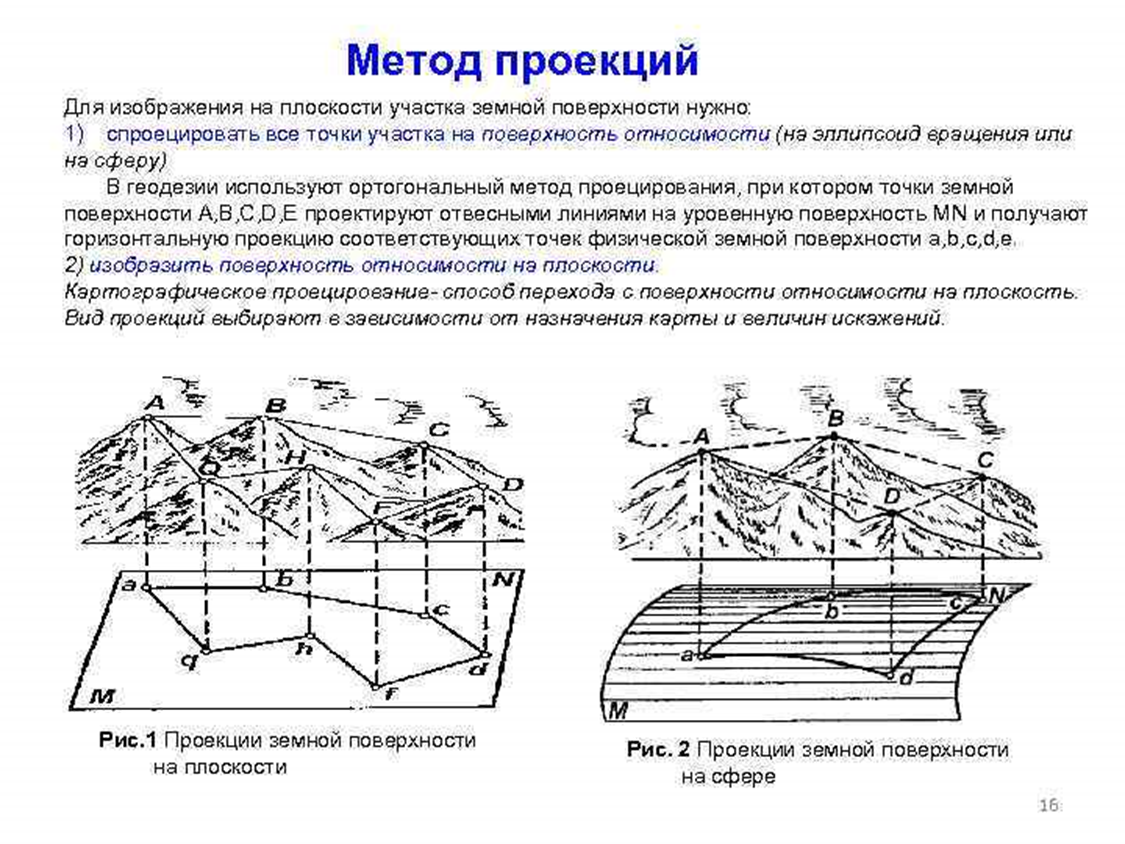. Метод проекций в геодезии. Абсолютные и условные отметки точек.Абсолютная отметка — отметка, которую измеряют от уровня Балтийского моря(Кронштадтского футштока (горизонтальной черты на медной пластине, прикрепленной к устою моста в г. Кронштадте))
Условной отметкой - называют высоту точки над какой – либо условной уровенной поверхностью
3.Системы координат в геодезии (географическая, прямоугольная, полярная)
Положение точек на карте или плане определяется координатами. Наиболее употребительны географические, прямоугольные и полярные координаты.
Географическими координатами точки являются её широта и долгота. Счет широт ведётся от экватора к северу и югу от 0 до 90о, а счет долгот – от Гринвичского меридиана к востоку и западу от 0 до 180о.
С
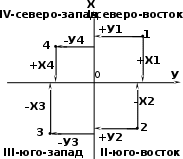истему плоских прямоугольных координат образуют две взаимно перпендикулярные линии – ось абсцисс Х и ось ординат У. Четверти нумеруются по ходу часовой стрелки и имеют своё название: I четверть – «северо-восток» (СВ), II четверть – «юго-восток» (ЮВ), III четверть – «юго-запад» (ЮЗ), IV четверть – «северо-запад» (СЗ). Положение точки определяется координатами Х и У , знаки которых зависят от четверти, в которой находится точка.Полярную систему координат формирует некоторая фиксированная точка О – полюс и некоторый фиксированный луч ОХ' – полярная ось.
В этом случае полярными координата-ми точки Р являются: S – полярный ради-ус и β – полярный угол.
(радиусом – вектором) rа, равным горизонтальному расстоянию от полюса до данной точки, и абсолютной отметкой На
4.Зональная система координат Гаусса-Крюгера
Все современные карты страны составлены в зональной системе плоских прямоугольных координат Гаусса-Крюгера. Отличительной особенностью зональной системы координат являются следующие моменты:
1. Поверхность земного эллипсоида делят на зоны шириной 6. Всего получают 360 : 6 = 60 зон. Нумерация зон ведется от Гринвича на восток. Территория России простирается с 4 по 32 зону.
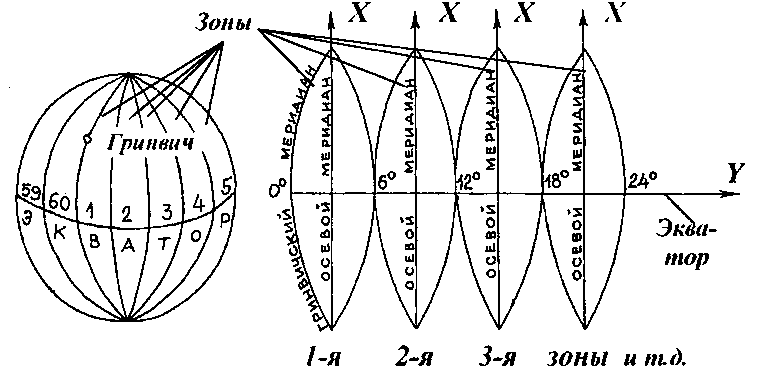
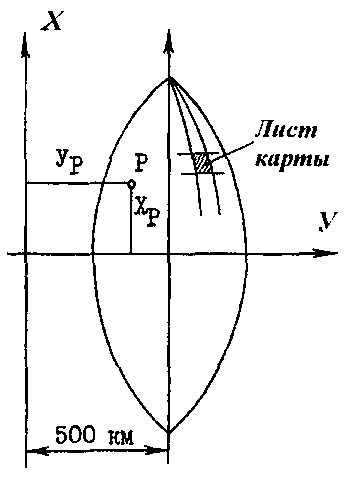
2. Каждая зона проектируется на плоскость таким образом, чтобы экватор и осевой меридиан зоны изобразились в виде прямых линий. Осевой меридиан принимается за ось Х, а экватор – за ось У.
3. Начало координат для всех точек отдельной зоны выбирается в точке пересечения осевого меридиана с экватором. Для территории России все абсциссы Х положительны, а ординаты У могут быть как положительные, так и отрицательные.
5.Ориентирование; азимуты истинные и магнитные, дирекционные углы и румбы.
Ориентировать линию – значит определить её направление относительного истинного, осевого или магнитного меридиана.
Истинным азимутом называется горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до линии местности.
Магнитный азимут АМ– это горизонтальный угол, отсчитываемый по
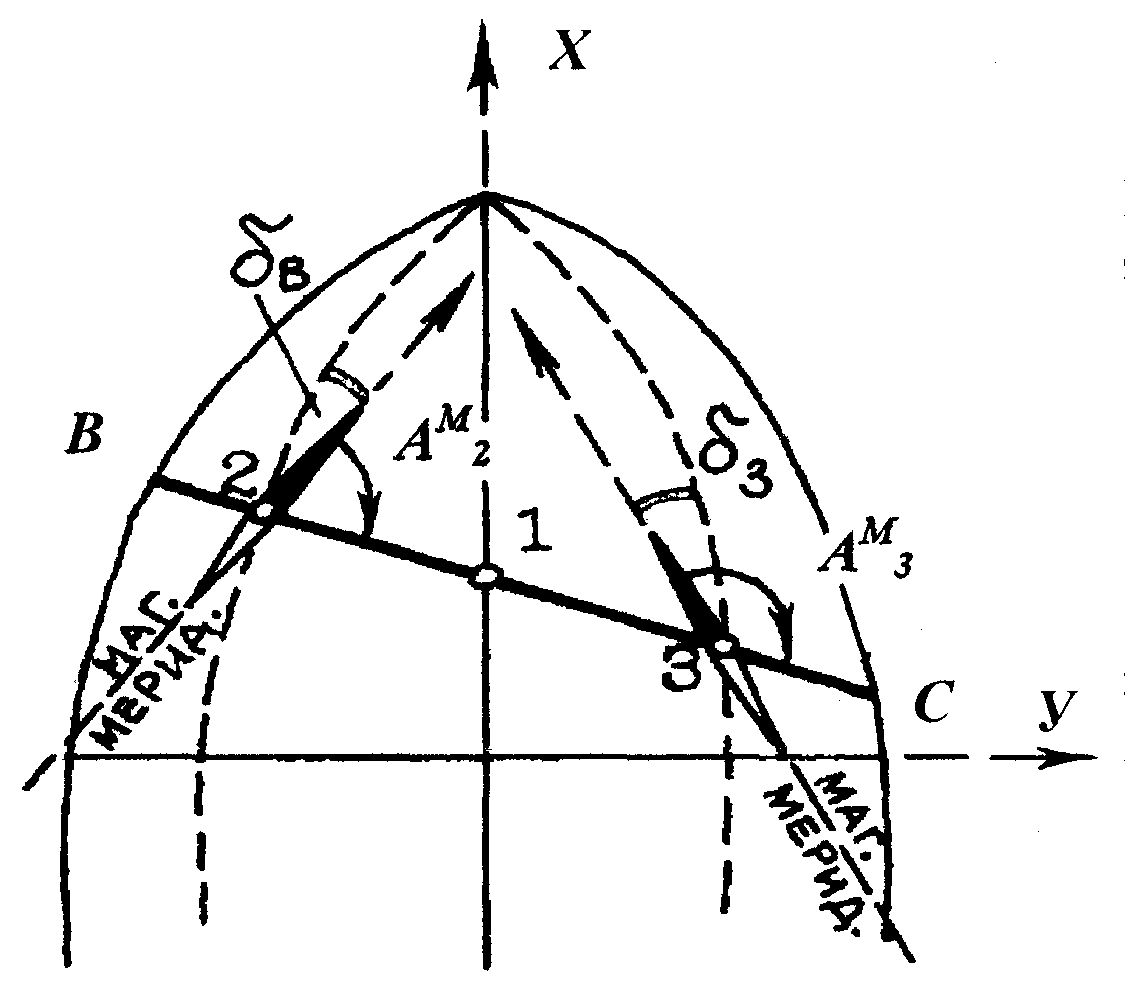
ходу часовой стрелки от северного направления магнитного меридиана до направления данной линии.
Угол между истинным и магнитным меридианами называется склонением магнитной стрелки δ , отсюда:
А2 = АМ2 + δвост ,
А3 = АМ3 – δзап .
На территории страны δ колеблется от 0о до ±15о .
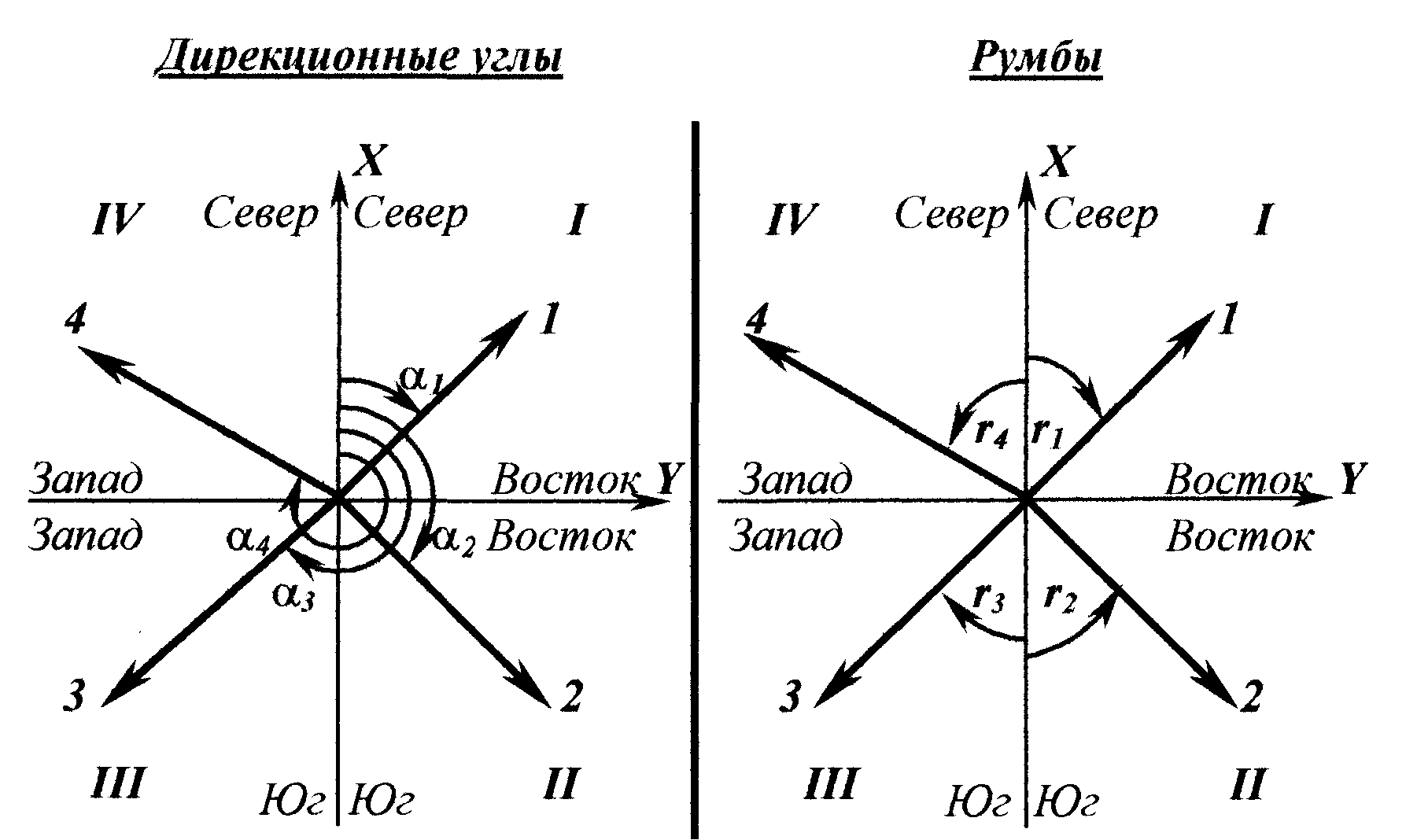
Дирекционным углом называется горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления осевого меридиана до линии местности.
Румбом называется острый горизонтальный угол r, отсчитываемый от ближайшего (северного или южного) направления осевого до направления данной линии. Румбы могут изменяться только в пределах от 0о до 90о
6.Ориентирование;связь прямых и обратных азимутов, дирекционных углов и румбов.
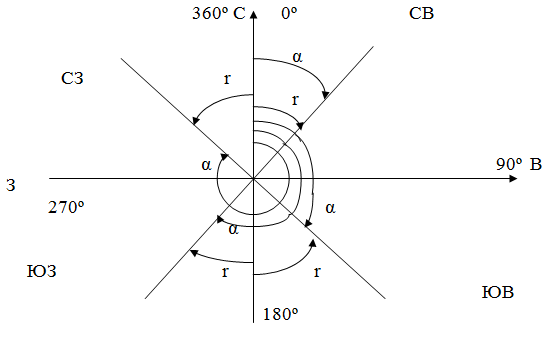
От азимутов и дирекционных углов можно переходить к румбам и обратно
СВ: r=α
ЮВ: r=180˚-α
ЮЗ: r=α-180˚
СЗ: r=360˚-α.
Если направление линии MN с точки M на точку N считать прямым, то NM будет обратным направлением той же линии. В соответствии с этим угол А1 является прямым азимутом MN в точке М, а А2 – обратным азимутом той же линии в точке N.
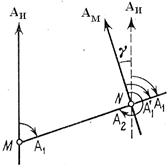
Как следует из рисунка зависимость между прямым и обратным азимутами линии MN определится выражением
А2=А1+180º+γ (γ – угол между истинными меридианами двух точек или угол между северными концами истинного и осевого меридиана. Сближение между углами бывает восточным и западным.)
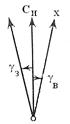или в общем случаеАобр=Апр
180º
γ7.Связь дирекционных углов и горизонтальных углов полигона
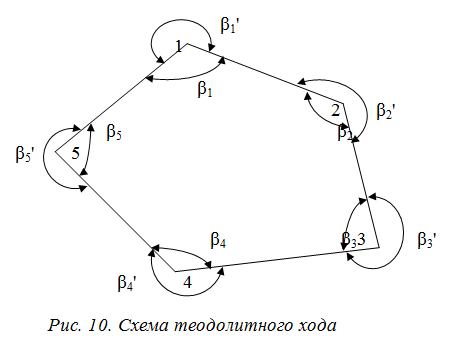
Ломаная линия с закрепленными на местности точками излома и с измеренными длинами сторон и горизонтальными углами называется полигоном. Полигоны могут быть разомкнутые и замкнутые . Точки полигона закрепляют временными знаками – деревянными кольями.β1, β2…-внутренние углы – правые; β1´, β2´…- внешние углы – левые.
Зная дирекционный угол одной стороны полигона, можно всегда вычислить по горизонтальным углам дирекционные углы всех остальных сторон.
α1-2 – дано, β1, β2…-измерены.
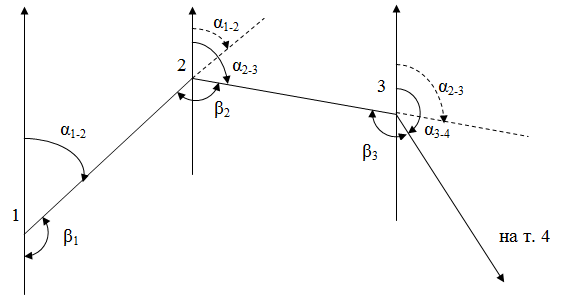
Из рисунка 11 видно, что α2-3= α1-2 +180˚ - β1
α3-4= α2-3 +180˚ - β2
αn= αn-1 +180˚ - βn - формула для правых углов.
Так как βправ.=360˚-β´лев., то для левых углов αn= αn-1 + βn´-180˚.
8. Прямая и обратная геодезические задачи
-
Прямая геодезическая задача применяется при вычислении координат в теодолитном ходе. -
Обратная геодезическая задача применяется в тех случаях, когда по известным координатам 2-х точек определяют расстояние между ними и дирекционный угол линии.
По координатам начальной точки линии 1 вычислить координаты конечной точки этой линии 2 , зная её направление α1-2 и горизонтальное проложение d1-2 .
Дано: Х1 , У1 , α1-2 , d1-2 .
Найти: Х2 , У2 .
Из решения прямоугольного треугольника (заштрихован) вычисляем приращения координат Δх1-2 и Δу1-2 :
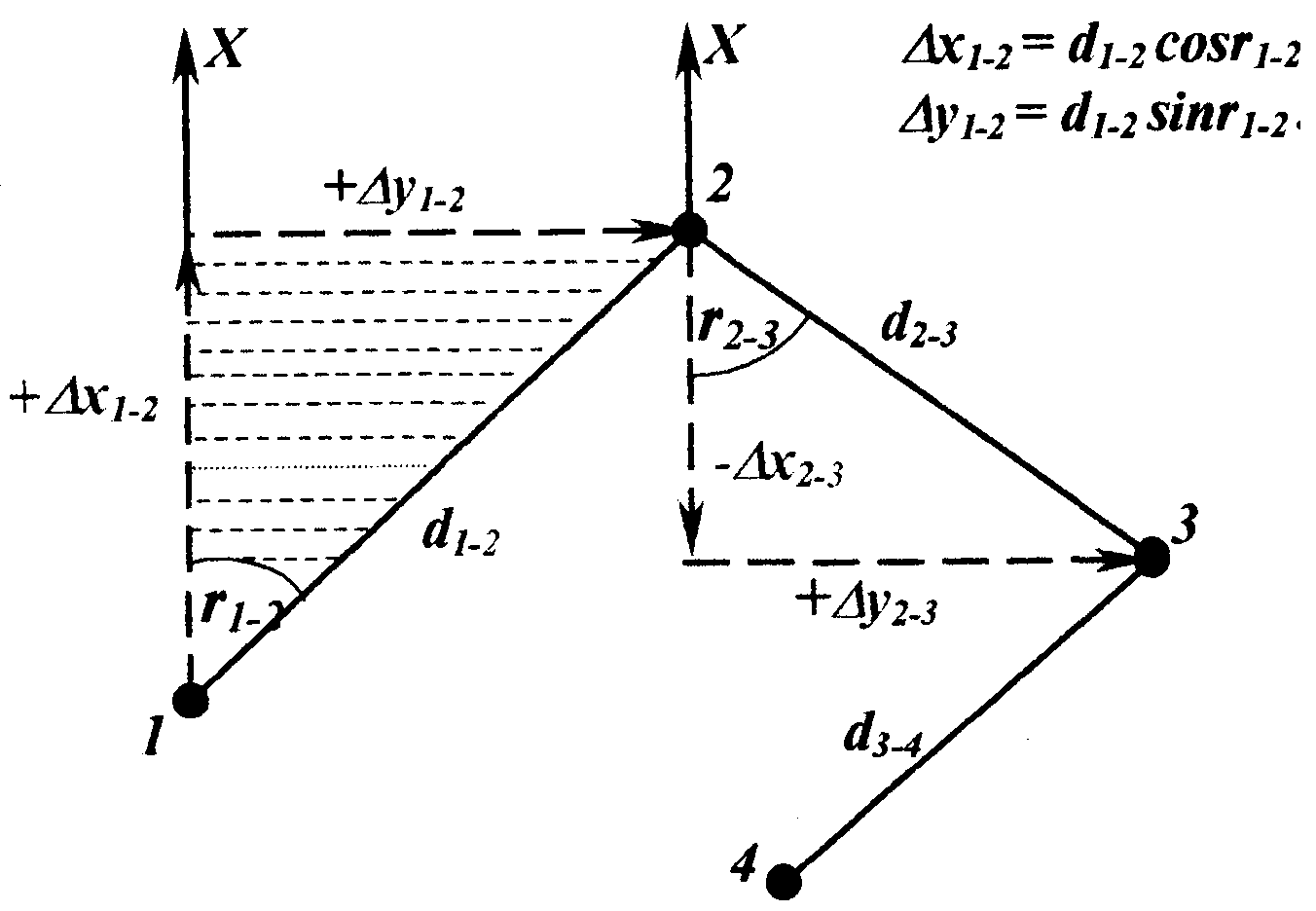
Координата конечной точки линии равна координате начальной точки этой линии плюс или минус соответствующее приращение координат между этими точками:
Х2 = Х1 + Δх1-2 ,
У2 = У1 + Δу1-2 .
Зная координаты точки 2 , можно вычислить координаты точки 3, если известен дирекционный угол α2-3 и горизонтальноепроложениеd1-2 и т. д.
Как видно из рисунков, знаки приращений координат зависят от названия румба. Так, если румб стороны 1–2 имеет название СВ, то и Δх1-2 и Δу1-2 будут со знаком «плюс». Для стороны 2–3 (ЮВ) знаки приращений –Δх2-3 и +Δу2-3. Для стороны 3–4 (ЮЗ) оба приращения со знаком «минус». И, наконец, для стороны 4–1 (СЗ) имеем +Δх4-1 и–Δу4-1 .
Обратная геодезическая задача заключается в вычислении дирекционного угла и горизонтального проложения линии, по известным координатам ее начальной и конечной точек.
По известным координатам начальной 1 и конечной 2 точек линии вычислить её направление α1-2 и горизонтальное проложение d1-2 . В нашем предыдущем примере (см. заштрихованный треугольник) задача решается в следующей последовательности:
1. Вычисляют приращения координат стороны 1–2, вычитая из координат конечной точки 2 координаты начальной точки 1, то есть:
Δх1-2 = Х2 –Х1 , Δу1-2= У2 – У1 .
2. По знакам приращений координат определяют название румба, а по отношению Δу/Δх = tgr1-2 находят значение румба.
3. По величине и названию румба находят дирекционный угол α1-2 данной линии (см. таблицу на стр. 19).
4. Вычисляют величину горизонтального проложения :d1-2 = Δх/cosr или d1-2 = Δу/sinr. По обеим формулам должны получить два абсолютно одинаковых значения , что является контролем решения обратной геодезической задачи. С обратной геодезической задачей студенты встречаются при выполнении лабораторной работы «Подготовка разбивочных данных».