Файл: Экспериментальные данные для варианта 5 (Табл. 1).docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 31

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

  1. Экспериментальные данные для варианта 5 (Табл. 1):

i
1
2
3
4
5
6
7
8
9
10

xi
0,04
0,05
0,09
0,11
0,15
0,18
0,19
0,20
0,21
0,33


































i
11
12
13
14
15
16
17
18
19
20

xi
0,42
0,44
0,44
0,52
0,56
0,58
0,61
0,61
0,63
0,67


































i
21
22
23
24
25
26
27
28
29
30

xi
0,69
0,69
0,70
0,71
0,72
0,72
0,77
0,80
0,83
0,98


































i
31
32
33
34
35
36
37
38
39
40

xi
0,99
1,04
1,07
1,09
1,20
1,38
1,41
1,55
1,60
1,83

Табл. 1. Экспериментальные данные

  1. По заданным ЭД построим вариационный ряд (Табл. 2) и статистический ряд (Табл. 4). Для этого вычислим частоты Ni и относительные частоты Ni=Ni/N (Табл. 3)

i
1
2
3
4
5
6

xi
0,04
0,33
0,62
0,91
1,2
1,49

Табл. 2. Вариационный ряд.

i
1
2
3
4
5
6

xi
0,04
0,33
0,62
0,91
1,2
1,49

ni
9
9
11
5
3
3

ni=ni/n
0,225
0,225
0,275
0,125
0,075
0,075

Табл. 3. Вычисление частот Ni и относительных частот Ni=Ni/N для вариационного ряда.

xi
0,04-0,33
0,33-0,62
0,62-0,91
0,91-1,2
1,2-1,49
1,49-1,78

zi
0,776
0,776
0,948
0,431
0,259
0,259

Табл. 4. Статистический ряд.

Затем построим таблицу плотности распределения (Табл. 5) и функцию распределения (Формула 1). Затем построим график функции распределения (Рис. 1).

xi
0,04-0,33
0,33-0,62
0,62-0,91
0,91-1,2
1,2-1,49
1,49-1,78

ni
0,225
0,225
0,275
0,125
0,075
0,075

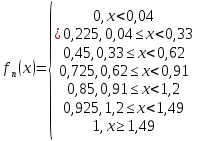– функция распределения (Формула 1)

Табл. 5 Плотность распределения



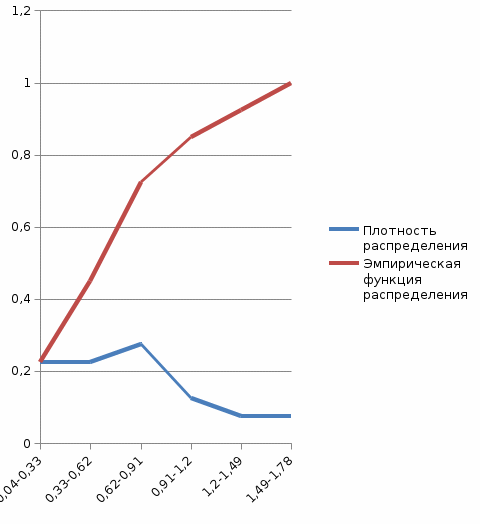
Рис. 1. Графики плотности распределения и эмпирической функции распределения по разрядам статистического ряда.

На рисунке 1 представлены графики плотности распределения и эмпирической функции распределения, построенные с помощью табл. 5 и табл. 3. На рисунке видно, что плотность распределения можно аппроксимировать логарифмически-нормальным законом распределения.

  1. Теперь перейдем к оценке моментов распределения.

 
1
2
3
4

η
0,714
0,694
0,806
1,042

μ
0,714
0,185
0,046
0,086

Табл. 6. Оценки четырех начальных (η) и центральных (μ) моментов по сгруппированным данным

σ
0,430

β1
0,126

β2
2,521

Табл. 7. Среднеквадратическое отклонение (σ), коэффициенты асимметрии (β1) и эксцесса (β2) для сгруппированных данных

 
1
2
3
4

η
0,695
0,682
0,804
1,068

μ
0,695
0,199
0,053
0,112

Табл. 8. Оценки четырех начальных (η) и центральных (μ) моментов по не сгруппированным данным

σ
0,446

β1
0,157

β2
2,815

Табл. 9. Среднеквадратическое отклонение (σ), коэффициенты асимметрии (β1) и эксцесса (β2) для не сгруппированных данных

В табл. 6 и 8 представлены вычисленные оценки четырех начальных и центральных моментов, по таблицам видно, что при использовании сгруппированных и не сгруппированных данных получились похожие значения с относительно небольшой погрешностью. Также в табл. 7 и 9 представлены вычисленные СКО, коэффициенты асимметрии и эксцесса для сгруппированных и не сгруппированных данных, которые тоже близки по своим значениям. Из табл. 6 – 9 можно сделать вывод, что в целях удобства обработки и хранения сведений можно прибегать к группированию ЭД в интервалы.

Вывод

В процессе выполнения контрольной работы были произведены расчеты для заданных экспериментальных данных, построение вариационного и статистического рядов для него, построение гистограмм эмпирической функции распределения и функции плотности распределения, а также вычислены оценки моментов и квантилей распределения. Для данного набора данных (вариант 5) можно сделать вывод, что плотность распределения стоит аппроксимировать логарифмически-нормальным законом распределения. А
также основной вывод в том, что в целях удобства обработки и хранения сведений можно прибегать к группированию ЭД в интервалы.

Список литературы

  1. Ходасевич Г.Б., Пантюхин О.И., Ногин С.Б. Планирование эксперимента и обработка экспериментальных данных на ЭВМ. Ч. 1. Обработка экспериментальных данных на ЭВМ: учебное пособие; СПбГУТ.- СПб., 2014. – 88с.

  2. Ходасевич Г.Б., Пантюхин О.И., Ногин С.Б. Планирование эксперимента и обработка экспериментальных данных на ЭВМ. Ч. 2. Планирование эксперимента: учебное пособие; СПбГУТ.- СПб., 2014. – 88с.

  3. Статья в электронной библиотеке Википедия «Распределение вероятностей» https://ru.wikipedia.org/wiki/Распределение_вероятностей

  4. Статья в электронной библиотеке Википедия «Логнормальное распределение» https://ru.wikipedia.org/wiki/Логнормальное_распределение

Смотрите также файлы