Файл: Задача Пусть A0, 1, . На ленте в ячейках находятся символы из алфавита в следующем порядке 0011011. каретка находится над первым символом. Необходимо составить программу, которая заменит 0 на 1, 1 на 0 и вернет каретку в первоначальное положение.docx
Добавлен: 09.11.2023
Просмотров: 101
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Машина Тьюринга представляет собой бесконечную ленту, поделенную на ячейки, и каретку (считывающе-печатающее устройство), которая движется вдоль ленты.
Таким образом Машина Тьюринга формально описывается набором двух алфавитов:
A={a1, a2, a3, …, an} — внешний алфавит, служит для записи исходных данных
Q={q1, q2, q3,…, qm} — внутренний алфавит, описывает набор состояний считывающе-печатного устройства.

Машина Тьюринга
Каждая ячейка ленты может содержать символ из внешнего алфавита A = {a0,a1,…,an} (В нашем случае A={0, 1})
Допустимые действия Машины Тьюринга таковы:
1) записать какой-либо символ внешнего алфавита в ячейку ленты (символ, бывший там до того, затирается)
2) сместиться в соседнюю ячейку
3) сменить состояние на одно из обозначенных символом внутреннего алфавита Q
Машина Тьюринга — это автомат, который управляется таблицей.
Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q = {q0,q1,…,qm}. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние, попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей
- символ из алфавита A
- направление перемещения: «>» (вправо), «<» (влево) или «.» (на месте)
- новое состояние автомата

В приведенной выше таблице алфавит A ={0, 1, _} (содержит 3 символа), а внутренний алфавит Q={q1, q2, q3, q4, q0}, q0 — состояние, заставляющее каретку остановиться.
Рассмотрим несколько задач решением.
Задача 1. Пусть A={0, 1, _}. На ленте в ячейках находятся символы из алфавита в следующем порядке 0011011. каретка находится над первым символом. Необходимо составить программу, которая заменит 0 на 1, 1 на 0 и вернет каретку в первоначальное положение.
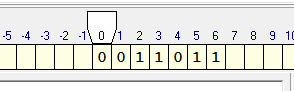
Теперь определимся с состояниями каретки. Я называю их — «желания каретки что-то сделать».
q1) Каретка должна пойти вправо: если видит 0 меняет его на 1 и остается в состоянии q1, если видит 1 — меняет его на 0 и остается в состоянии q1, если видит _ — поворачивается назад на 1 ячейку «желает что-то другое», т.е переходит в состояние q2. Запишем наши рассуждения в таблицу исполнителя. Синтаксис смотрите в справке к программе)
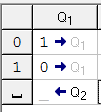
q2) Теперь опишем «желание каретки» q2. Мы должны вернуться в первоначальное положение. Для этого: если видим 1 оставляем ее и остаемся в состоянии q2 (с тем же желанием дойти до конца ряда символов); если видим 0 — оставляем его и продолжаем двигаться влево в состоянии q2; видим _ — сдвигается вправо на 1 ячейку. Вот вы оказались там, где требуется в условии задачи. переходим в состояние q0.
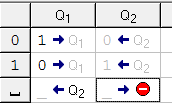
Посмотреть работу программы можно на видео:
Задача 2. Дано: конечная последовательность 0 и 1 (001101011101). Необходимо выписать их после данной последовательности, через пустую ячейку, а в данной последовательности заменить их на 0. Например:
Из 001101011101 получим 000000000000 1111111.
Как видите, семь единиц записались после данной последовательности, а на их местах стоят нолики.
Приступим к рассуждениям. Определим, какие состояния необходимы каретке и сколько.
q1) увидел 1 — исправь на нолик и перейди в другое состояние q2 (новое состояние вводится, чтобы каретка не поменяла на нули все единицы за один проход)
q2) ничего не менять, двигаться к концу последовательности
q3) как только каретка увидела пустую ячейку, она делает шаг вправо и рисует единичку, если она видит единичку — то движется дальше, чтобы подписать символ в конце. Как только нарисовал единицу, переходим в состояние q4
q4) проходим по написанным единицам, ничего не меняя. Как только доходим до пустой ячейки, разделяющей последовательность от единиц, переходим в новое состояние q5
q5) в этом состоянии идем начало последовательности, ничего не меняя. Доходим до пустой ячейки, разворачиваемся и переходим в состояние q1
Состояние q0 каретка примет в том случае, когда она пройдет в состоянии q1 до конца данной последовательности и встретит пустую ячейку.
Получим такую программу:
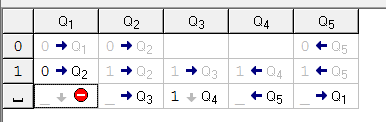
Машина Тьюринга
Представим себе ленту произвольной длины. Лента вертикальными черточками разделена на равные участки, называемые ячейками. В каждой ячейке может быть записан один символ (цифра, буква, знак препинания, математический символ и прочее). Некий образец такой ленты изображен на рис.1

Рис. 1 Входное слово на ленте для сложения чисел 5 и 3
Примечание: греческая буква «ламбда» у нас будет обозначать пустую ячейку, в которой никакой символ не записан.
Последовательность символов на ленте будем называть записью или словом. В нашем примере запись предлагает решить элементарную задачу – сложить два числа. Под лентой размещается так называемая головка ( положение ее у нас показано символом состояния машины – в данном случае символ q0), способная читать определенный символ в ячейке, или, стерев старый, записать в ячейку новый. Также головка способна перемещаться вдоль ленты на одну позицию за один такт работы машины Тьюринга влево или вправо. Можно считать головку неподвижной, а за один такт на одну ячейку смещается лента (в этом случае влево, вправо меняются местами). Кроме того машина Тьюринга (далее - МТ) должна иметь еще одно принципиальной важности устройство – устройство управления. Назначение устройства управления – задать машине правила записи-стирания символов на ленте, правила движения головки (ленты), а также правила изменения состояния машины. Создать (запрограммировать) МТ, фактически означает создать ее устройство управления.
Устройство управление – это никакое ни «железо», ни «электроника». Это – нарисованная (напечатанная) на листе бумаги прямоугольная таблица. Мы уже уточнили, что представленную на рис.1 запись можно трактовать как исходное задание машине решить задачу. Разработать таблицу управления машины, если задание задано в общем виде, т.е. вместо цифр 5 и 3 будут любые цифры или числа десятичной системы счисления уже достаточно трудно. Поэтому для примера изобразим таблицу управления МТ только для конкретной записи, изображенной на рис.1. Такая таблица может выглядеть так, как показано на рис.2.
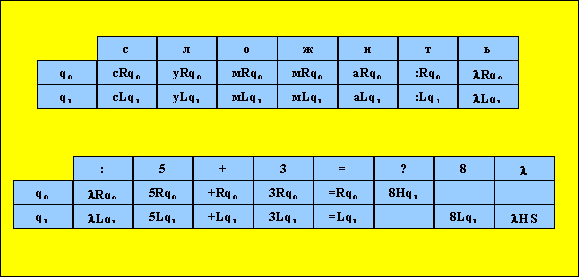
Рис.2 «Устройство управления» машины Тьюринга для сложения чисел 5 и 3
Примечание: Таблица для удобства размещения на странице разделена на две части – верхнюю и нижнюю. Для восстановления ее единства необходимо нижнюю часть «приклеить» справа к верхней.
Как понимать эту таблицу? Пусть до начала работы головка находится, как показано на рис.1, под буквой «с», а машина пребывает в начальном состоянии, обозначенным символом q0. Смотрим клетку таблицы на пересечении строки с буквой «с» и столбца с символом q0. В этой клетке записана последовательность (тройка) символов сRq0. Тройка символов – это команда МТ. В данном конкретном случае эту тройку следует понимать так: машина в ячейке, под которой расположена головка, сохранит букву «с» (точнее – сотрет букву «с» и вновь запишет букву «с»); оставит машину в прежнем состоянии q0 и сдвинет головку (пусть движется головка) на один шаг вправо (буква R от слова Right – вправо).
В начале следующего такта головка теперь расположена под ячейкой с буквой «л». Смотрим в таблице строку с буквой «л» и столбец с символом q0, т.к. машина по прежнему находится в состоянии q0. На их пересечении – команда (тройка) уRq0. Нам уже понятно, что по этой команде буква «а» стирается, на ее место записывается буква «у», машина по прежнему остается в состоянии q0, а головка вновь сдвигается на один шаг вправо.
Читатель теперь без труда, самостоятельно, может проследить как будет работать машина до момента, когда головка прочитает с ленты символ «?». Очевидно, что вместо знака вопроса она запишет цифру 8. Следует только обратить внимание, что машина теперь перейдет в состояние q1, а головка никуда не сдвинется (буква «H» от слова Halt – стоять). Теперь по таблице легко проследить, что головка, ничего на ленте не изменяя, будет двигаться влево (буква «L» от слова Left – влево) до тех пор, пока не окажется под пустой ячейкой (символ «ламбда»). Здесь видно, что головка остановится и машина перейдет в состояние S (от слова Stop – останов).
Читатель может спросить – зачем нужно было после получения ответа (число 8) двигать головку вдоль всей ленты влево: результат же был получен раньше? В самом деле, можно было без этого обойтись, но для более строгой (в математическом смысле) трактовки работы МТ целесообразно головку в конце работы помещать относительно ленты там, где она была вначале. Наиболее внимательные обязательно заметят, что это требование нашей машиной нарушено: головка на одну позицию оказалась левее исходной. Исправить этот «недостаток» легко: достаточно команду-тройку "ламбда"HS последней строки таблицы ( на рис.2) заменит командой-тройкой "ламбда"RS. Слово-результат после окончания вычислений показано на рис.3.

Рис.3 Слово на ленте после окончания вычислений
В машине Тьюринга всевозможные математические (и не только математические) задачи оказались сведенными к сколь угодно длинной череде одних и тех же простейших операций: считать-записать символ, сдвинуть головку и перевести машину из одного состояния в другое. Всё!!! Это и есть общее, единое для любых, самых разных вычислений. Поэтому, в более строгой форме мы можем заявить – задача вычислима (существует алгоритм решения задачи), если существует машина Тьюринга, решающая эту задачу. В данном случае не важно – идет ли речь о подсчете на калькуляторе стоимости покупок в магазине, или расчете в компьютере траектории полета космического корабля. Разумеется, никто не будет использовать машину Тьюринга для решения даже самых простых задач. Неоспоримая заслуга Алена Тьюринга состоит в том, что он нашел единый (и достаточно наглядный) способ определения вычислимости.
Если в начале работы считывающе-записывающая головка занимала определенное положение (у нас в примере, допустим, под первым символом входного слова), если в процессе работы машина «прочитала» входное слово полностью (т.е. обошла все символы входного слова, кстати, можно и по нескольку раз), если останов машины произошел в исходном положении головки, то говорят – задача решена, существует алгоритм ее решения, проблема вычислима.