Файл: Задача Д1 Материальная точка массой m 7 (кг) движется в горизонтальной плоскости хОу под действием силы f fхi fуj, где fх 12sin (7t) (Н) fу 74cos (7t) (Н), (рисунок 1)..docx
Добавлен: 09.11.2023
Просмотров: 260
Скачиваний: 21
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
При решении задач введены обозначения:
Г – количество букв в имени;
П – количество букв в фамилии; если больше 9-ти, то берется последняя цифра;
С – количество букв в отчестве
Г=7; П=7; С=9
Задача Д1
Материальная точка массой m = 7 (кг) движется в горизонтальной плоскости хОу под действием силы F = FХ·i + FУ·j,
где FХ = 12·sin (7·t) (Н); FУ = 74·cos (7·t) (Н), (рисунок 1).
Определить уравнение движения точки, если начальные условия:
x0 =10(м); y0 = 11 (м); VХ0 = 10 (м / с); VУ0 = 0 (м / с).
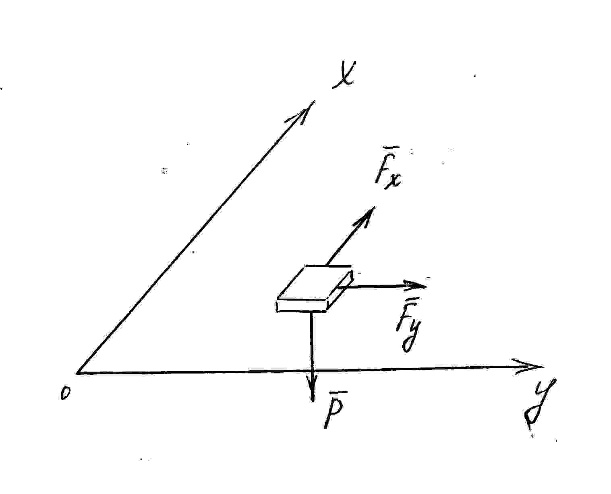
Рисунок 1
Решение.
1. Рассмотрим движение точки в плоскости ХОУ. Изображаем материальную точку (в произвольном положении) и действующие на него силы
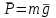 ,
, 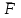 . Проводим оси ОХ, ОУ. Составляем дифференциальные уравнение движения груза в проекции на эти оси:
. Проводим оси ОХ, ОУ. Составляем дифференциальные уравнение движения груза в проекции на эти оси: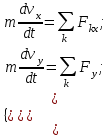 или
или 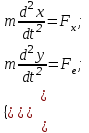 (1)
(1) где
где 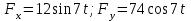
Тогда
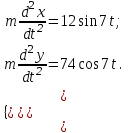
Разделяя в уравнении (1) переменные, а затем беря от обеих частей интегралы, получим
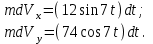
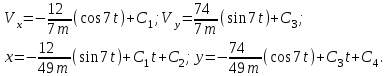
Начальные условия: при t=0;
x0 =10(м); y0 = 11 (м); VХ0 = 10 (м / с); VУ0 = 0 (м / с).
Тогда
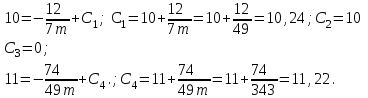
Уравнения движения примут вид:
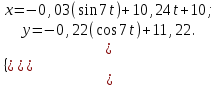
Задача Д 2
Круглая пластина радиуса R = 1,4 (м) и массой m1 = 18 (кг) вращается с угловой скоростью (-40) (с -1 ) вокруг вертикальной оси z, проходящей через точку О перпендикулярно. На пластине имеется желоб, по которому начинает двигаться точка М массой m2 = 7 (кг) по закону / АМ / = 0,7·t 2 (м).
Найти угловую скорость пластины в момент времени 1 с.
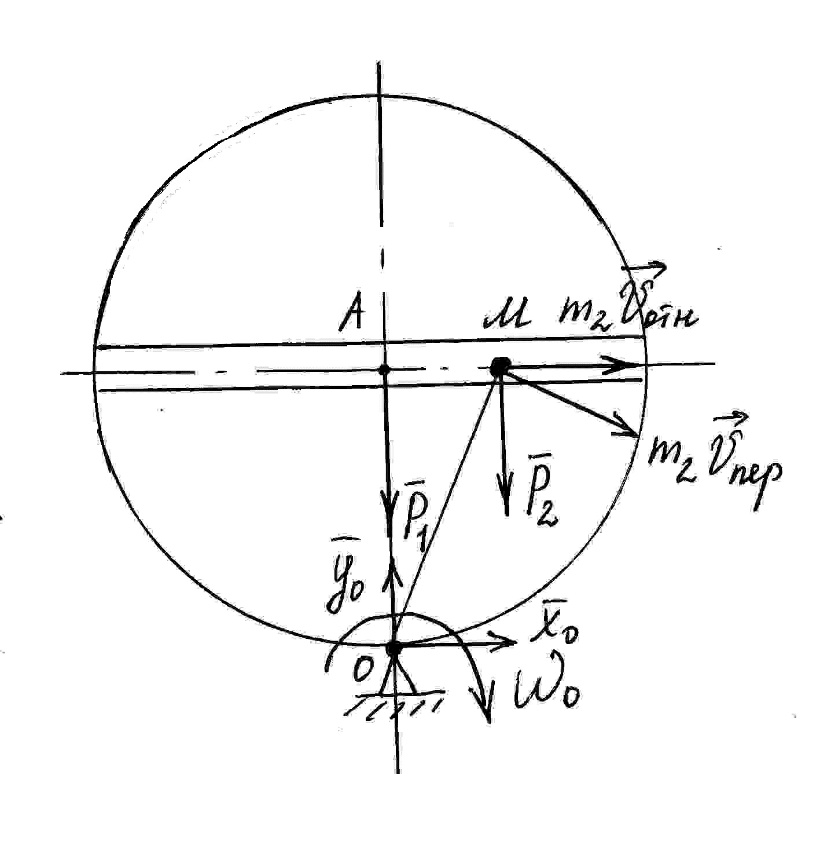
Рисунок 2
Решение.
Так как начальная угловая скорость отрицательна, направим ее по часовой стрелке и примем
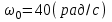
Применим теорему об изменении кинетического момента системы относительно оси z:
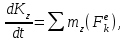 где
где 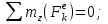
Тогда
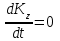
Умножим обе части на dt и интегрируя, получим
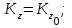
где
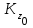 - кинетический момент механической системы в начальный момент времени.
- кинетический момент механической системы в начальный момент времени.Для рассматриваемой механической системы
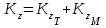 ,
, где
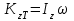 - кинетический момент пластины;
- кинетический момент пластины;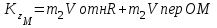 - момент количества движения точки М, так как точка совершает сложное движение.
- момент количества движения точки М, так как точка совершает сложное движение.Здесь
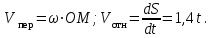
Тогда, по теореме Вариньона
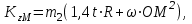
где
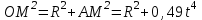
Момент инерции пластины определим по формуле Гюйгенса:
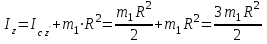 .
.Тогда
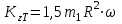
Для всей системы
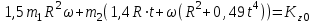 (2)
(2)Из начальных условий: при t=0;
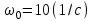 , получим
, получим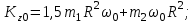
Подставляем в (2) и выражаем искомую зависимость угловой скорости от времени:
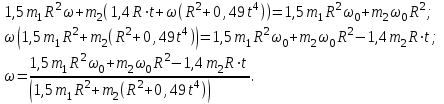
При t=1 c
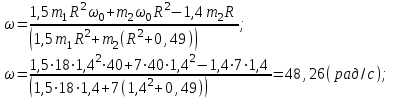
Задача Д 3
Механическая система состоит из груза 1, ступенчатых шкивов 2 и 3 и катка 4 с радиусами: r2 = 0,2 (м); R2 = 0,4 (м); г3 = 0,3 (м); R3 = 0,4 (м); R4 = 0,5 (м). Радиусы инерции 2-го и 3-го тела: i2 = 0,3 (м); i3
= 0,33 (м). Коэффициент трения груза 1 о плоскость f = 0,1; коэффициент трения качения колеса 4 равен 0,002 (м). Система начинает движение из состояния покоя в направлении, обусловленном направлением вращения моментов М4 = 49 (кН·м) (если П = 7...9).
Определить скорость груза 1 в тот момент, когда его перемещение станет равным S = 0,7 (м), если массы тел: m1 = 7 (кг); m2 = 14 (кг); m3 = 7 (кг); m4 = 63 (кг); а углы: α = 65 (град); β = 45 (град).
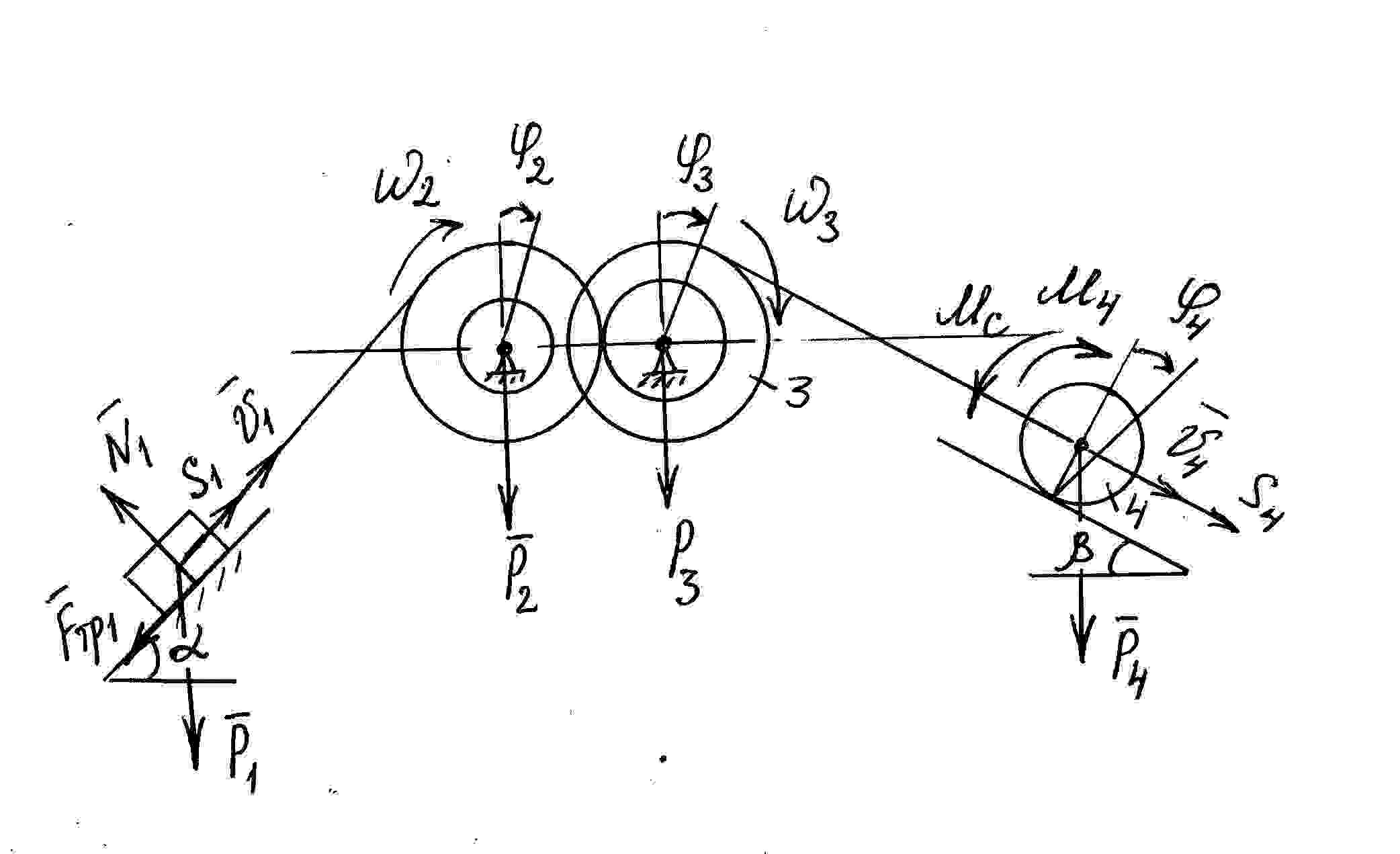
Рисунок 3
Решение.
Применим теорему об изменении кинетической энергии механической системы:
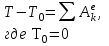
так как система начала движение из состояния покоя.
Кинетическая энергия механической системы
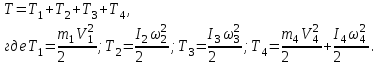 (3)
(3)Выразим
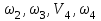 через искомую скорость груза 1 -
через искомую скорость груза 1 - 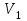 .
.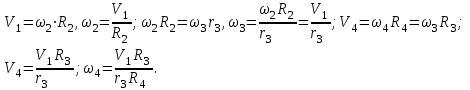
Моменты инерции тел 2, 3, 4
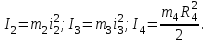
Подставим в (3) и определим кинетическую энергию системы
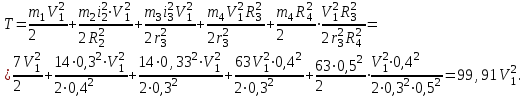
Определим сумму работ всех внешних сил:
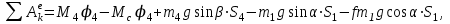
где
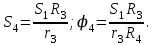
Тогда
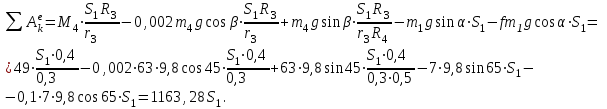
Приравняем кинетическую энергию и работу всех внешних сил, получим
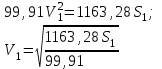
При S1=0,7м
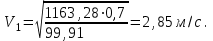
Задача Д 4
Вал, закрепленный вертикально в подпятнике А и в подшипнике В, вращается с постоянной угловой скоростью 59 (c -1 ). С валом в одной плоскости под углами α = 80 (град) и β = 55 (град) к его оси жестко соединены однородный стержень / CD / = 7 (м), массой m1 = 7 (кг) и невесомый стержень / ЕМ / = 7 (м), на конце которого закреплена материальная точка М массой m2 = 7 (кг).
Определить реакции в точках А и В, если /AС / = / CE / = / EB / = 3,5 (м).
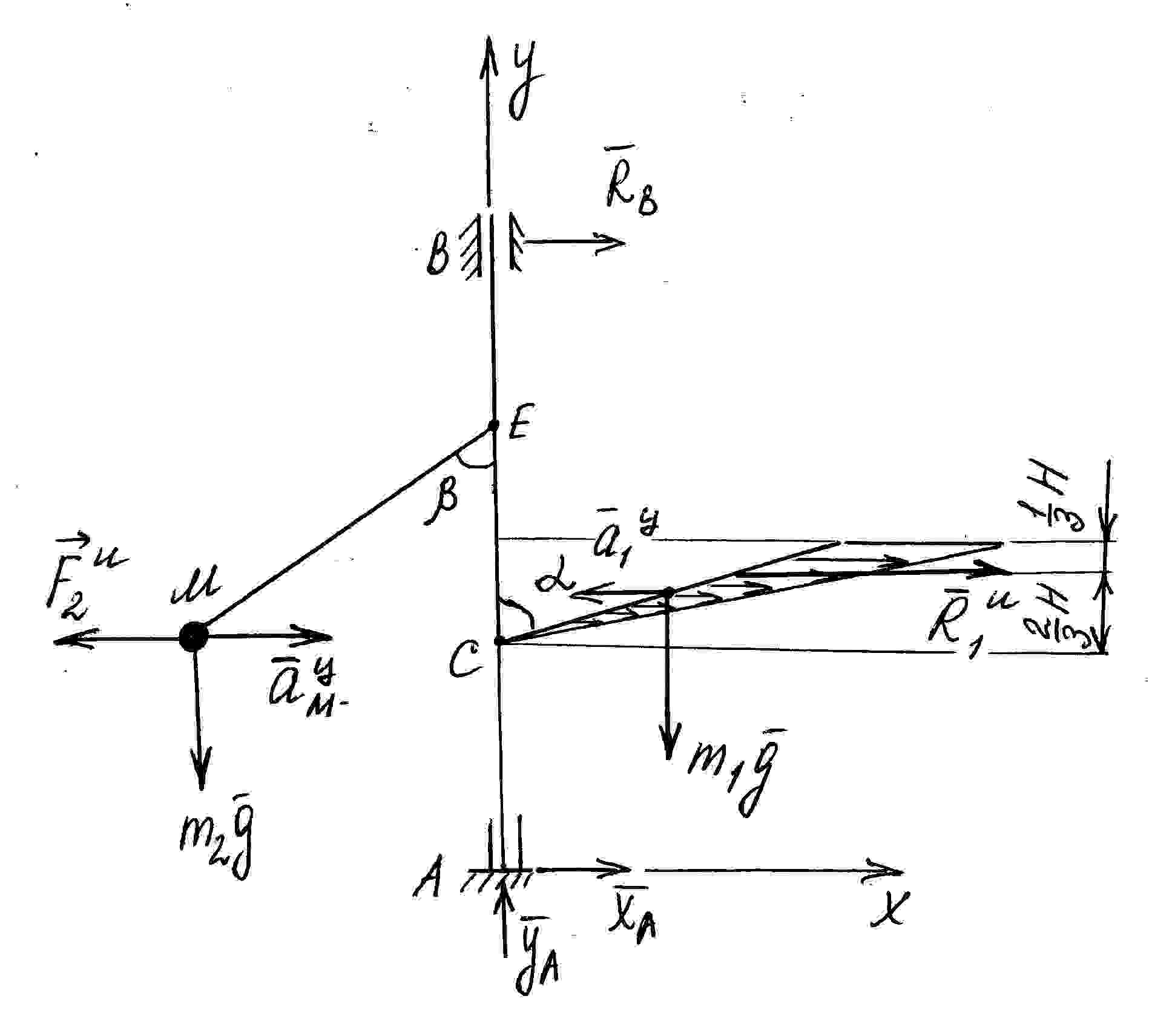
Рисунок 4
Решение.
Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом координатные оси Аху так, чтобы стержни лежали в плоскости ху и изобразим действующие на систему силы: активные силы – силы тяжести m1g, m2g и реакции связей – ХА, УА, RВ.
Согласно принципу Даламбера, присоединим к этим силам силы инерции стержня и груза, считая его материальной точкой.
Так как вал вращается равномерно, то
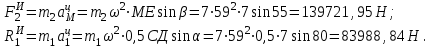
Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим три уравнения равновесия:
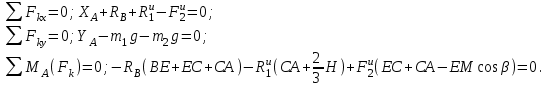
где
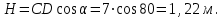
Тогда

Задача Д 5
Механизм, расположенный в горизонтальной плоскости, находится в равновесии.
Определить значение силы Р, если F1 = 15 (кН); F2 = 16 (кН); F3 = 16 (кН); М1 = 14 (кНм); М2 = 5 (кНм); α = 80 (град); β = 55 (град); χ = 55 (град); / О1A / = / AB / = / BC / = 1 (м) = / BD / =1 (м).
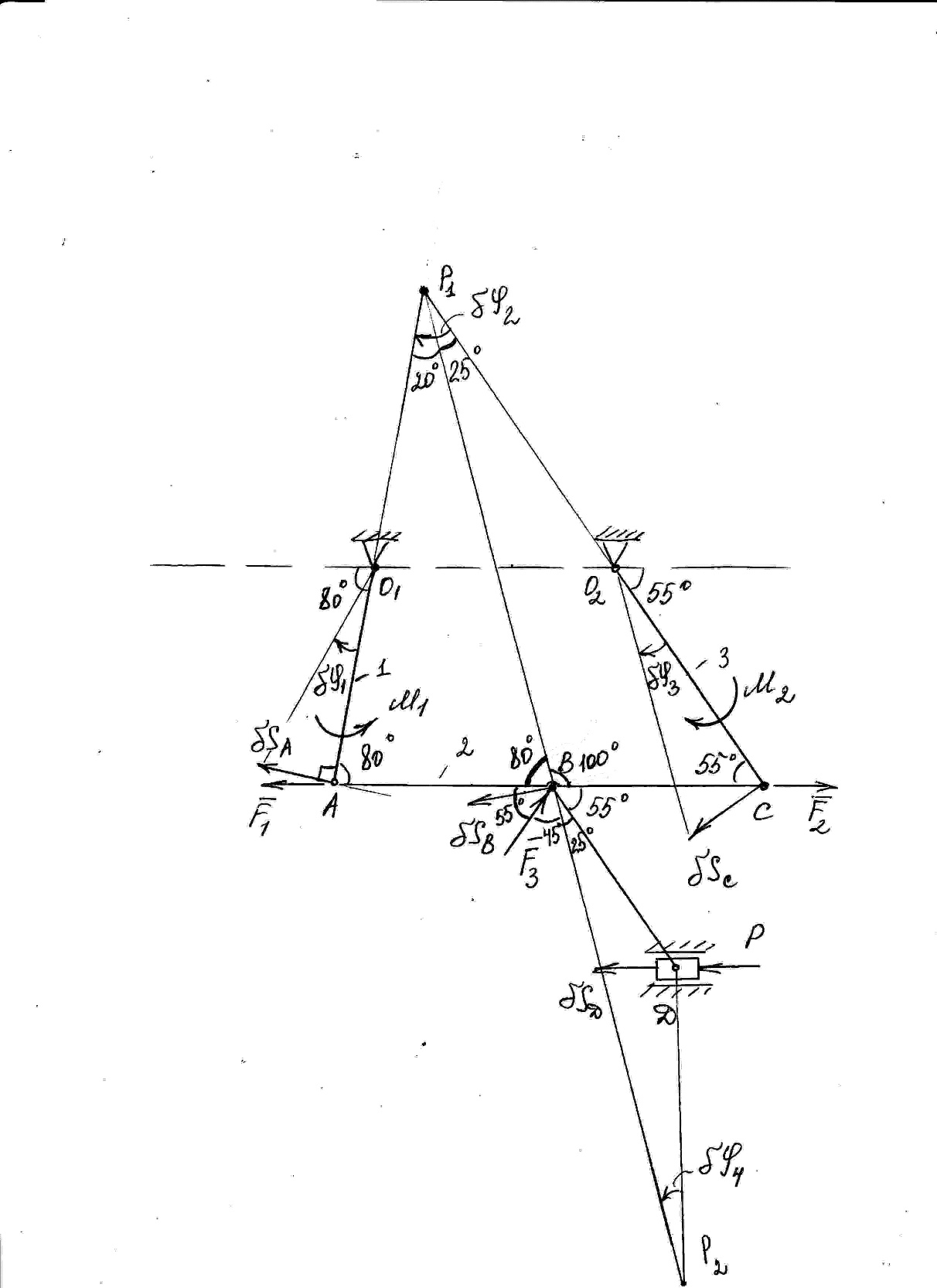
Рисунок 5
Решение.
Для решения задачи воспользуемся принципом возможных перемещений, согласно которому
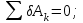
где
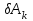 - элементарные работы активных сил на соответствующих возможных перемещениях.
- элементарные работы активных сил на соответствующих возможных перемещениях. Тогда получим уравнение
Тогда получим уравнение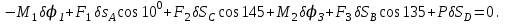 (4)
(4)Найдем зависимость между линейными и угловыми перемещениями.
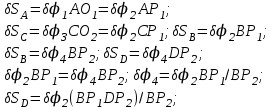
Определим все расстояния, указанные в формулах.
Из теоремы синусов
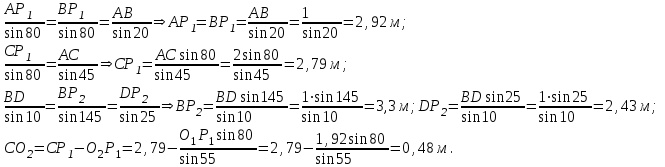 Подставим все в (4) и выразим Р.
Подставим все в (4) и выразим Р.
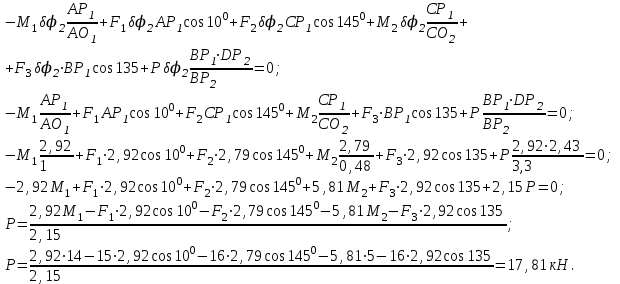
Задача Д 6
Круглое колесо радиуса R = 0,7 (м) и массой 7 (кг) катится по неподвижной горизонтальной оси без скольжения из состояния покоя. К центру колеса приложена постоянная горизонтальная сила 16Н. Коэффициент трения качения равен 0,001 (м).
Определить абсолютное ускорение центра колеса
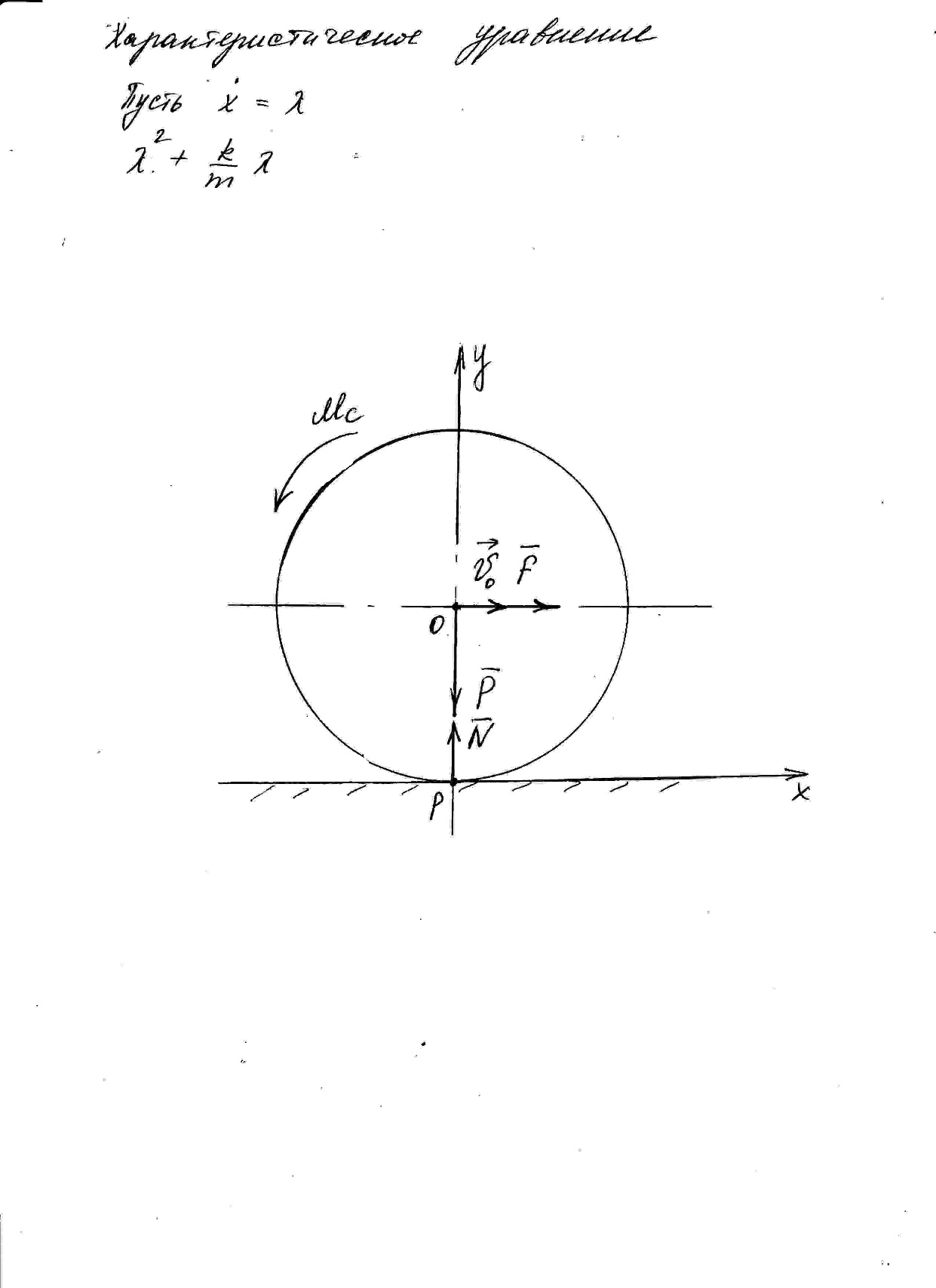
Рисунок 6
Решение.
Колесо совершает плоскопараллельное движение.
Проводим оси Рху и составляем дифференциальные уравнения плоскопараллельного движения:
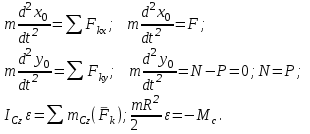
Момент сопротивления трению качения
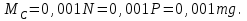
Учтем, что
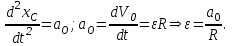
Тогда
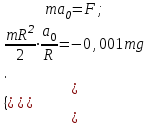
Сложим оба уравнения и получим