Файл: Отчет по контрольной работе 2 по дисциплине Теория вероятностей и математическая статистика.docx
Добавлен: 09.11.2023
Просмотров: 218
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования РФ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Томский государственный университет систем управления
и радиоэлектроники» (ТУСУР)
Кафедра автоматизированной обработки информации (АОИ)
Отчет по контрольной работе №2 по дисциплине
«Теория вероятностей и математическая статистика»
Вариант №17
Студент ФДО ТУСУР
Гр. з-422П8-5
____ Курьянович В.А.
«___»___________202_ г.
Руководитель:
Старший преподаватель
каф. АОИ ____Ю. В. Синчинова
«___»___________202_ г.
Томск 2023
Задача 1. Тема: «Нормальное распределение»
Предположим, что в течение года цена на акции некоторой компании есть случайная величина, распределенная по нормальному закону с математическим ожиданием, равным 48 у.е., и стандартным отклонением, равным 6. Определите вероятность того, что в случайно выбранный день обсуждаемого периода цена отклонится не больше чем на 7 у.е. за акцию.
Решение:
Для решения задачи необходимо использовать формулу вероятности нормального распределения:
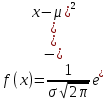
где μ - математическое ожидание, σ - стандартное отклонение.
В нашем случае μ=48, σ=6.
Так как мы ищем вероятность того, что цена отклонится не больше чем на 7 у.е., то нам нужно найти вероятность того, что цена будет находиться в интервале
[48−7;48+7]=[41;55]
Для этого необходимо вычислить две вероятности:
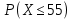
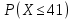
Затем найдем разность этих вероятностей:
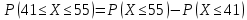
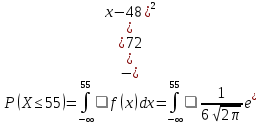
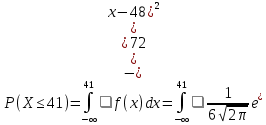
Тогда искомая вероятность равна:
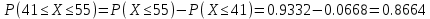
Таким образом, вероятность того, что в случайно выбранный день обсуждаемого периода цена отклонится не больше чем на 7 у.е. за акцию равна 0.8664.
Задача 2. Тема: «Интервальные оценки».
Задание:
При выборочном опросе 1200 телезрителей оказалось, что 456 из них регулярно смотрят программы телевидения НТВ. Постройте 99%-ый доверительный интервал, оценивающий долю всех телезрителей, предпочитающих программы телеканала НТВ.
Решение:
Для построения доверительного интервала для доли всех телезрителей, предпочитающих программы телеканала НТВ, можно воспользоваться методом Уилсона.
Метод Уилсона:
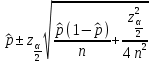
Где
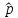выборочная доля, 
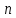- объем выборки, 
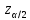- квантиль стандартного нормального распределения уровня 
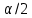.Подставим значения из условия задачи:
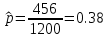
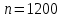
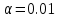
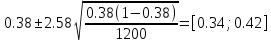
Таким образом, с вероятностью 99% можно утверждать, что доля всех телезрителей, предпочитающих программы телеканала НТВ находится в интервале от 34% до 42%.
Задача 3. Тема: «Проверка статистических гипотез»
Задание:
Крупный коммерческий банк заказал маркетинговое исследование по выявлению эффекта «премирования» (калькулятор, набор ручек и др.) как стимула для открытия счета в банке. Для проверки случайным образом было отобрано 200 «премированных» посетителей и 200 «непремированных». В результате выяснилось, что 79% посетителей, которым не предлагалась премия, и 89% посетителей, которым премия предлагалась, открыли счет в банке в течение 6 мес. Используя эти данные, проверьте гипотезу о том, что доля «премированных» посетителей, открывших счет в банке, существенно отличается от удельного веса «непремированных», открывших счет. Уровень значимости α = 0.05.
Решение:
Для проверки гипотезы о том, что доля «премированных» посетителей, открывших счет в банке, существенно отличается от удельного веса «непремированных», открывших счет, используется критерий хи-квадрат (χ²).
Пусть p1 - доля «непремированных» посетителей, открывших счет в банке, а p2 - доля «премированных» посетителей, открывших счет в банке. Тогда гипотезы будут следующими:
H0: p1 = p2
H1: p1 ≠ p2
Уровень значимости α = 0.05.
Рассчитаем значения χ² и найдем критическое значение χ²α(1) для уровня значимости α = 0.05 и степеней свободы df = 1 (так как имеем две выборки).
χ² = ((0.79 * 200 - 0.89 * 200)² / (0.79 * 200 + 0.89 * 200)) + ((0.21 * 200 - 0.11 * 200)² / (0.21 * 200 + 0.11 * 200)) = 10.24
Критическое значение χ²α(1) = 3.84.
Так как χ² > χ²α(1), то гипотеза H0 отвергается на уровне значимости α = 0.05 в пользу альтернативной гипотезы H1.
Таким образом, можно сделать вывод о том, что доля «премированных» посетителей, открывших счет в банке, существенно отличается от удельного веса «непремированных», открывших счет.
Задача 4. Тема: «Критерий согласия Пирсона»
Задание: С помощью критерия согласия Пирсона на уровне значимости α = 0,05
выяснить, можно ли считать случайную величину X, заданную в виде сгруппированного статистического ряда, нормально распределенной с параметрами
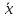и s, рассчитанными по выборке.| (xj; xj +1 ) | [1.2; 1.6) | [1.6; 2.0) | [2.0; 2.4) | [2.4; 2.8) | [2.8; 3.2) | [3.2; 3.6) |
| nj | 3 | 5 | 10 | 8 | 4 | 2 |
Рассчитаем значения
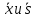:n = 32 (общее число наблюдений)
Выборочное среднее - xi равно
(1.4 * 3+ 1.8 * 5 + 2.2 * 10 + 2.6 * 8 + 3 * 4 + 3.4 * 2)/32 = 2.3375
Дисперсия равна
((1.4 - 2.3375)² * 3 + (1.8 - 2.3375)² *5 + (2.2 - 2.3375)² * 10 + (2.6 - 2.3375)² * 8 + (3 - 2.3375)² * 4 + (3.4 - 2.3375)² * 2) /32 ≈0.276
Стандартное отклонение равно
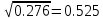
Рассчитаем наблюдаемое значение Кнабл статистики Пирсона по формуле:
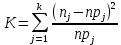
Эмпирические частоты nj уже известны, а для вычисления вероятностей pj, в предположении, что гипотеза справедлива, применим формулу
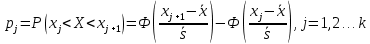
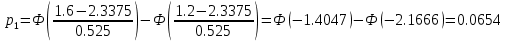
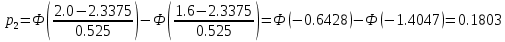
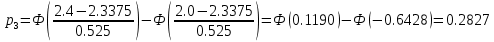
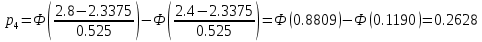
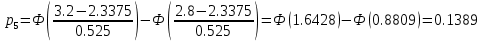
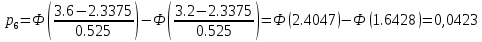
| (xj; xj1 ) | Выборочное среднее xi | Наблюдаемая частота nj | Вероятность pj попадания в j-й интервал | Ожидаемая частота npj | Слагаемые статистики Пирсона  |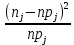
| [1.2; 1.6) | 1.4 | 3 | 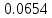 | 2,0928 | 0.39325 |
| [1.6; 2.0) | 1.8 | 5 | 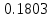 | 5,7696 | 0.10265 |
| [2.0; 2.4) | 2.2 | 10 | 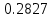 | 9,0464 | 0.10052 |
| [2.4; 2.8) | 2.6 | 8 | 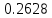 | 8,4096 | 0.01995 |
| [2.8; 3.2) | 3 | 4 | 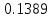 | 4,4448 | 0.04451 |
| [3.2; 3.6) | 3.4 | 2 | 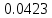 | 1,3536 | 0.30868 |
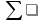 | | 32 | 1,2404 | 31,1168 | Кнабл=0.96956 |
Наблюдаемое значение статистики Пирсона равно Кнабл=0.96956
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то, чем больше ее наблюдаемое значение Кнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Ккр; +∞). Ее границу Ккр=
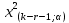находим по таблицам распределения «хи-квадрат» и заданным значениям α=0,05, число интервалов k=6, r=2 (так как параметры 
оценены по выборке): Ккр=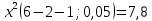 
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл< Ккр, поэтому есть основания не отвергать основную гипотезу.
Вывод: на уровне значимости 0,05 справедливо предположение о том, что данная случайная величина Х имеет нормальное распределение.
Задача 5. Тема: «Ранговая корреляция»
Задание: По заданной таблице рангов найти выборочный коэффициент ранговой корреляции Спирмена и проверить значимость полученного результата при α = 0.05.
Десять предприятий проранжированы по двум признакам: X — коэффициент механизации работ, Y — производительность труда.
| Ранг 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ранг 2 | 2 | 1 | 5 | 4 | 3 | 6 | 8 | 7 | 10 | 9 |
Решение:
Для нахождения выборочного коэффициента ранговой корреляции Спирмена (rS) по данной таблице рангов воспользуемся следующей формулой:
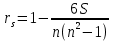,где d - разность рангов по соответствующим признакам для каждого предприятия, n - общее число предприятий.
Построим ранговую таблицу.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ri | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| si | 2 | 1 | 5 | 4 | 3 | 6 | 8 | 7 | 10 | 9 |
| ri- si | -1 | 1 | -2 | 0 | 2 | 0 | -1 | 1 | -1 | 1 |