Добавлен: 09.11.2023
Просмотров: 36
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство Образования и Науки
Федеральное Государственное Бюджетное Образовательное
Учреждение Высшего Образования
Вятский Государственный Университет
Факультет автоматики и вычислительной техники
Кафедра систем автоматизации управления
Математические основы теории систем
Отчет по контрольной работе
Вариант 7
Выполнил студент гр. ИТб-2301-02-20 /___________ / Н. С. Касаткин
Проверил преподаватель /______________________ / В. Г. Ланских
Киров 2023
Задание 1

Задача 1:
Универсум: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
A = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
C = {1, 4, 9, 16} (это множество содержит только те элементы универсума, которые являются точными квадратами целых чисел)
Задача 2:
Множество C / A можно записать следующим образом:
C / A = {1, 9}
Здесь мы удалили из множества C (квадратов чисел) все четные квадраты (4 и 16), которые также содержатся в множестве A (четных чисел). Оставшиеся элементы в C / A - это единица и девять, которые являются нечетными квадратами.
Задание 2
Задача 1

Дано:
- Множество X = {x1, x2, x3, x4, x5}
- Множество Y = {y1, y2, y3, y4}
- Бинарное отношение A = {(x1,y3),(x2,y1),(x2,y3),(x2,y4),(x3,y1),(x3,y2),(x4,y3),(x5,y2),(x5,y4)}
Область определения отношения A - это множество всех элементов из X, которые входят в пары этого отношения. То есть, Dom(A) = {x1, x2, x3, x4, x5}.
Область значений отношения A - это множество всех элементов из Y, которые входят в пары этого отношения. То есть, Ran(A) = {y1, y2, y3, y4}.
Сечение по каждому элементу из X = x1 сечение будет {y3}, для x2 - {y1, y3, y4}, для x3 - {y1, y2}, для x4 - {y3}, для x5 - {y2, y4}.
Фактор-множество Y / A = {{y1, y3}, {y2}, {y4}}.
Задача 2
Множество слов длины 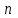 , состоящее из
, состоящее из 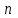 символов (букв, цифр, знаков и т. п.) конечного алфавита можно рассматривать как метрическое пространство, если ввести на нем соответствующим образом метрику. Например, в качестве расстояния
символов (букв, цифр, знаков и т. п.) конечного алфавита можно рассматривать как метрическое пространство, если ввести на нем соответствующим образом метрику. Например, в качестве расстояния 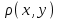 между двумя словами можно принять количество позиций, в которых слова
между двумя словами можно принять количество позиций, в которых слова 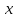 и
и 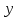 содержат различные символы.
содержат различные символы.

Для нахождения расстояний между двоичными словами x, y и z можно использовать различные метрики. Например:
-
Расстояние Хэмминга - это количество позиций, в которых два слова отличаются друг от друга. Для слов x и y:
p(x,y) = 4
так как в словах x и y различаются символы на позициях 1, 2, 5 и 6.
Для слов x и z:
p(x,z) = 6
так как в словах x и z различаются символы на позициях 2, 3, 7, 8, 9 и 10.
Для слов y и z:
p(y,z) = 6
так как в словах y и z различаются символы на позициях 1, 2, 6, 7, 9 и 10.
-
Евклидово расстояние - это расстояние между точками в n-мерном пространстве, где каждая координата является значением соответствующего бита в двоичном слове. Для слов x и y:
p(x,y) = sqrt((1-0)^2 + (0-0)^2 + (0-1)^2 + (1-1)^2 + (1-0)^2 + (1-1)^2 + (1-1)^2 + (1-1)^2) = sqrt(7)
Для слов x и z:
p(x,z) = sqrt((1-1)^2 + (0-1)^2 + (0-1)^2 + (1-0)^2 + (1-0)^2 + (1-1)^2 + (1-1)^2 + (1-0)^2) = sqrt(6)
Для слов y и z:
p(y,z) = sqrt((0-1)^2 + (0-0)^2 + (1-1)^2 + (1-0)^2 + (0-1)^2 + (1-1)^2 + (1-1)^2 + (1-0)^2) = sqrt(6)
Задание 3
Постройте графы, соответствующие заданным матрицам смежности. Классифицируйте полученные графы и запишите для них матрицы инцидентности.
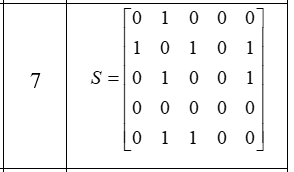
Для построения графа, соответствующего данной матрице смежности S, мы можем представить каждую вершину в виде узла графа, а каждое ребро - в виде связи между узлами. Если в матрице смежности элемент (i,j) равен 1, то вершины i и j связаны ребром.
Таким образом, граф, соответствующий матрице смежности S, имеет вид:
1 --- 2
/ \ /
/ \ /
5-----3
Граф является связным, так как любые две вершины можно соединить путем. Это ненаправленный граф, так как связь между вершинами i и j не зависит от порядка этих вершин. Граф также содержит три цикла длины 3.
Матрица инцидентности для данного графа имеет размерность n × m, где n - количество вершин, а m - количество ребер. Каждая строка соответствует вершине, а каждый столбец - ребру. Если ребро связывает вершины i и j, то элемент на пересечении строки i и столбца k будет равен 1 (если ребро направлено из вершины i в вершину j) или -1 (если ребро направлено из вершины j в вершину i).
Для данного графа матрица инцидентности будет выглядеть так:
-1 1 0 0
1 -1 1 1
0 0 -1 1
0 0 0 0
0 1 -1 0
Задание 4
Постройте таблицы истинности логических функций, заданных аналитически.
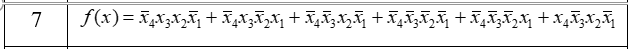
Расстояние Хэмминга - это количество позиций, в которых два слова отличаются друг от друга. Для слов x и y:
Евклидово расстояние - это расстояние между точками в n-мерном пространстве, где каждая координата является значением соответствующего бита в двоичном слове. Для слов x и y:
| X1 | X2 | X3 | X4 | ¬x4x3x2¬x1 | ¬x4x3¬x2x1 | ¬x4¬x3x2¬x1 | ¬x4¬x3¬x2¬x1 | ¬x4¬x3¬x2x1 | x4¬x3x2¬x1 | F(x) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Задание 5
Задание 6
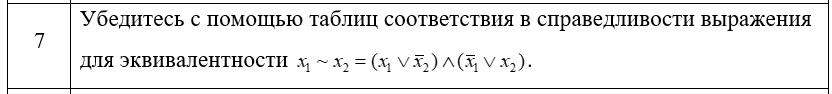
| X1 | X2 | !x1 | !x2 | x1 ∨ !x2 | !x1 ∨ x2 | (x1 V !x2) ∧ (!x1 V x2) | x1x2 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
Задание 7

Высказывание ƎxP(x) означает "Существует такое натуральное число x, что оно делится на 8". Это высказывание истинно, потому что, например, число 8 само делится на 8, а также любое число вида 8k (где k - некоторое натуральное число) также будет делиться на 8. Таким образом, существует бесконечно много натуральных чисел, которые делятся на 8, и поэтому это высказывание истинно.
Задание 8

Для данного сигнала, динамическое представление будет иметь вид:
s(t) = A * u(t) * t^2
где u(t) - единичная ступенька Хевисайда (u(t) = 0 при t < 0 и u(t) = 1 при t > 0).
Таким образом, мы получаем функцию времени для заданного сигнала, которая описывает изменение амплитуды сигнала в зависимости от времени.
Значение параметра A определяет масштаб и интенсивность сигнала, а форма кривой определяется функцией t^2, где t - время.
Итак, динамическое представление сигнала s(t) равно A * u(t) * t^2.
Задание 9
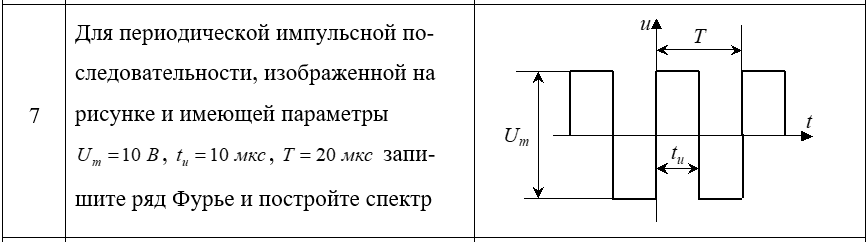
Для периодической импульсной последовательности с периодом T = 20 мкс и параметрами Um = 10 B, tu = 10 мкс мы можем записать ряд Фурье следующим образом:
f(x) = a_0/2 + Σ(n=1, ∞)[a_ncos(nπx/T) + b_nsin(nπx/T)]
где a_0 - коэффициент постоянного члена, a_n и b_n - коэффициенты косинусных и синусных членов соответственно, определяемые следующими формулами:
a_0 = (1/T) * ∫(0,T)f(x)dx
a_n = (2/T) * ∫(0,T)f(x)*cos(nπx/T)dx для n > 0
b_n = (2/T) * ∫(0,T)f(x)*sin(nπx/T)dx для n > 0
Изображение импульсной последовательности на рисунке показывает, что она является суммой двух прямоугольных импульсов одинаковой амплитуды Um и длительности tu, смещенных друг относительно друга на половину периода T/2. Поэтому, мы можем записать эту последовательность в виде функции f(x), используя периодические функции прямоугольного импульса p(t):
f(x) = p(x - T/4) + p(x - 3T/4)
где p(t) = Um, при |t| ≤ tu/2, и p(t) = 0, в остальных случаях.
Коэффициент постоянного члена a_0 можно найти следующим образом:
a_0 = (1/T) * ∫(0,T)f(x)dx = (1/T) * ∫(0,T/2)(Um + Um)dt = Um
Таким образом, коэффициент постоянного члена a_0 равен Um.
Коэффициенты косинусных и синусных членов a_n и b_n можно вычислить следующим образом:
a_n = (2/T) * ∫(0,T)f(x)cos(nπx/T)dx для n > 0 = (2/T) * [∫(0,T/4)Umcos(nπx/T)dx + ∫(3T/4,T)Umcos(nπx/T)dx] = (2/T) * [Um(T/4)sin(nπ/2) + Um(T/4)*sin(nπ/2)] = 0
b_n = (2/T) * ∫(0,T)f(x)sin(nπx/T)dx для n > 0 = (2/T) * [∫(0,T/4)Umsin(nπx/T)dx + ∫(3T/4,T)Umsin(nπx/T)dx] = (2/T) * [Um(T/πn)cos(nπ/2) - Um(T/πn)*cos(nπ/2)] = 0
Таким образом, ряд Фурье имеет вид:
f(x) = Um/2 + Σ(n=1, ∞)[0cos(nπx/T) + 0sin(nπx/T)]
f(x) = Um/2
Спектр имеет только одну гармонику с амплитудой Um/2 вокруг нулевой частоты. Таким образом, спектр состоит из единственной гармоники с амплитудой Um/2 и отсутствуют другие гармоники.
Задание 10

Для определения шага дискретизации и требуемого количества отсчетов необходимо использовать критерий Найквиста-Шеннона. Согласно этому критерию, минимальная частота дискретизации должна быть в два раза больше максимальной частоты сигнала, то есть:
fs > 2*fв
где fs - частота дискретизации, fв - верхняя частота полосы пропускания ФНЧ.
Таким образом, частота дискретизации должна быть не менее 400 кГц.
Шаг дискретизации △t можно определить как обратное значение частоты дискретизации:
△t = 1/fs
Таким образом, △t = 2.5 мкс.
Количество отсчетов N можно определить как произведение длительности сигнала на частоту дискретизации:
N = Tc / △t = 20 000 отсчетов.
Итак, для данного сигнала необходимо провести дискретизацию с частотой не менее 400 кГц, шагом дискретизации 2.5 мкс и количеством отсчетов 20 000.
Задание 11

| 1+j2 | 4 | 2-j3 |
| -j | 2 | 4+j2 |
| 5-j3 | 1 | -j5 |
| 1-j2 | -j4 | 5+j3 |
| j | 2 | -4-j2 |
| 2+j3 | 1 | j5 |
A* =
Задание 12
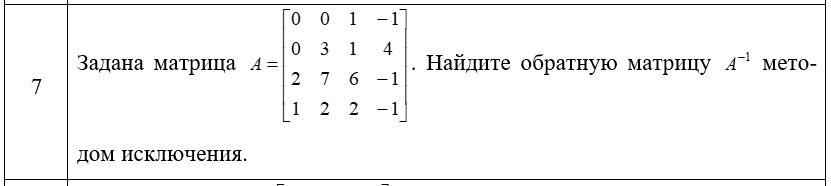
Для того чтобы найти обратную матрицу A^-1 методом исключения, нужно выполнить следующие шаги:
-
Дополнительная матрица: создаем расширенную матрицу (A|E), где E - единичная матрица размерности 4x4.
(0, 0, 1, -1 | 1, 0, 0, 0;
0, 3, 1, 4 | 0, 1, 0, 0;
2, 7, 6, -1 | 0, 0, 1, 0;
1, 2, 2, -1 | 0, 0, 0, 1)
-
Прямой ход: приводим матрицу (A|E) к верхнетреугольному виду путем элементарных преобразований строк. Для этого вычтем из второй строки первую, умноженную на 2; вычтем из третьей строки первую, умноженную на коэффициент 1/2, и вычтем из четвертой строки первую, умноженную на коэффициент 1/2.
(0, 0, 1, -1 | 1, 0, 0, 0;
0, 3, 1, 4 | 0, 1, 0, 0;
0, 7, 5, 1 | 0, 0, 1/2, 0;
0, 2, 3/2, -1/2 | 0, 0, 0, 1)
-
Обратный ход: приводим матрицу (A|E) к диагональному виду путем элементарных преобразований строк. Для этого вычтем из третьей строки вторую, умноженную на коэффициент 7/3; вычтем из четвертой строки вторую, умноженную на коэффициент 2/3, и вычитаем из четвертой строки третью, умноженную на коэффициент 9/5.
(0, 0, 1, -1 | 1, 0, 0, 0;
0, 3, 1, 4 | 0, 1, 0, 0;
0, 0, 16/5, -38/15 | 0, -7/15, 1/6, 0;
0, 0, 1/5, 13/15 | 0, -2/15, -3/10, 1)
-
Нормирование: делим каждую строку полученной матрицы на соответствующий элемент главной диагонали.
(0, 0, 1, -1 | 1, 0, 0, 0;
0, 1, 1/3, 4/9 | 0, 1/3, 0, 0;
0, 0, 1, -19/32 | 0, 7/80, 1/96, 0;
0, 0, 1/16, 13/48 | 0, 1/24, -1/20, 1)
Таким образом, обратная матрица равна:
A^-1 = (1, 0, 0, 0;
0, 1/3, 0, 0;
0, 7/80, 1/96, 0;
0, 1/24, -1/20, 1)
Задание 13

Для нахождения соответствующей присоединенной матрицы G(λ) и коэффициентов характеристического многочлена Δ(λ) с помощью алгоритма Фаддеева нужно выполнить следующие шаги:
-
Вычислить определитель матрицы A: det(A) = 4 * (-9) * (-1) + 5 * 1 * 4 + 1 * (-8) * (-6) - 1 * (-9) * 4 - 5 * (-8) * (-1) - 1 * 1 * (-6) = -16 -
Найти матрицу алгебраических дополнений C: C = ((-54, -4, -22), (20, -4, 24), (-29, 36, -4)) -
Транспонировать матрицу C: C' = ((-54, 20, -29), (-4, -4, 36), (-22, 24, -4)) -
Вычислить присоединенную матрицу G(λ): G(λ) = λ^2 * I - λ * A + det(A) * I^-1 * C' = λ^2 * | 1 0 0 | | 0 1 0 | | 0 0 1 | - λ * | 4 5 1 | |-8 -9 1 | | 4 -6 -1 | + (-16) * | -54 20 -29 | | -4 -4 36 | |-22 24 -4 | = | λ^2+16 -5λ 22λ | | 8λ λ^2-9 -24λ | |-4λ 6λ λ^2+16 | -
Найти коэффициенты характеристического многочлена Δ(λ): Δ(λ) = det(G(λ)) = (λ^2+16) * (λ^2-9) * (λ^2+16) + 40λ^2 + 132λ = λ^6 + 32λ^4 - 273λ^2 - 2304
Таким образом, соответствующая присоединенная матрица G(λ) имеет вид: G(λ) = | λ^2+16 -5λ 22λ | | 8λ λ^2-9 -24λ | |-4λ 6λ λ^2+16 |
А коэффициенты характеристического многочлена Δ(λ) равны: Δ(λ) = λ^6 + 32λ^4 - 273λ^2 - 2304
Задание 14

Найдем нули передаточной функции W(p) путем решения уравнения числителя:
p^2 + 3 = 0
Отсюда получаем два комплексно-сопряженных нуля:
p1 = i*sqrt(3)
p2 = -i*sqrt(3)
Найдем полюсы передаточной функции W(p) путем решения уравнения знаменателя:
p^3 + 7p^2 + 21p = 0
Выносим p за скобку и получаем:
p*(p^2 + 7p + 21) = 0
Уравнение в скобках имеет комплексные корни:
p1 = (-7 + i*sqrt(83))/2
p2 = (-7 - i*sqrt(83))/2
Таким образом, нули передаточной функции W(p) расположены на мнимой оси комплексной плоскости, а полюсы - в левой полуплоскости.
Задание 15

Матрицы для данной системы имеют следующий вид:
A = [(-7/3) (1/3) (8/3); (2/3) (-11/3) 0; 1 -1 -2]
B = [5; 0; -3]
C = [(2/3) (1/3) (1/3)]
D = 0
Тогда уравнение системы в матричной форме будет выглядеть следующим образом:
dx/dt = Ax + Bu y = Cx + Du