Файл: Контрольная работа по дисциплине Теоретическая механика (группа атпп20 бз) Фамилия, Имя, Отчество.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 55

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

АТПП-20 - ЗАОЧНОЕ

Контрольная работа по дисциплине «Теоретическая механика »

(группа АТПП-20- бз)



Фамилия, Имя, Отчество
Вариант №

Балтин Александр Васильевич
1

Батманов Лев Александрович
2

Букин Иван Сергеевич
3

Булычев Никита Петрович
4

Быков Роман Андреевич
5

Гайнутдинов Эмиль Мухетдинович
6

Головин Виталий Юрьевич
7

Жаков Алексей Александрович
8

Калабин Сергей Николаевич
9

Кочкин Никита Владимирович
10

Мельников Илья Витальевич
11

Потураев Антон Викторович
12

Уфимцев Александр Викторович
13

Хасанов Халиль Раифович
14


КРАТКАЯ ТЕОРИЯ
СИСТЕМА СХОДЯЩИХСЯ СИЛ

При решении задач статики аналитическим (численным) методом, используется метод, основанный на понятии о проекции силы на ось и на плоскость.

i - МАТЕМАТИЧЕСКАЯ СПРАВКА: Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление её совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону.

Проекцией силыFна ось Ox называется скалярная величина Fx, равная произведению её модуля F на косинус угла между силой и положительным направлением оси: 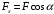(рисунок).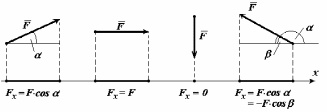



Рисунок - Проекция силы на ось: положительна, если угол α -острый;

равна нулю, если угол α - прямой (сила перпендикулярна оси); отрицательна, если угол α - тупой.
Проекцией силыFна плоскость Oxy называется вектор Fxy, заключенный между проекциями начала и конца силы F на эту плоскость.

В отличие от проекции силы на ось, проекция силы на плоскость является векторной величиной и характеризуется не только числовым значением, но и направлением в плоскости Oxy (рисунок).

По модулю 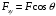, где θ - угол между векторами F и Fxy.

Проекция силы на плоскость используется, например, для нахождения проекций силы на оси, лежащие в этой плоскости (рисунок 22):

.


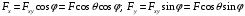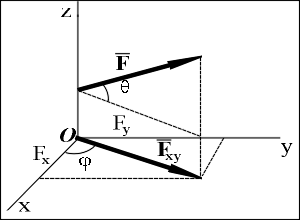
Рисунок - Проекция силыFна плоскость Oxy


ГЕОМЕТРИЧЕСКИЙ И АНАЛИТИЧЕСКИЙ СПОСОБЫ СЛОЖЕНИЯ СХОДЯЩИХСЯ СИЛ


Сходящимися называются силы, линии действия которых пересекаются в одной точке.



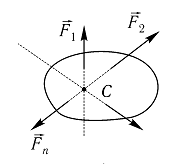
Система сходящихся сил имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия: .

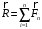Величину, равную геометрической сумме сил какой-нибудь системы, называют главным вектором этой системы сил. Если система сходящихся сил находится в равновесии, то её равнодействующая (а, значит, и главный вектор) должна равняться нулю.

Равнодействующая системы сходящихся сил - сила, оказывающая на твёрдое тело такое же механическое действие, как и данная система приложенных к телу сил.

Геометрическая сумма (главный вектор) любой системы сил определяется последовательным сложением сил системы по правилу параллелограмма или построением силового многоугольника.




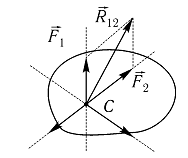
Аналитически по проекциям на оси координат:



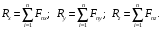
Модуль и направление равнодействующей определяется по формулам:



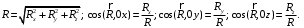
1. Сложение двух сходящихся сил. Треугольник и параллелограмм сил.

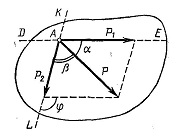
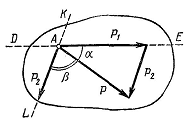
Если к телу приложены две силы, линии действия которых пересекаются в одной точке, то согласно аксиоме 4 (аксиома параллелограмма сил), их равнодействующая приложена в точке А пересечения линий действия сил изображается диагональю параллелограмма (рисунок), или построение параллелограмма сил можно заменить построение треугольника сил ABD (рисунок).



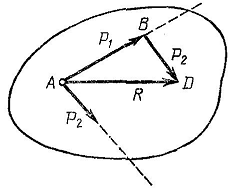
Направление равнодействующей силы 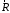по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.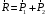



Используя формулы тригонометрии – теорему косинусов, можно определить модуль равнодействующей силы:



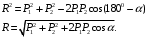
При помощи параллелограмма или треугольника сил можно решить обратную задачу, используя теорему синусов (рисунки).





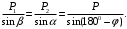
Так как 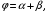то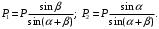

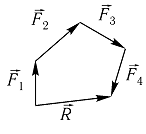
2. Многоугольник сил

Геометрически равнодействующая может быть найдена как замыкающая сторона силового многоугольника.

Данный способ является более простым и удобным. Пусть к твёрдому телу в точке А приложены сходящиеся силы F1, F2, F3,…Fn (рисунок, а). От произвольной точки О (рисунок, б) отложим вектор Оа, изображающий в масштабе силу F1, от точки а вектор аb, изображающий силу
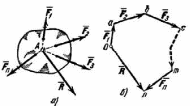
F2, от точки b вектор bc, изображающий силу F3 и т.д. Таким образом, соединяя начало первого вектора с концом последнего, получим вектор On=R, изображающий геометрическую сумму сил или главный вектор слагаемых сил:

.

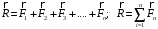Равнодействующая этих сил изображается замыкающей стороной многоугольника сил. От порядка, в котором откладываются вектора сил, модуль и направление R не зависит. Проделанное построение представляет собой результат последовательного применения правила силового треугольника.



Направление равнодействующей по контуру силового многоугольника противоположно направлению обхода этого контура, определяемому направлением первой силы.

Примечания.

1. Результат графического определения равнодействующей не изменится, если силы суммировать в другой последовательности, при этом получим другой силовой многоугольник - отличный от первого.

2. Фактически силовой многоугольник, составленный из векторов сил заданной системы, является ломаной линией, а не многоугольником в привычном смысле этого слова.

3. В общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
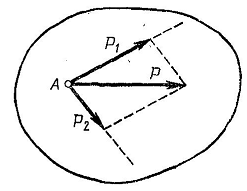
3. Сложение трёх сходящихся сил

Если к твёрдому телу приложены три сходящиеся силы (рисунок), не лежащие в одной плоскости, их равнодействующая приложена в точке пересечения линий действия сил и изображается диагональю параллелепипеда, построенного на этих силах.



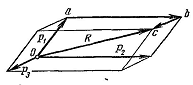
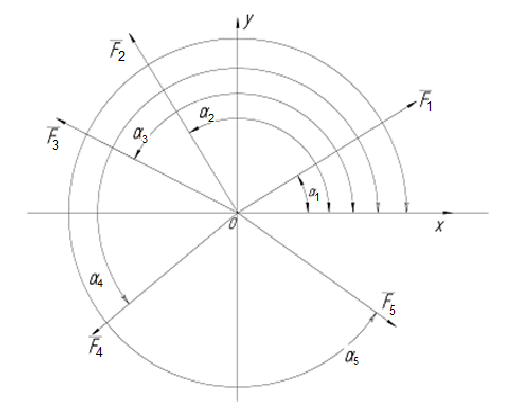
Диагональ параллелепипеда Oc является замыкающей стороной многоугольника Oabc:



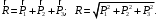
Правило сложение трёх сходящихся сил в пространстве называется правилом параллелепипеда сил.
Рекомендованный список литературы:

  1. Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — С. 9.

  2. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, в 10-ти томах. Том I — Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 169 с.

  3. Тарг. С.М. Краткий курс теоретической механики. 4-е изд. — М.: Наука, 1966. — С. 11.

  4. Игнатищев Р.М. Курс теоретической механики / Р.М. Игнатищев, П.Н. Громыко, С.Н. Хатетовский. - Мн.: УП «Технопринт», 2004. - 430 с.


КОНТРОЛЬНАЯ РАБОТА

«Определение равнодействующей системы сходящихся сил аналитическим и графическим методами»
Задание. Для заданной системы сходящихся сил (рисунок), определить равнодействующую силу по модулю и направлению, используя аналитический метод, и графические методы: метод построения силового многоугольника, метод параллелограмма сил.

Варианты выполнения задания взять из таблицы.

Алгоритм решения:

  1. Составить расчётную схему, согласно своему варианту.

  2. Составить анализ решения и записать формулы для данного решения.

  3. Решить задачу аналитическим способом: найти проекцию равнодействующей силы на оси X и Y; определить модуль и направление равнодействующей силы; построить равнодействующую в координатной плоскости 0xy.

  4. Решить задачу геометрическим способом – метод построения силового многоугольника.

  5. Сделать вывод о полученных результатах аналитическим и геометрическим способами.




№

F1, Н
F2, Н
F3, Н
F4, Н
F5, Н
α1, град
α2, град
α3, град
α4, град
α5, град



1
1
2
3
4
5
150
60
180
270
0



2
1
2
3
4
5
180
90
30
240
330



3
1
2
3
4
5
120
30
225
45
0



4
1
2
3
4
5
330
135
45
210
300



5
1
2
3
4
5
315
150
60
180
270



6
1
2
3
4
5
300
180
90
45
240



7
1
2
3
4
5
90
0
240
330
135



8
1
2
3
4
5
45
310
300
180
90



9
1
2
3
4
5
45
120
330
180
210



10
1
2
3
4
5
60
180
270
0
120



11
1
2
3
4
5
180
270
0
120
30






12
12
8
6
4
10
30
45
0
60
300




13
8
12
2
10
6
0
45
75
30
270




14
20
5
10
15
10
0
60
75
150
210




15
3
6
12
15
9
15
45
45
120
270




16
6
12
15
3
18
0
15
60
150
300




17
18
4
6
9
8
20
45
0
60
300




18
9
10
4
18
12
30
45
0
30
270




19
10
15
10
10
5
0
60
60
150
210




20
6
15
6
6
6
0
45
45
120
270




21
10
5
8
10
12
15
15
75
150
300

Смотрите также файлы