ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2021
Просмотров: 885
Скачиваний: 4

/ '( * ) =
2х
V(2
jc
2 + 0 .3 )3
, / '( * ) =
8х -0 .6
л](2х2
+0.3)5
max I
[0.7;1.3]
/ " w | *
8-1.3 -
0.6
д/ (2 • 0.7
2
+0.3
)5
6.98.
Положим
М 2 = 7 ,
тогда
неравенство
(*)
примет
вид
0.6
3
-7
12
«^
< 0.0005, откуда
п >
252, т.е.
п
>
16;
возьмем « = 20 .
Вычисление интеграла проводим по формуле
У0 +У20
где
h = -
—- = — = 0.003;
п
20
j c , =
0.7
+
ih
( / =
0,1,2,..,19).
+ 0.3
i
x i
У(
0
0.7
0.88386
1
0.73
0.85572
2
0.76
0.82898
3
0.79
0.80366
4
0.82
0.77973
5
0.85
0.75700
6
0.88
0.73546
7
0.91
0.71501
8
,
0.94
0.69551
9
0.97
0.67700
10
1.00
0.65937
11
1.03
0.64259
■
12
1.06
0.62657
48
I
h
=
I
где
13
1.09
0.61140
14
1.12
0.59669
15
1.15
0.58272
16
1.18
0.56935
17
1.21
0.55658
18
1.24
0.54431
19
1.27
0.53253
20
1.30
0.52129
Таким образом,
0.88386 + 0.52129
*0.03
2
3)
Согласно
b - a
1
.
6
-
1.2
+ 12.77022
1
=
0
.
40418 * 0 .4 0 4 .
условию
п =
8
.
поэтому
= 0.05.
п
8
Расчетная формула имеет вид
h
* ^ (.У
0
+
4
Л +
2У1
+
4
УЗ
+
2У4
+ 4^5 +
2У6 + *У1 + 2У8
)»
y i ^ y ( x i ) = Sm(2Xi~ 2 A ) , X i = 1.2+ ih
(| =
0
,
1
,
2
,...,
8
).
x f
+1
Вычисления значения функции запишем в таблице:
i
Xi
У1
0
1.2
0.1211
1
1.25
0.1520
2
1.30
0.1782
3
1.35
0.2000
4
1.40
0.2176
5
1.45“
0.2312
;
6
1.50
0.2410
7
1.55
0.2473
8
1.60
0.02503
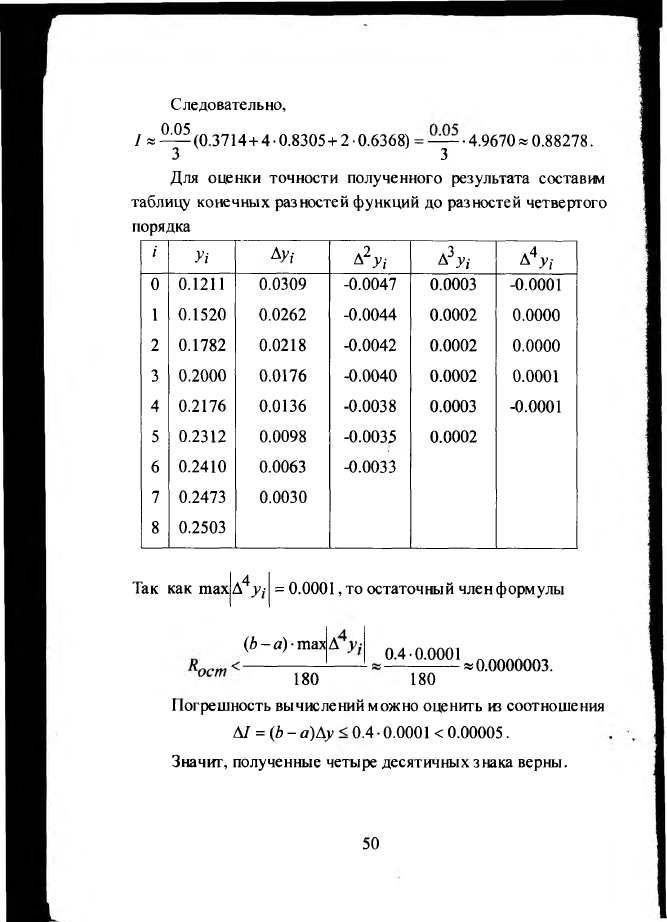
Следовательно,
/ я ^ ^ ( 0 .3 7 1 4 + 4-0.8305+2 • 0.6368) = — • 4.9670 * 0.88278.
3
3
Для оценки точности полученного результата составим
таблицу конечных разностей функций до разностей четвертого
порядка
/'
У1
Ду,-
А
2У1
Д
ЪУ1
Д
4y j
0
0.1211
0.0309
-0.0047
0.0003
-
0.0001
1
0.1520
0.0262
-0.0044
0.0002
0.0000
2
0.1782
0.0218
-0.0042
0.0002
0.0000
3
0.2000
0.0176
-0.0040
0.0002
0.0001
4
0.2176
0.0136
-0.0038
0.0003
-
0.0001
5
0.2312
0.0098
-0.0035
0.0002
6
0.2410
0.0063
-0.0033
7
0.2473
0.0030
8
0.2503
Так как шах Л4Л =
0
.
0001
, то остаточный член формулы
( Ъ-а) -
max Д
0.4 0.0001
«0.0000003.
180
180
Погрешность вычислений можно оценить ю соотношения
А/ =
(Ь
-
а)
Ду < 0.4 • 0.0001 < 0.00005.
Значит, полученные четыре десятичных знака верны.
50
Лабораторная работа №13
ЧИ СЛЕН Н О Е РЕШ ЕНИЕ ОБЫ КН О ВЕН НЫ Х
ДИ Ф Ф ЕРЕН ЦИ А ЛЬН Ы Х УРАВНЕНИЙ.
ЗАДАЧА КОШ И
Задание.
Получить с точностью 10- ^ численное решение
дифференциального уравнения , удовлетворяющее
заданному начальному условию методом Эйлера и
классическим
методом
Рунге-Кутты
четвертого
порядка. Используя метод Эйлера, найги решение
обыкновенного
дифференциального
уравнения
у ' = f ( x , у
) , удовлетворяющего начальным условиям
,К*о) =
УО т
отрезке
[a,b
] ; шаг
И =
0.1.
? 2
№1.
у ’ + - % - ? - =
0, Я 0 ) = 1» * е [0 ,5 ].
х
+1
№
2
.
у ' = - у х + х, у(0) = 2,
х е[0,5].
№3. 2
у'у
=
{у2 -
l)x,
y(l)
= 2, * е [l,3].
№4. у ' = — + х 2 cosx, у(я)= 1 , х е
х
№5. (l +
е х
)у' = — , у(о) = 1,
х
е [0,2].
У
№ 6.
у'х = у
+
х 2
,
y ( l) = 1,
jc
е [l,4 ].
№7.
у ' = (у
+ 1
) 2
lnjc, y(l) = l, jce[l,2].
№
8
.
у ' = ytgx
+ cos
2
jc, y(
0
) =
1
, jc e [o,l].
№9.
y '= y ^X
y(l) = e, x
e
[l,5].
JC
51

№
10
.
у ' + ^ = х 2 ,
Я
0
= 1>
х е
[l’3] •
х
№11. / =
Я 0 = °» *е[1,3].
л:
№
12
.
у ’ = х + ^ ,
Я 1) = 1» * е [
1
,
2
].
л:
№13.
у ' = ух,
Я 0 = 1» *е[1,2].
2
№14. / =
Я 0 = 1, х е [1,2.5].
х
№ 15.
у A
Z Z i l H , y(l) =
0
, х е [
1
,
6
].
л:
№16. / = £ ± f , Я 0 = о »
х
е [
1
,з] •
х
№17.
у ' + 2ух = хе~ х
, Я 0 ) = 0> дсе[0,4].
♦
л
№18.
у '
+
у
cos* = S11^ * , Я
0
) =
0
, * е [
0
,
2
].
№19.
y ' + y t g x -
sin2x = 0, >>(о) = — 1, х е [0 ,2 ].
№
20
.
у ' - —
+ — ,
у(е) = 0,
х е [ е ,е
21
.
jc
In JC
Образец выполнения задания
Метод Эйлера
•У = —
,
у(0) = \,
"[
0
,
1
].
у + х
Д
ля
решения используем формулу Эйлера
У1
+1
= У { + Ь - Д х {, у{),
(/ = 0,1,2,....).
52