ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2021
Просмотров: 888
Скачиваний: 4
№8.
№9.
№ 10.
№
11
.
№
12
.
№13.
№14.
№15.
№ 16.
1)2 - 1 =
о
,
( х > 0 )
л
/х
+ 1 -
у
= 0;
\ х 2 + у 2 - 2 х = 0,
( у > 0 )
[ln(x)
- у =
0
;
Ixcos(x)
- у
=
0
,
\ 7
7
( х <
0
).
1
х
2 + / - 1
=
0
;
2 х 2 + у 2 - Ы 0 ,
* 2 / 3 + г = 0;
fsin(x)->> = О,
7
9
(х <
0
).
|х-
+ у - 1 = 0;
х 2 + у 2 - 2 у = 0,
( х
>
0
).
е~х - у = 0;
( , +
1
)
2
+ ( ^
1
)
2
- . =
0
,
л/х +
1
— jv —
1
=
0
;
^ + ^ /
7
-
1
=
0
,
х
2
+
^ 2
-
2
х =
0
;
О > >
0
).
);
1
x sin (x )-> ' =
0
,
,
7
(х >
0
).
х +>>
- 1
=
0
;
36
№17.
\ х 2 + у 2 - 2 у = 0,
[ln(x +
1
) -
2у
=
0
;
( х > 0 ) .
№18.
№19.
х 2 + у 2
- 1
=
0
,
2хе~х - у =
0
;
fx s in (x ) -y -
0
,
[х
2
+ у
2
-
1
=
0
;
( х
>
0
).
(х <
0
).
№20.
Ь 2 + Ь 2 -
i = o ,
х 2 + у 2 - 2 х =
0
;
( у <
0
).
Образец выполненш задания
Метод итерации
Дана система нелинейных уравнений
lsin(x -
0
.
6
) -
у
=
1
.
6
,
(Зх - cosy - 0.9.
Перепишем данную систему в виде
у -
s i n ( x -
0
.
6
) -
1
.
6
,
1
х - - c o s y + 0.3.
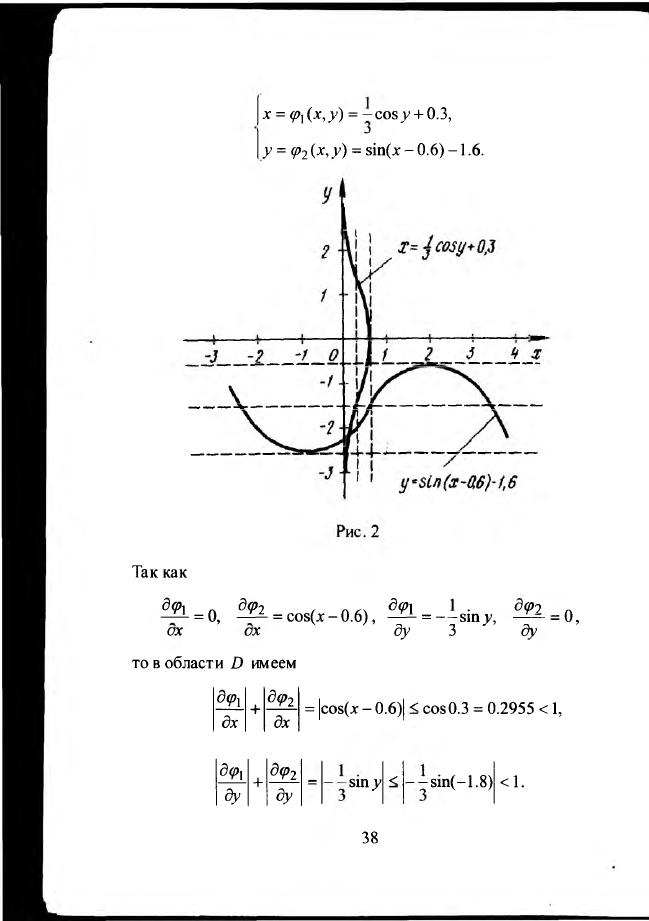
Отделение корней производим графически (рис. 2). Из графика
видим, что система имеет одно решение,, заключенное в
области
D :
0 < х < 0.3; - 2 .2 с у < -1 .8 .
Убедимся в том, что метод итераций применим для
уточнения решений системы, для чего запишем ее в
следующем виде:
37
х = <рх
(х,у) = - c o s y + 0.3,
y = q>
2
(х,
у
) = sin(x -
0
.
6
) -
1
.
6
.
Так как
дф\
л
дф2
,
л , ч
д(р\
1 .
дер?
п
— !- =
0
, —
= c o s ( x -
0
.
6
) , —— = - - s i n y , —— =
0
,
ох
ох
ду
3
ду
то в области
D
имеем
д<р\
+
д(р2
дх
дх
д(Р\
н-
д<р2
ду
ду
= |cos(x - 0.6)| < cos0.3 = 0.2955 < 1,
sin у < — — sin(—
1
.
8
)
<
1
.
38

Таким образом, условия сходимости выполняются.
Вычисления производим по формулам
1
*и+1 = - c o s
у„
+0.3,
3
у
п+1
= sin(x„ -
0
.
6
) -
1
.
6
.
За начальное приближение принимаем
xq
=0.15;
уо = - 2 .
Вычисления располагаем в таблице:_______________
п
х п
Уп
0
0.15
-2
1
0.1616
-2.035
2
0.1508
-2.0245
3
0.1539
-2.0342
4
0.1510
-2.0313
5
0.1519
-2.0341
6
0.1510
-2.0333
7
0.1513
-2.0341
8
0.1510
-2.0340
Ответ:
х
« 0.151;
у
* -2.034.
Метод Ньютона
Дана система нелинейных уравнений
fsin(2x -
у)
- 1
,2х
= 0.4,
[0.8х
2
+1.5у
2
=1.
Отделение корней произведем графически (рис.З).
Из рисунка видно, что значения для л: можно брать
исходя
ю следующих условий: из
первого уравнения
-1 < 1.2jc + 0.4 < 1, т. е. -1 .1 6 <
х <
0.5; из второго уравнения
- л /1.25 <
у <
л/1.25 , т.е.
—1.12 <дг <1.12. Таким образом,
-1.12 < jc < 0.5.
39

Рис. 3
Система имеет два решения. Уточним одно из них,
принадлежащее области
D
: 0.4 <
х
< 0 .5
;
- 0.76 <
у
<
-0 .7 3 . За
начальное приближение примем
jcq
=0.4;
у $
= -0 .7 5 .
Имеем,
[
F\
(jc ,
у )
=
sin(2jc
-
у ) -
1
.2 х -
0.4,
[F
2
(x,y) = 0.8jc
2
+1.5y
2
- l .
= 2 c o s ( 2 j c -
у )
- 1 . 2 ,
дх
dF,
дх
— =
\ .6х.
- - cos(
2
x -
у),
ду
dF,
ду
= Ъу.
Уточнение корней проводим методом Ньютона
{
■*72 + 1
= Х П
+
Уп
+1
~ Уп
Щ ( хюУп )
Щ (хп>Уп)
д /г
где
Ип =
— ^
кп -
^к„
Ап -
•
дх
ду
dF2(x„ ,y
,,)
dF2(xn ,y n )
дх
ду
40