Задача 1. Сигналы и их спектры.

1. 
   Гармоническое колебание
   

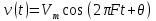
Сигнал описывается формулой:Постройте временные диаграммы, амплитудный и фазовый спектр для двух значений частоты F₁ и F₂.Исходные данные представлены в таблице 1:

τ, мсек	А	F, кГц	Vm, В	θ, град	Т, мсек
1,8	7,6	52	9,5	60	17

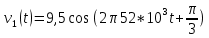
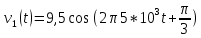
Решение:Временная диаграмма сигнала v₁(t) с частотой F₁=52 кГц представлена на рисунке 1.1: Временная диаграмма сигнала v₂(t) с частотой F₂=5 кГц представлена на рисунке 1.2: Спектральную плотность сигнала можно получить применением прямого преобразования Фурье. Для точной аппроксимации его рядом Фурье достаточно иметь только один член ряда, поскольку сигнал совпадает с одной из базисных функций разложения по Фурье, которая совпадает по частоте с f= F₁ и имеет начальную фазу θ, т.е. его спектр состоит всего из одной составляющей с частотой F₁=52 кГц, амплитудой V_m=9,5 Ви начальной фазой θ=60 град. Амплитудный спектр сигналов v₁(t) и v₂(t) представлен на рисунке 1.3, фазовый спектр-на рисунке 1.4.

2. 
   Импульсный сигнал.
   

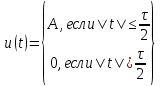
Рассчитать спектральную плотность импульса, определенного следующим образом:Построить графики амплитудного и фазового спектра.Определить ширину спектра, как зависит ширина спектра от длительности импульса.Найти произведение длительности импульса на ширину его спектра.Исходные данные представлены в таблице 1.Решение:

---

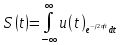
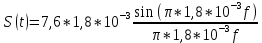
Спектральная плотность импульса определяется путем преобразования Фурье:Для прямоугольного импульса при интегрировании на интервале его существования спектральная плотность описывается выражением:Так как функция спектральной плотности является действительное число, то фазовый спектр принимает одно из двух значения 0 или π радиан.Значение спектральной плотности при нулевой частоте равно площади импульса Аτ.Амплитудный спектр-модуль спектральной плотности, график представлен на рисунке 1.5, фазовый спектр на рисунке 1.6.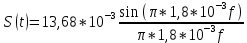Во многих практических приложениях определяют ширину спектра видеоимпульсов как полосу частот в пределах одного (первого) лепестка, в связи с существенным уменьшением S(f) в последующих лепестках. 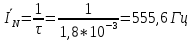Учитывая, что ширина спектра определяется лишь для реально существующих частот, ширина спектра для данного случая равна:Ширина спектра импульса обратно пропорциональна длительности импульса. 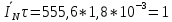Произведение ширины спектра импульса на его длительность – величина постоянная:Рассчитанное значение соответствует ожидаемому.

3. 
   Периодическая последовательность прямоугольных импульсов.
   
4. 
   Сигнал образован периодическим повторением импульса, заданного в п 1.2 и описываемого выражением:
   

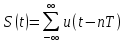
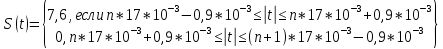
Рассчитать и построить временные диаграммы и графики амплитудного и фазового спектров сигнала. Построить векторные диаграммы первых трех гармонических составляющих сигнала, а так же суммы этих гармоник.Исходные данные представлены в таблице 1.Решение:Огибающая амплитуд спектральных составляющих линейчатого спектра для периодической последовательности прямоугольных импульсов определяется синковой функцией:

---

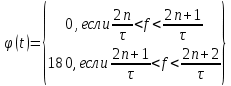
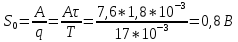
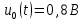
,где частота f принимает только дискретные значения f=nF₁, n=1,2,3…, которые являются гармониками частоты следования импульсов F₁=1/Т.Значение огибающей при f=0 S_max=2A/q= В. Амплитудный мпектр представлен на рисунке 1.8.Фазовый спектр сигнала представлен на рисунке 1.9:Постоянная составляющая сигнала: Амплитуды гармонических составляющих последовательности импульсов можно определить по формуле:

---

Смотрите также файлы

• Анализ методической работы за 20222023 учебный год.docx

• Инструкция подачи заявления на временное трудоустройство через портал Работа России.pdf

• Статистика аварий, катастроф, пожаров Выпонил Курсант учебной группы 7120 Болатов Нурзат.pptx

• Отчет по производственной практике (вид практики).docx

• Практическое задание 1,2,3.docx