ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 9
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Порядок выполнения контрольной работы:
1.1 Для проверки наличия грубых погрешностей используем критерий Граббса по ГОСТ Р 8.736.
Рассчитаем оценку измеряемой величины N*, по формуле:
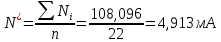
где Ni – i-й результат измерений, мА;
n – число результатов измерений, штук.
Затем рассчитаем среднее квадратическое отклонение (СКО) S(N*), мА, ряда результатов измерений:
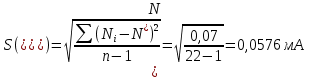
После этого рассчитаем значения критерия Граббса h1 и h2, соответствующие наименьшему Nmin и наибольшему Nmax результатам измерений из выборки:
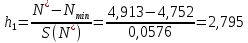
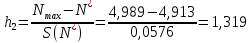
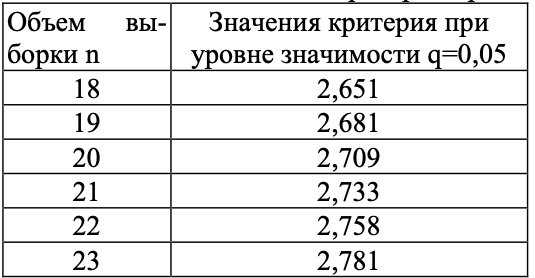
Сравниваем h1 и h2 с теоретическим значением hт критерием Граббса, при уровне значимости q=0,05, n=22, hт=2,758, по таб.1.1.
Так как,
h1 > hт, то Nmin исключаем, как маловероятное значение.
h2 hт, то Nmax сохраняем в ряду измерений.
Вновь вычисляем среднее арифметическое и СКО уменьшенного по объему ряда результатов измерений и повторяет процедуру проверки наличия грубых погрешностей.
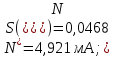
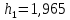
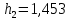
Сравниваем h1 и h2 с теоретическим значением hт критерием Граббса, при уровне значимости q=0,05, n=21, hт=2,733.
Таблица 1.1 – Значение критерий Граббса
h1 hт, то Nmin сохраняем в ряду измерений.
h2 hт, то Nmax сохраняем в ряду измерений.
1.2 Для проверки гипотезы о нормальном распределении результатов измерений используем составной критерий, приведенный в ГОСТ Р 8.736.
Критерий называется составным, потому что состоит из двух критериев, которые проверяются последовательно.
Критерий 1 формулируется следующим образом:
- гипотеза о нормальности по критерию 1 не отвергается, если выполняется неравенство
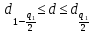
по таблице
г
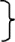де q1 – уровень значимости критерия 1; 
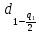– квантиль по значению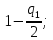 
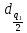– квантиль по значению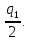 
Примем уровень значимости критерия 1 равным q1=0,02.
Таблица 1.2 – Значение квантилей
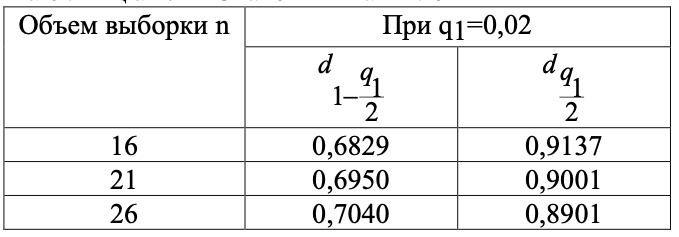
В нашем случае, при n=21,
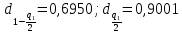
Вычисляем смещенную оценку СКО – по формуле:
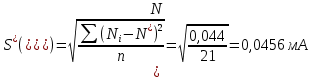
Затем вычисляем параметр "d" по формуле:
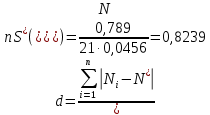
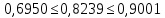, гипотеза о нормальности по критерию 1 не отвергается.Критерии 2 формируется следующим образом,
- гипотеза по критерию 2 не отвергается, если число разностей Ni-N*, превышающих по размеру произведение
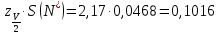,т.е
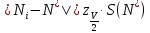, окажется не более «m» раз .Здесь
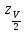– квантиль распределения нормированной функции Лапласа, соответствующая вероятности V/2. Примем уровень значимости критерия 2 равным q2=0,02.
Таблица 1.3 – Значение параметров
По таблице 1.3 определяем значения: m=2, V=0,97.
Таблица 1.4 – Значение
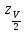
По другой таб.1.4 определяем
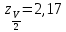
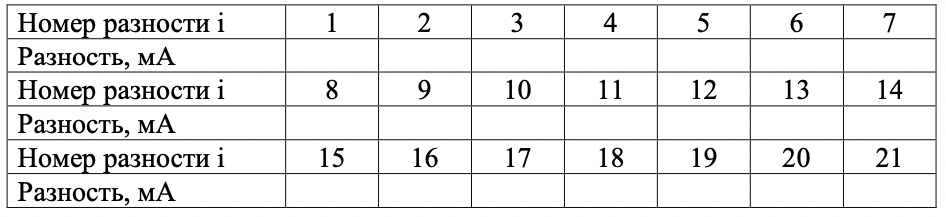
Абсолютные значения разностей Ni-N*| приведены в таблице 1.5.
Таблица 1.5 – Абсолютные значения разностей Ni-N*|
| Номер размерности i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Размерность, мА | 0,008 | 0,002 | 0,023 | 0,011 | 0,035 | 0,049 | 0,068 |
| Номер размерности i | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Размерность, мА | 0,022 | 0,029 | 0,081 | 0,076 | 0,048 | 0,046 | 0,015 |
| Номер размерности i | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Размерность, мА | 0,023 | 0,05 | 0,015 | 0,084 | 0,013 | 0,076 | 0,015 |
По критерию 2 гипотеза о нормальном распределении результатов измерения принимается, т.к абсолютные значения разностей не превышают по размеру 0,1016.
Вывод: по критериям 1 и 2, распределение результатов измерений ряда соответствует нормальному распределению.
1.3 Для представления статистического ряда в виде таблицы необходимо сгруппировать результаты измерений в j интервалах. При j=7 длина одного интервала L, мА, составит
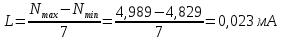
Затем формируем таблицу 1.6.
Таблица 1.6 – Статистический ряд результатов измерений
| Параметры | Значения параметров для интервала | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Границы интервалов, мА | 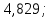 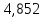 | 4,852; 4,875 | 4,875; 4,898 | 4,898; 4,921 | 4,921; 4,944 | 4,944; 4,967 | 4,967; 4,989 |
| Кол-во результатов измерений в интервале mj, шт | 2 | 1 | 4 | 2 | 6 | 3 | 3 |
| Частота для интервала Pj(N*) | 0,0952 | 0,0476 | 0,1905 | 0,0952 | 0,2857 | 0,1429 | 0,1429 |
| Статистическая плотность вероятности для интервала fj*(N*), мА-1 | 4,1408 | 2,0704 | 8,2816 | 4,1408 | 12,4224 | 6,2112 | 6,2112 |
Частоту для интервалов, находим по формуле:
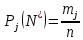
для интервала:
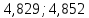
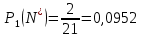
Аналогично для интервалов 2-7.
Значение статистической плотности вероятности fj*(N*), рассчитываемые по формуле:
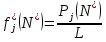
для интервала:
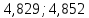
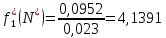
Аналогично для интервалов 2-7.
1.4 Для построения гистограммы на каждом интервале, обозначенном дополнительными делительными штрихами на горизонтальной оси построим прямоугольник с высотой, равной соответствующему этому интервалу значению плотности вероятности. При этом стороны прямоугольников, как правило, не будут совпадать с координатной сеткой графика, рис.1.1.
1.5 Для сглаживания статистического ряда нужно использовали теоретическую плавную кривую плотности нормального распределения, точки для построения которой получили по формуле
Полученные результаты позволяют получить расчетную величину параметров хи-квадрата:
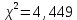
Для совпадения фактического закона распределения с теоретическим законом нормального распределения необходимо, чтобы выполнялось следующее условие:
2 ≤ 2q
где 2q – теоретическое граничное значение параметра хи-квадрат, которое определяется по таблице.
Для получения табличного значения необходимо определиться с двумя параметрами:
- уровнем значимости q, который показывает вероятность того, что законы не совпадут.
Примем, q = 0,02;
- числом степеней свободы, которое определяется в зависимости от числа интервалов n и числа определяемых по статистике параметров, необходимых для совмещения модели и гистограммы r.
Для нормального закона распределения r = 2, так как закон однозначно характеризуется двумя параметрами – СКО и МО (математическим ожиданием).
Число степеней свободы определяется по формуле:
=n–1–r=7–1–2=4
Таким образом, табличное значение
.
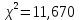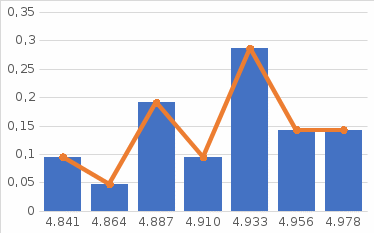
Рисунок 1 - Гистограмма и теоретическая кривая распределения
4.8 Рассчитаем доверительные границы случайной погрешности , мА:
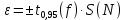
где t0,95(f) - коэффициент Стьюдента для доверительной вероятности Р = 0,95 и числа степеней свободы f=20, t0,95(f) = 2,086.
S(N) – СКО среднего арифметического оценки измеряемой величины, мА.
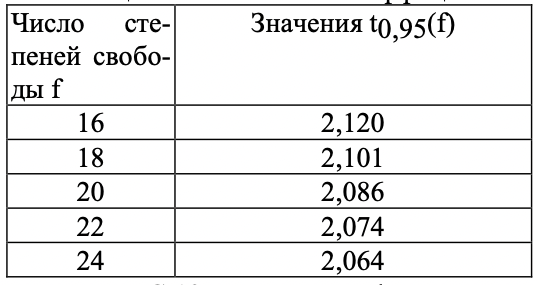
Значение коэффициента Стьюдента взяли из таблицы 1.7 по числу степеней свободы f=n-1.
Таблица 1.7 – Критерий Стьюдента
Рассчитаем СКО среднего арифметического оценки измеряемой величины по формуле:
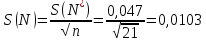
Таким образом,
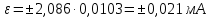
Расчет доверительных границ неисключенной систематической погрешности (НСП) (Р), мА, следует провести по формуле
где ЦП – НСП цифровой части прибора ИРТ 1730У;
АД – НСП адаптера, встроенного в прибор ИРТ 1730У;
КАБ – НСП кабельных соединений в ИК ИИС.
Приняли следующие предельные значения НСП: ЦП=0,01 мА; АД=0,005 мА; КАБ=0,01 мА.
Тогда,
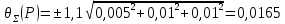
Определение доверительных границ погрешности оценки измеряемой величины , мА:
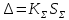
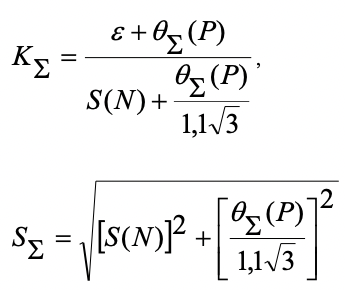
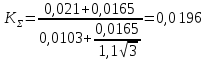
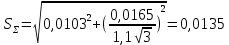
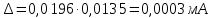
Результат измерения тока: 4,92100,0003 мА; Р0,95.