Симплекс-таблица заполняется в следующей последовательности: столбец i, строка С, столбец Бx, столбец Сб, столбец A0, столбцы A1,…,An. Так заполняются первые m строк.

В нулевой столбец (m+1)-й строки записывается значение линейной формы для имеющегося опорного плана. Это значение вычисляется по формуле
. (9)
В последующие клетки (m+1)-й строки записываются значения оценок векторов условий Aj (величины j), которые вычисляются по формуле

(10)

Базисные разности si=0.

Для проверки опорного плана на оптимальность просматриваем (m+1)-ю строку. При этом могут встретиться такие случаи:

1) Все разности j0. Тогда опорный план X0 является оптимальным и minZ=Z0.

2) Для некоторого фиксированного j j>0 и все коэффициенты xij0, . Тогда линейная форма не ограничена множеством допустимых решений задачи. В обоих случаях процесс вычисления на этом заканчивается.

3) Для некоторых индексов j имеются j>0 и для каждого такого j, по крайней мере, одно из чисел xij>0. Это свидетельствует о том, что опорный план не является оптимальным и его можно улучшить за счет введения в базис вектора, отвечающего одной из таких разностей. В базис необходимо ввести тот вектор, которому отвечает maxj. Если таких разностей несколько, то берут вектор с меньшим номером.

Пусть . Тогда в базис следует ввести вектор Ak на место вектора, которому отвечает минимальное значение выражения
. (11)
Необходимо вывести из базиса вектор Asr, новый базис будет состоять из векторов: As1,As2,…,Asr-1,Asr+1,…,Asm,Ak. В этом случае xrk называют разрешающим элементом симплексной таблицы. Столбец k и строка r называются разрешающими.

Все элементы новой симплексной таблицы с нулевого столбца по n-й и с первой строки по (m+1)-ю преобразовываются при переходе к новому опорному плану по следующим рекуррентным формулам:

---

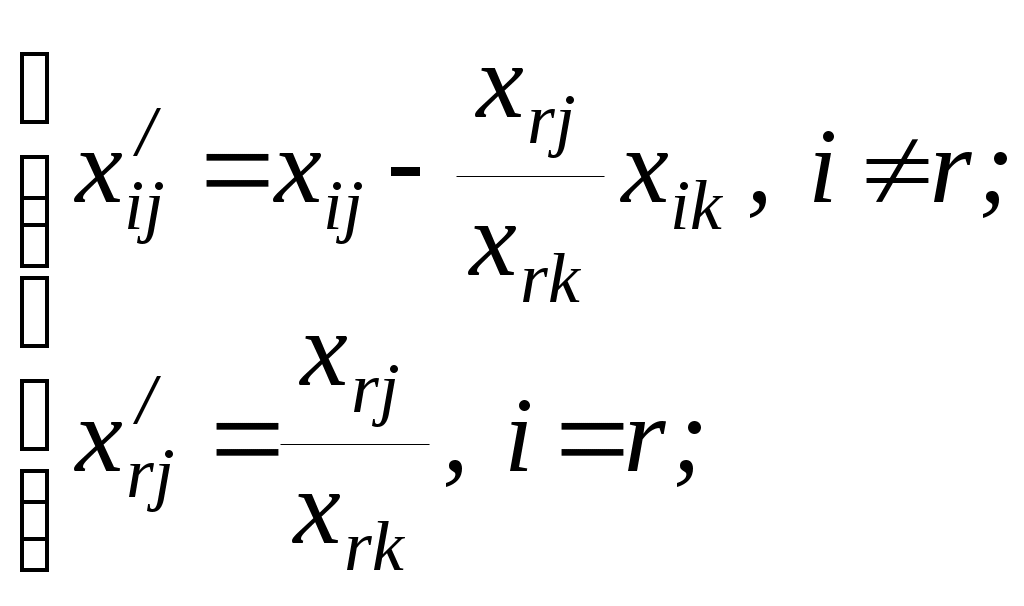
(12)


Обычно симплексную таблицу преобразовывают следующим образом. Направляющую строку r делят на разрешающий элемент xrk. В новой симплексной таблице на месте разрешающего элемента получается единица: x =1, а на месте разрешающего столбца получается единичный вектор с единицей в направляющей строке. Остальные строки преобразовываются так: из той строки исходной таблицы, которую необходимо преобразовать, вычитаем преобразованную направляющую, умноженную на тот элемент строки, на месте которого следует получить нуль.

В результате преобразования нулевой симплекс-таблицы по формулам (12) получаем следующую таблицу, в которой содержится новый опорный план. Опять просматриваем (m+1)-ю строку. Если все j0, то опорный план оптимален. В противном случае переходим к новому опорному плану. Процесс продолжается до тех пор, пока придем либо к оптимальному плану, либо убедимся в неограниченности линейной формы. Алгоритм симплексного метода в виде блок-схемы представлен на Рисунке 1.


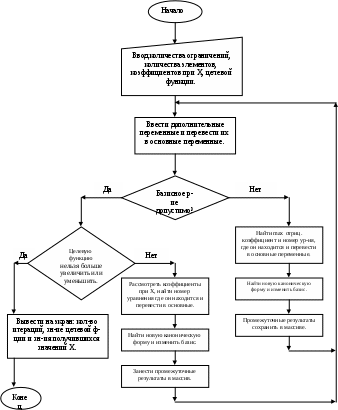
Рисунок 1 – Представление симплекс-метода в виде блок-схемы
2. ПРОЕТИРОВАНИЕ ПК ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ
2.1 Тестовый вариант решения задачи линейного программирования симплекс-методом
Условие задачи: для изготовления цемента двух видов используется сырье трех видов. Запасы сырья известны и равны соответственно: 264, 136 и 266 т. Количество сырья каждого вида, необходимое для производства единицы цемента первоговида соответственно равны: 12, 4 и 3. Для цемента второго вида: 3, 5 и 14. Прибыль от реализации цемента первого вида составляет 6 у. е., от цемента второго вида – 4 у. е.

Найти максимальное значение целевой функции F(X) = 6x1 + 4x2.

Составить план, обеспечивающий наибольшую прибыль производству: 

– записать математическую модель; 

– решить задачу симплекс-методом; 

Решение: 

Математическая модель.

x1 – производство цемента первого вида; 

---

x2 – производство цемента второго вида;

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. 

Определим максимальное значение целевой функции F(X) = 6x1+4x2 при следующих условиях (ограничениях).
12x1 + 3x2 ≤ 264; 

4x1 + 5x2 ≤ 136 ;

3x1 + 14x2 ≤ 266.

Для построения первого опорного плана приведем систему неравенств к системе уравнений путем введения дополнительных переменных (переход к канонической форме). 
12x1 + 3x2 + 1x3 + 0x4 + 0x5 = 264;

4x1 + 5x2 + 0x3 + 1x4 + 0x5 = 136;

3x1 + 14x2 + 0x3 + 0x4 + 1x5 = 266.
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных:

 x3, x4, x5.

Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,264,136,266)
Таблица 2 – Первый опорный план в виде нулевой таблицы

План	Базис	В	x1	x2	x3	x4	x5
0	x3	264	12	3	1	0	0
	x4	136	4	5	0	1	0
	x5	266	3	14	0	0	1
Индексная строка	F(X0)	0	-6	-4	0	0	0

Переходим к основному алгоритму симплекс-метода.
Таблица 3 – Первая симплекс-таблица

План	Базис	В	x1	x2	x3	x4	x5	min
1	x3	264	12	3	1	0	0	22
	x4	136	4	5	0	1	0	34
	x5	266	3	14	0	0	1	88.67
Индексная строка	F(X1)	0	-6	-4	0	0	0	0

---

Итерация №0.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. 

Вычислим значения Di по строкам как частное от деления

 и из них выберем наименьшее:  

Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен 12 и находится на пересечении ведущего столбца и ведущей строки. Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 1 войдет переменная x1. Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x3плана 0 на разрешающий элемент, равный 12. На месте разрешающего элемента в плане 1 получаем 1. В остальных клетках столбца x1 плана 1 записываем нули. Таким образом, в новом плане 1 заполнены строка x1 и столбец x1 . Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент 12

НЭ = СЭ - (А*В)/РЭ , где
СТЭ – элемент старого плана, РЭ – разрешающий элемент (12), А и В – элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. 
Таблица 4 – Вторая симплекс-таблица

План	Базис	В	x1	x2	x3	x4	x5	min
2	x1	22	1	0.25	0.0833	0	0	88
	x4	48	0	4	-0.3333	1	0	12
	x5	200	0	13.25	-0.25	0	1	15.09
Индексная строка	F(X2)	132	0	-2.5	0.5	0	0	0

---

Итерация №1.

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления и из них выберем наименьшее:
 
Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен 4 и находится на пересечении ведущего столбца и ведущей строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 2 войдет переменная x2 . Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x4 плана 1 на разрешающий элемент РЭ=4. На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x2 плана 2 записываем нули. 

Таким образом, в новом плане 2 заполнены строка x2 и столбец x2 . Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Конец итераций: индексная строка не содержит отрицательных элементов – найден оптимальный план.
Таблица 5 – Окончательный вариант симплекс-таблицы

План	Базис	В	x1	x2	x3	x4	x5
3	x1	19	1	0	0.1042	-0.0625	0
	x2	12	0	1	-0.0833	0.25	0
	x5	41	0	0	0.8542	-3.31	1
Индексная строка	F(X3)	162	0	0	0.2917	0.625	0

Оптимальный план можно записать так:
x1 = 19; x2 = 12;

F(X) = 6*19 + 4*12 = 162.
3. РАЗРАБОТКА ПК ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ
3.1 Выбор языка программирования и среды разработки ПК для решения задач линейного программирования симплексным методом

---

Смотрите также файлы

• Qrs комплексіні V.doc

• Общие методические указания Учебная дисциплина Криминология и предупреждение преступлений.docx

• Р ецензия на лабораторную работу 2 по дисциплине Объектноориентированное программирование 2 студента фдо тусур.doc

• Максаты бжб жне тжб нтижелерін талдау.docx

• Руководство по установке Внимание! 81. 4 ставятся только на 81 81. 1 81. 3).doc