Файл: Сборник задач по высшей математике. 1 курс с контрольными работами. М. Айрис Пресс. 2009.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 22
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ДЗ за 2 семестр КТО-223, КТО-224
1 занятие. Частные производные первого и второго порядков. Полный дифференциал функции двух переменных. Дифференцирование сложной и неявно заданной функции. Производные высших порядков
Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс: с контрольными работами. М. Айрис Пресс. 2009.
Номера: 11.3.9, 11.3.10. 11.3.18, 11.4.2 – ознакомиться,
11.3.30, 11.3.31, 11.3.32, 11.3.47, 11.3.49, 11.4.4, 11.4.22, 11.5.59
Найти частные производные данных функций по каждой из независимых переменных
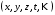 и полный дифференциал:
и полный дифференциал:11.3.30.
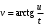 . 11.3.31
. 11.3.31 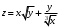 . 11.3.32.
. 11.3.32. 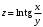 .
. Вычислить приближённо:
11.3.47.
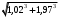 . 11.3.49.
. 11.3.49. 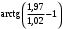 .
. 11.4.4. Найти
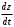 , если
, если 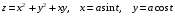 .
.11.4.22. Найти производную
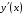 неявной функции, заданной уравнением
неявной функции, заданной уравнением 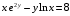 .
.11.5.59. Вычислить первые, вторые и третьи частные производные для функции
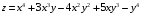 .
.2 занятие. Производная по направлению. Градиент. Экстремум функции 2-х переменных
1. Найти производную функции
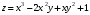 в точке
в точке 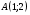 по направлению от точки
по направлению от точки 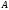 к точке
к точке 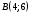 . Определить направление и величину максимального роста данной функции в данной точке.
. Определить направление и величину максимального роста данной функции в данной точке.2. Найти производную функции
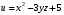 в точке
в точке 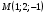 по направлению от этой точки к точке
по направлению от этой точки к точке 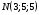 .
.Исследовать на экстремум следующие функции:
| 3. 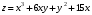 | 4. 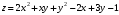 |
Ответы
| 1. 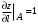 , , 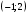 , , 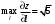 | 2. 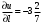 |
| 3. 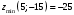 , в , в 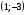 нет экстр нет экстр | 4. 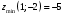 |
ИДЗ 1 «ФНП» (Контрольная работа 7) из методических указаний: Составители: Веснина А.А., Стругова Т.М., Назарук Е.М. Типовые расчёты по курсу «Высшая математика». II часть. ОмГТУ. 2011.
Задания: 3, 4, 6.
3 занятие. Наибольшее и наименьшее значение функции непрерывной в ограниченной замкнутой области.
Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс: с контрольными работами. М. Айрис Пресс. 2009.
11.7.32.
Найти наибольшее и наименьшее значение функции
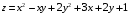
в замкнутой области
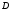 – треугольник, ограниченный осями координат и прямой
– треугольник, ограниченный осями координат и прямой 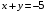 .
. 4 занятие. Двойной интеграл в декартовой системе координат
В двойном интеграле
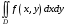 расставить пределы интегрирования двумя способами, если область
расставить пределы интегрирования двумя способами, если область 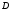 ограничена линиями:
ограничена линиями:| 1. | 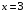 , ,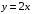 , ,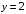 . . | 2. | 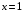 , ,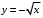 , ,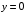 . . | 3. | 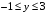 , ,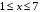 . . |
4. Изменить порядок интегрирования
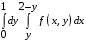 .
.5. Вычислить двойной интеграл
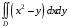 , где область
, где область  ограничена линиями:
ограничена линиями: 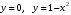 .
. 5 занятие. Двойной интеграл в полярной системе координат
1. Перейти к полярной системе координат и расставить пределы интегрирования в двойном интеграле
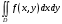 , если
, если 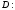 а)
а) 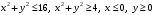 ;
;б)
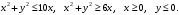
2. Найти массу пластинки, имеющей форму четверти круга радиуса 2, если известно, что
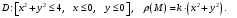
6 занятие. Приложения двойного интеграла
1. Найти массу пластины
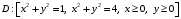 с поверхностной плотностью
с поверхностной плотностью 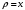 .
.2. Найти координаты центра масс пластины
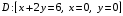 , если поверхностная плотность
, если поверхностная плотность 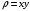 .
.8 занятие. Криволинейный интеграл II рода. Работа
1. Найти работу переменной силы
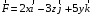 перемещения материальной точки по отрезку
перемещения материальной точки по отрезку 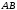 от
от 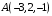 до
до 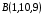 .
. 2. Найти работу переменной силы
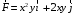 перемещения материальной точки по дуге
перемещения материальной точки по дуге 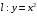 от
от 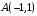 до
до 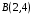 .
.9 занятие. Криволинейный интеграл второго рода
-
Вычислить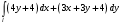 по различным путям, соединяющим точки
по различным путям, соединяющим точки 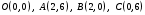 : а)
: а) 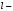 отрезок
отрезок 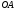 , б)
, б) 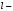 ломаная
ломаная 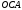 , в)
, в) 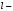 ломаная
ломаная 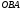 , г)
, г) 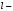 дуга
дуга 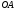 параболы
параболы 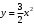 .
. -
Вычислить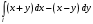 двумя способами, где
двумя способами, где 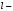 граница
граница 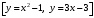 .
.
-
занятие. ДУ первого порядка: с разделяющимися переменными, однородные
линейные и Бернулли
Найти общее решение ДУ: 1)
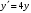 , 2)
, 2) 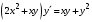 .
.3)
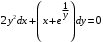 , (линейное относительно
, (линейное относительно  ), 4)
), 4) 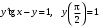 .
.-
занятие. ДУ высших порядков, допускающие понижение порядка
1)
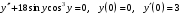 , 2)
, 2) 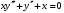 ,
, -
занятие. Линейные однородные и неоднородные ДУ с постоянными коэффициентами
1)
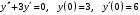 , 2)
, 2) 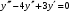 , 3)
, 3) 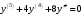 ,
, 4)
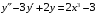 , 5)
, 5) 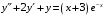 .
.-
занятие. Линейные неоднородные ДУ с постоянными коэффициентами
1)
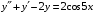
Лунгу К,Н., Норин В,П., Письменный Д.Т., Шевченко Ю.А. «Сборник задач по высшей математике» – 2009.
Номера: 2.7.58, 2.7.73