ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.12.2021
Просмотров: 61
Скачиваний: 1
Лекція №8
Тема: Лінійчаті розгорні поверхні.
Питання:
-
Торсові поверхні. Утворення. Ортогональні проекції.
-
Поверхні паралельного переміщення. Утворення. Графічні моделі.
1. Лінійчаті поверхні з однією напрямною (торси). В групу входять поверхні з ребром звороту, циліндрична поверхня, конічна поверхня. Торсом називають поверхню, над якою можна здійснити процес суміщення всіма її точками з площиною без складок та розривів. Такі поверхні ще називають розгортними поверхнями. Характерною ознакою розгортних поверхонь є те, що їх прямолінійні твірні перетинаються. Розгортну лінійчату поверхню можна уявити собі як граничний стан гранної поверхні з гранями, ширина яких наближається до нуля. Тому така поверхня може бути, як багатогранник, розгорнута на площину. В загальному вигляді розгортна поверхня утворюється як неперервна множина дотичних {ℓі } до просторової кривої лінії a і називається торсом (рис. 5.8).
Рисунок 5.8 - Формоутворення торсової поверхні загального вигляду
Криву a називають ребром звороту торса.
Найпростішими окремими випадками торса є конічна і циліндрична поверхні, у яких ребро звороту стягується в точку. У конічній поверхні, яка показана на рис. 5.9, а, це точка S – його вершина, у циліндричній поверхні (див. рис. 5.9, б – нескінченно віддалена точка перетину прямолінійних твірних S∞.
а) б)
Рисунок 5.9 - Окремі випадки торсових поверхонь
Плоску криву m (див. рис. 5.8 та рис. 5.9), яка утворюється внаслідок перерізу торсових поверхонь площиною, називають напрямною лінією.
Визначник цієї групи поверхонь має вигляд:
Defθ = (ℓ, а) [A],
де [A] – алгоритмічна частина, яка містить умову, що твірна ℓ при русі торкається ребра звороту а, або його перетворень у вигляді точок S та S∞.
Для задання торсової поверхні загального вигляду на прямокутних проекціях достатньо задати відповідні проекції її визначника - ребра звороту n (n1,n2) та побудувати сукупність прямокутних проекцій прямих, що утворюють лінійчатий каркас поверхні, показаної на рис. 5.10.
Рисунок 5.10 -Утворення прямокутних проекцій торсової поверхні загального вигляду
Рисунок 5.11 - Утворення прямокутних проекцій еліптичного конуса
Якщо як напрямну лінію m прийняти замкнуту плоску криву, то тіло, обмежене циліндричною поверхнею, має назву циліндра, який показано на рис. 5.12.
Рисунок 5.12 - Утворення прямокутних проекцій еліптичного циліндра
3. Поверхні паралельного переміщення. В групу таких поверхонь входять поверхні, що утворюються внаслідок поступального руху твірної лінії ℓ, одна з точок якої переміщується вздовж напрямної лінії m, а всі інші здійснюють паралельне переміщення. Визначник поверхонь паралельного переміщення, яка показана на рис. 5.13, має вигляд:
Defθ = (ℓ, m) [A],
де [A] – алгоритмічна частина, яка складається з умови паралельного переміщення точок твірної ℓ .
Рисунок 5.13 - Формоутворення поверхні паралельного переміщення
На прямокутних проекціях поверхні паралельного переміщення задають у вигляді проекцій їх визначника: сукупності відповідних проекцій напрямної лінії та твірних ліній. На рис. 5.14 показана поверхня паралельного переміщення, утворена незамкненою кривою лінією ℓ.
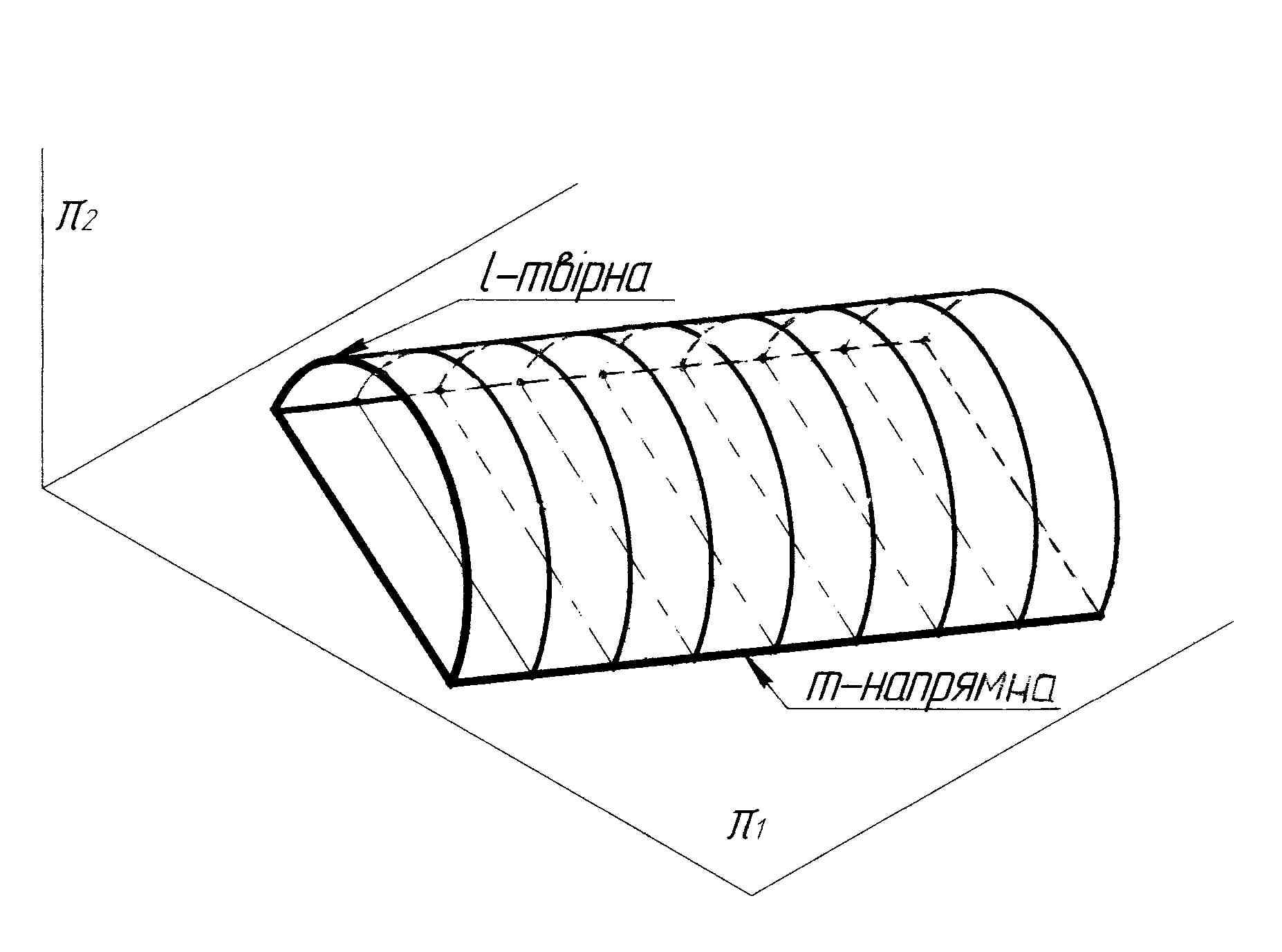
Рисунок 5.14 - Утворення прямокутних проекцій поверхні паралельного переміщення
Поверхня паралельного переміщення може бути утворена замкненою кривою лінією. Таку поверхню, приклад якої показано на рис. 5.15, відносять до класу каналових поверхонь.
Рисунок 5.15 - Утворення прямокутних проекцій поверхні паралельного переміщення з замкненою твірною лінією
Питання які виносяться на СРС:
-
побудова перерізів поверхонь переносу площинами окремого положення;
-
побудова проекцій наскрізних отворів в поверхнях переносу.
Література – основна (С. 77-84) [8] (С.40-50) [9];
- додаткова (С. 5-46) [15].