ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2021
Просмотров: 125
Скачиваний: 1
Будівельна механіка в прикладах і задачах
Спеціальність – 0921 – “Будівництво”
Тема: Статично визначена ферма
Лекція №3. Розрахунок статично визначеної ферми на сталі навантаження та побудова ліній впливу .
Мета і задачі:
Метою теми є вміння визначати напружений стан в стержнях статично визначеної ферми – конструкції для перекриття значних прольотів, в яких балкою перекрити не раціонально.
Для досягнення мети необхідно вирішення наступних задач:
1. Збір навантаження.
2. Визначення реакцій в опорах від:
дії власної ваги,
дії снігового
навантаження зліва (одностороннє
снігове
навантаження дає екстремальні зусилля в стержнях ферми),
дії Р = 1, прикладеного
до шуканого напрямку переміщення.
3. Графічний розрахунок зусиль в стержнях ферми від дій вказаних навантажень (побудова діаграм Максвела - Кремони).
4. Складання таблиці зусиль в стержнях ферми від дії власної ваги, снігового навантаження та визначення переміщення середини нижнього поясу (максимального переміщення по вертикалі).
5. Побудова ліній впливу в 3-х стержнях ферми та визначення зусиль за лініями впливу.
6. Порівняння даних аналітичного розрахунку зусиль в 3–х стержнях з розрахунком за лініями впливу.
3.1 Розрахунок статично визначеної ферми на сталі навантаження.
http://www.youtube.com/watch?v=KCFAcPiyY9I&NR=1 Область
практичного впровадження ферм
2В-3,
де В – число вузлів.
(3.1)
Шарнірне з’єднання стержнів в розрахунковій схемі ферм забезпечує рівність нулю згинального моменту М, перша похідна від еп. М – поперечна сила Q теж дорівнюватиме нулю. Із внутрішніх зусиль в фермі залишаються подовжені сили N. До розрахункової схеми ферм навантаження прикладаються лише в вигляді зосереджених сил в вузлах, розподілені навантаження (власна вага, сніг, вітер) приводяться до зосереджених сил в вузлах. При великій кількості стержнів в фермі раціональним є графічний метод визначення зусиль в стержнях ферми (побудова діаграм Максвела-Кремони). Побудова діаграми розпочинається із визначення складових опорних реакцій за рівняннями статики та позначення зовнішніх та внутрішніх полів. Зовнішні поля – це проміжок між зовнішніми зосередженими силами та знайденими реакціями, внутрішні поля – проміжки між складовими елементами ферми. Нумерація полів – зліва направо. Таким чином, кожна сила та стержень ферми отримує назву. Розрахунки ведуться в табличній формі, в якій стержні ферми матимуть вже свою назву. Наступним етапом розрахунку є побудова багатокутника зовнішніх сил, який має бути замкненим, оскільки ферма має бути в рівновазі. Для цього в напрямку зліва направо за годинниковою стрілкою відкладаються в масштабі зовнішні сили та реакції. Потім проводиться пошук вузла, де зходиться не більше двох невідомих стержнів, та стержні, що входять до нього, розглядаються за годинниковою стрілкою . Обхід вузлів продовжується до останнього.
При дії на ферму симетричного навантаження можна обмежитись розглядом половини вузлів, оскільки зусилля в симетричних стержнях будуть такі ж самі.
3.1.1
Розрахунок
ферми на власну вагу
.
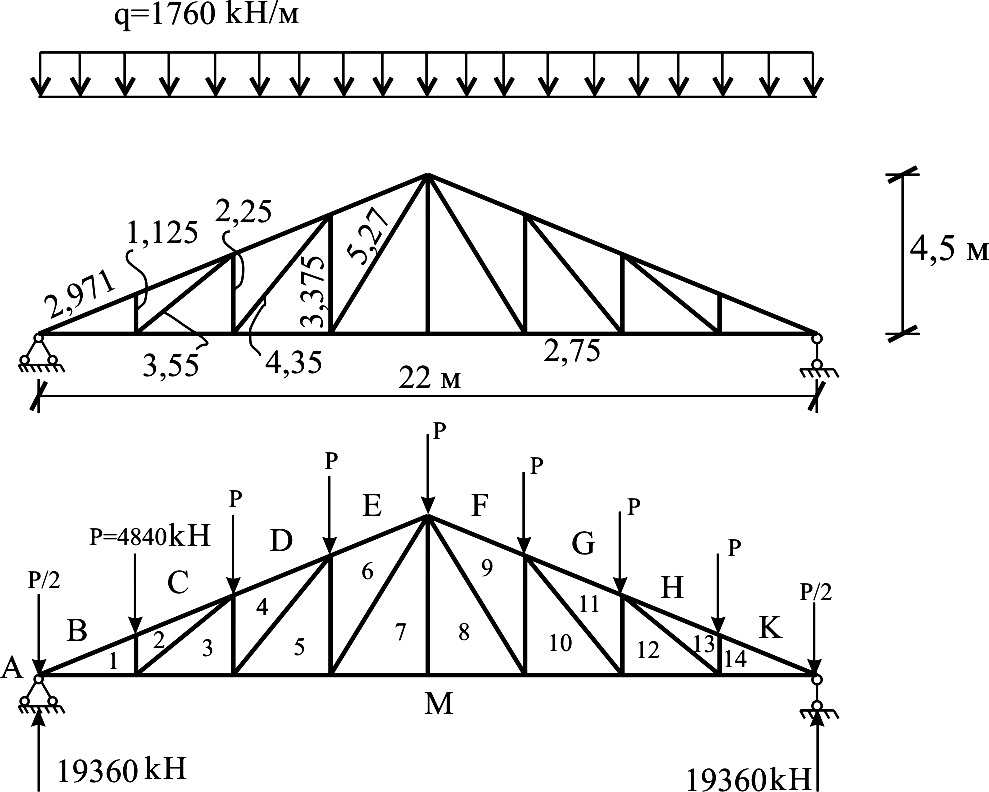

Рисунок 3.1 – Розрахункова схема, навантаження та реакції в фермі від дії власної ваги
-
Розрахунок дії снігового навантаження зліва
Одностороння дія снігового навантаження викликає в елементах ферми більші зусилля, ніж наявність снігу на обидвох її сторонах. Саме тому при дії снігу розглядається односторонній його вплив.
Рисунок 3.2 – Розрахункова схема, навантаження та реакції в фермі від дії снігу зліва
3.1.3 Визначення переміщення середини нижнього поясу ферми
Рисунок 3.3 – Розрахункова схема, навантаження та реакції в фермі від дії одиничної сили за шуканим напрямком
-
Побудова діаграм Максвела - Кремони
Рисунок 3.4 – Діаграма Максвела – Кремони від дії одиничної сили Р=1 за шуканим напрямком переміщення середини нижнього поясу
Рисунок 3.5 – Діаграма Максвела – Кремони від дії власної ваги ферми
Рисунок 3.6 – Діаграма Максвела – Кремони від дії снігу на лівій половині ферми
-
Компонування таблиці зусиль в фермі
Таблиця 3.1
|
Назва стержня |
li м |
EАi |
Np kн |
N1 |
Nсніг |
|
|
|
Верхній пояс |
NB-1 NC-2 ND-4 NE-6 NF-9 NG-11 NH-13 NK-14 |
2,971 - - - - - - 2,971 |
1,5EА - - - - - - - |
-45280 -45280 -38621 -31963 -31963 -38621 -45280 -45280 |
-1.35 -1.35 -1.35 -1.35 -1.35 -1.35 -1.35 -1.35 |
-20700 -20700 -16200 -12300 -9400 -9400 -9400 -9400 |
109095 109095 93052 77008 77008 93052 109095 109095 |
|
Нижній пояс |
N1-м N3-м N5-м N7-м N8-м N10-м N12-м N14-м |
2,75 - - - - - - 2,75 |
1,5EА - - - - - - 1,5EА |
42283 35258 29632 23472 23472 29632 35258 42283 |
+1.254 - - - - - - - |
19450 14100 11500 8700 8700 8700 8700 8700 |
87592 74488 61383 48624 48624 61383 74488 87592 |
|
Стояки |
N1-2 N3-4 N5-6 N7-8 N9-10 N11-12 N13-14 |
1,125 2,250 3,375 4,500 3,375 2,250 1,125 |
EА - - - - - - |
-5371 -6992 -9489 0 -9489 -6992 -5371 |
0 0 0 1 0 0 0 |
-3300 -4800 -6550 0 0 0 0 |
0 0 0 0 0 0 0 |
|
Розкоси |
N2-3 N4-5 N6-7 N8-9 N10-11 N12-13 |
3,55 4,35 5,27 5,27 4,35 3,55 |
- - - - - - |
7991 9655 11320 11320 9655 7991 |
0 0 0 0 0 0 |
5200 6100 7000 0 0 0 |
0 0 0 0 0 0 |
Переміщення середини нижнього поясу від
,
дії власної ваги:
3.2 Побудову ліній впливу в фермі проведено за методом моментної точки. Етапи цього методу: 1–через стержень, в якому потрібно побудувати л.в., проводиться перетин таким чином, щоб в нього попало 3 стержні, 2– точка перетину ліній дії двох інших стержнів, крім досліджувального, є моментною точкою зусилля в цьому стержні, 3–до знайденої моментної точки записується сума моментів лівих чи правих сил, зазвичай розглядається частина ферми, де менше сил. В отриманому аналітичному виразі невідомим слугує шукане зусилля. Згідно цього виразу будується лінія впливу.
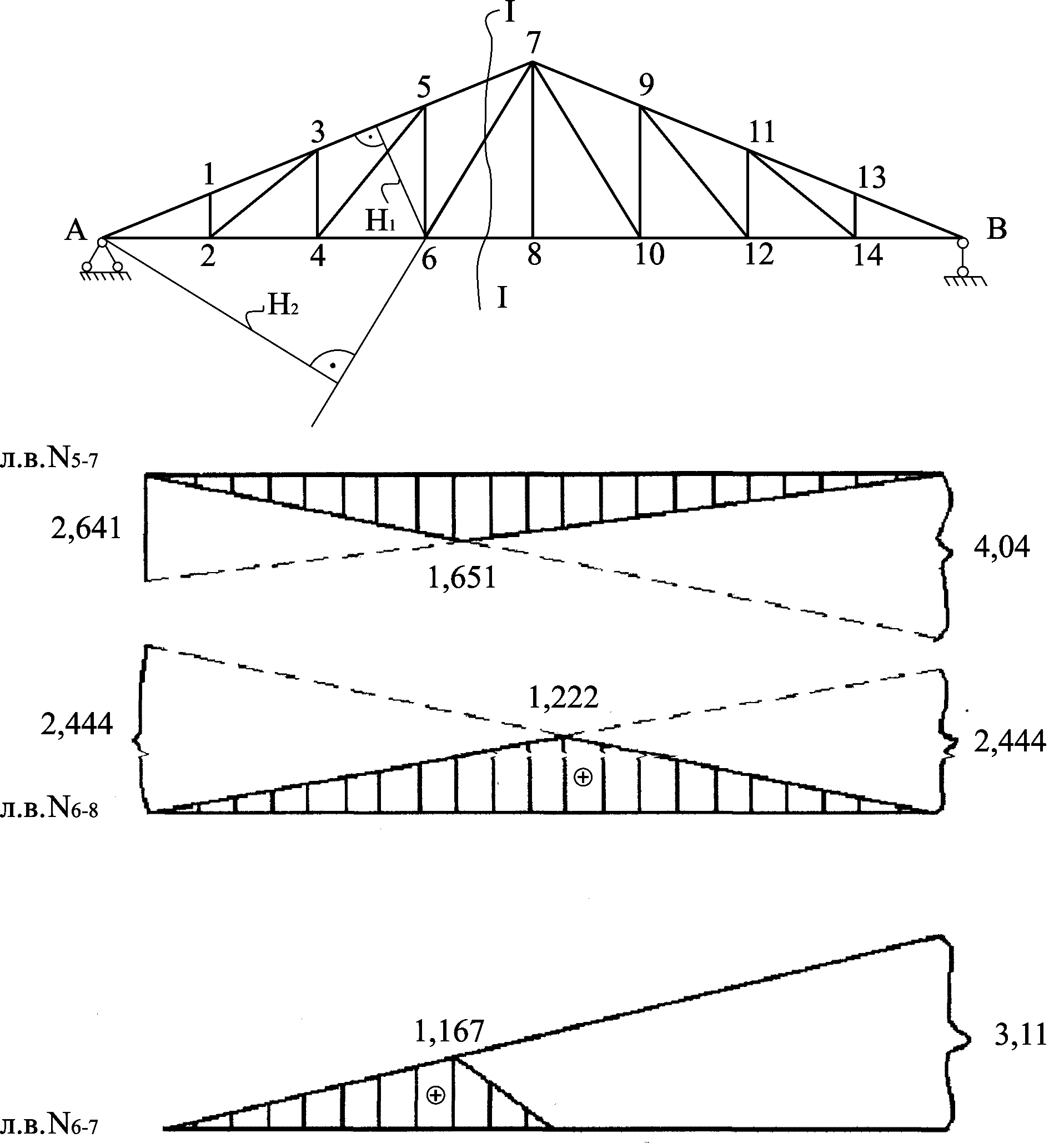
Рисунок 3.7 – Побудова ліній впливу поздовжніх сил в трьох стержнях ферми
-
Визначення зусиль в стержнях ферми за лініями впливу
проводиться
за формулою:
(3.2)
де
–
зовнішнє навантаження,
–
ордината л.в. під
.
N5-7
= 0.5*22м*1.651*1760кН/м = 31963,36кН
31963кН з графічного розрахунку.
N6-8
= 0.5*1.222*22м*1760кН/м = 23659кН
23472кН.
N6-7
= 0.5*1.167*11м*1760кН/м = 11297кН
11320кН.
Підсумок.
Після проходження даної лекції студент має вміти знаходити реакції в фермі, будувати еп. N, будувати лінії впливу та визначати за ними зусилля в фермі.
Контрольні питання.
1. Як перевірити геометричну незмінність ферми та статичну визначеність?
2.Як визначати реакції в фермі ?
3. Які зусилля виникають в розрахунковій схемі ферми?
4. Які основні принципи побудови діаграми Максвела-Кремони?
5. Що називають лінією впливу, як їх будувати та як визначати за ними
зусилля в фермах?
Джерела інформації.
1. Баженов В.А., Іванченко Г.М., Шишов О.В. Будівельна механіка. Розрахункові вправи. Задачі. Компютерне тестування.-К.: “Каравелла”, 2006.-344с.
2. Баженов В.А., Гранат С.Я., Шишов О.В. Будівельна механіка. Компютерний курс.-К.: Вища школа, 1999.-540с.
3. Баженов В.А. Будівельна механіка.-К.: Вища школа, 2000.-670с.
4. Бутенко Ю.Н. Строительная механика. – К.:”Вища школа”, 1989,- 480с.
5. Бутенко Ю.И. Строительная механика. Руководство к практическим занятиям. - К.: Вища школа, 1984.- 327 с
6. Дарков А.В. Шапошников Н.Н. Строительная механика. - М.:”Высшая школа”, 1986,-607с.
7. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем). – М.:”Высшая школа”, 1980, -384с.
8. Моргун А.С. Теорія споруд, ч. ІІІ, Будівельна механіка – Вінниця:
ВДТУ,1997,90 с.
9. Моргун А.С. Практикум з будівельної механіки. – Вінниця: ВДТУ, 1997,90 с.
10. Піскунов В.Г. Опір матеріалів з основами теорії пружності і пластичності. Ч.І. Книга 3. Опір дво- і тривимірних тіл. - К.: Вища школа, 1995.- 272 с.
Глосарій.
1.Геометрична незмінність –деформації елементів можливі лише в результаті прикладення навантаження.
2. Статична визначеність – внутрішні зусилля можна знайти лише з рівнянь статики.
3. Лінія впливу – графік, що показує закон зміни досліджувального фактора (згинального моменту, поперечної сили, реакції, подовженої сили) в залежності від положення на балці рухомого одиничного навантаження Р=1.