Файл: Исследование операций и методы оптимизации Заданиевариант 2 Выполнена обучающимся группы о. Издтв 23. 1Б22.docx

Ситуация 1

Предположим, что Бычкову надо принять два решения, причем второе решение зависит от исхода первого. Прежде чем создать новое производство. Бычков намерен заказать исследование рынка и заплатить за него 10 тыс. руб. Результаты этого исследования могли бы помочь решить вопрос о том, следует ли создавать большое производство, малое производство или не делать ничего. Бычков понимает, что такое обследование рынка не может дать достоверную информацию, но может тем не менее оказаться полезным.

Вопрос: Следует ли проводить обследование рынка?

Решение:

На рис. 1 показаны возможные состояния среды и решения, а также вероятности различных результатов обследования и вероятности наступления различных состояний среды. (Прямоугольники используются для обозначения вершин принятия решений, кружочки обозначают неконтролируемые события — наступление состояний среды.)

Дерево решений Бычкова с рассчитанными EMV представлено на рис. 2. Короткими параллельными линиями отсекается та ветвь, которая оказывается менее благоприятной по сравнению с другими и может быть отброшена.

Ожидаемая стоимостная оценка наилучшего решения в случае, если будет заказано обследование рынка, составляет 49,2 тыс. руб., без обследования она составляет 40 тыс. руб.

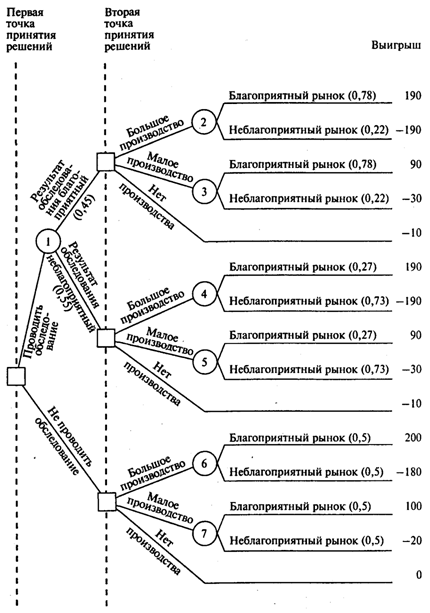
Рисунок 1- Первое дерево решений

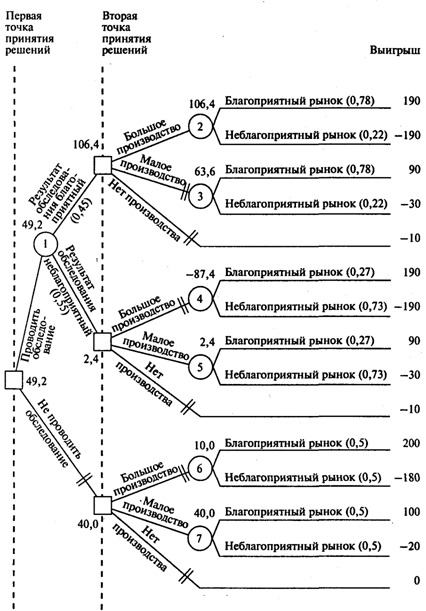
Рисунок 2- Второе дерево решений

Ответ: Да, следует заказывать обследование рынка. Если результат обследования будет благоприятным, следует создавать большое производство, если неблагоприятным — малое.

Ситуация 2

Создание нового напитка в условиях конкуренции.

Фирма «Напитки для дома» разрабатывает, производит и продает смеси для безалкогольных коктейлей и приготовляет напитки для домашнего потребления.

Миссис Ли, руководитель отдела развития фирмы, сообщила президенту, мистеру Робину Свану, что эксперименты в отделе развития указывают на возможность создания напитка «PINA-cola» на основе нового метода переработки кокосов. Миссис Ли порекомендовала начать программу по производству «PINA-cola». Она оценила в 100 тыс. долл. стоимость исследовательских работ по созданию этого напитка и отметила, что на эту работу потребуется один год. В беседе с мистером Сваном миссис Ли оценила в 90% возможность успешного завершения работы ее специалистами. Она также оценила как 0,8 вероятность разработки в течение 12 месяцев аналогичного напитка конкурирующей фирмой.

Мистер Сван заинтересовался возможными объемами продаж такого напитка. Он переговорил с мистером Беснеттом, занимающимся внедрением новых продуктов на рынок. Тот сообщил, что продавать «PINA-cola» можно, но объем продаж зависит от того, как его примут бакалейные и винные магазины. Судя по отчетам о продажах, другие производители также работают над созданием напитков из тропических фруктов. Если какая-либо фирма создаст аналогичный напиток, рынок, разумеется, будет поделен между двумя фирмами. Мистер Сван попросил мистера Беснетта дать оценки будущих продаж и ожидаемой приведенной прибыли при различных вариантах рыночной конъюнктуры.

Мистер Беснетт представил следующие данные:

В данных мистера Беснетта не учтены издержки на разработку, новое оборудование и внедрение «PINA-cola» на рынок. Ожидается, что издержки на новое оборудование составят 100 тыс. долл., так как кокосы требуют специальной обработки. Издержки, связанные с выходом на рынок, составят 150 тыс. долл., так как потребуется телевизионная реклама.

Миссис Ли отметила, что кроме альтернатив «ничего не предпринимать» и «проводить полномасштабную программу исследований» она может предложить еще два варианта действий:

1. Неспешно проводить исследования в течение 8 месяцев, чтобы посмотреть, выйдет ли какая-нибудь другая фирма на рынок с аналогичным продуктом, а если нет - развить бешеную скорость работ. Замедленная программа исследований на следующие 8 месяцев обойдется в 10 тыс. долл. в месяц, т.е. в 80 тыс. долл. Вероятность успешного завершения этой программы та же, что и при полномасштабных исследованиях. Вероятность того, что конкуренты в течение 8 месяцев создадут аналогичный продукт, равна 0,6. Интенсивные исследования могут быть проведены в течение 4 месяцев (с 9-го по 12-й) и обойдутся еще в 60 тыс. долл. Они будут проводиться только в том случае, если результаты исследований первых 8 месяцев окажутся успешными. Вероятность успеха в целом равна 0,9. Эта программа получила название восьмимесячной.

2. Шесть месяцев проводить исследования, требующие затрат 10 тыс. долл. в месяц, и предпринять разведку действий конкурентов, чтобы определить, ведутся ли разработки аналогичного продукта. Если кто-то разработает продукт через 6 месяцев, потребуется лишь 30 тыс. долл. для того, чтобы провести его анализ и скопировать продукт. Если конкурирующий продукт не будет создан, то при общих затратах в 120 тыс. долл. он будет разработан фирмой «Напитки для дома» с вероятностью 0,9. Вероятность того, что за 6 месяцев будет разработан конкурирующий продукт, равна 0,5. Эта программа получила название шестимесячной.

Мистеру Беснетту, разумеется, не хотелось бы выходить на рынок вслед за конкурентом. Ему известно, что первый продукт обычно завоевывает большую часть рынка. Если на рынок выйдет конкурирующая фирма, можно получить только 50% прибыли, указанной в таблице.

Задание:

Какой из следующих вариантов действий вы порекомендуете, рассматривая критерий максимизации ожидаемой стоимостной оценки альтернатив:

1) полномасштабные исследования;

2) восьмимесячная программа замедленных исследований с последующим их ускорением;

3) шестимесячная программа замедленных исследований и изучение поведения конкурентов;

4) ничего не предпринимать.

Обоснуйте вывод, нарисовав дерево решений и проведя соответствующие расчеты.

Решение:

Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков.

Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока.

Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника.

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.

1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки B1 B2 a = min(Ai)

A1 0.1 800 0.1

A2 0.6 600 0.6

A3 0.3 500 0.3

b = max(Bi) 0.6 800

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 0.6, которая указывает на максимальную чистую стратегию A2.

Верхняя цена игры b = min(bj) = 0.6.

Седловая точка (2, 1) указывает решение на пару альтернатив (A2,B1). Цена игры равна 0.6.

Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы.
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B₁	B₂	a = min(A_i)
A₁	0.1	800	0.1
A₂	0.6	600	0.6
A₃	0.3	500	0.3
b = max(B_i)	0.6	800

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 0.6, которая указывает на максимальную чистую стратегию A₂.
Верхняя цена игры b = min(b_j) = 0.6.
Седловая точка (2, 1) указывает решение на пару альтернатив (A2,B1). Цена игры равна 0.6.
2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.
Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если a_ij ≥ a_kj для всех j Э N и хотя бы для одного j a_ij > a_kj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.
Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M a_ij ≤ a_il и хотя бы для одного i a_ij < a_il. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.
Стратегия A₂ доминирует над стратегией A₃ (все элементы строки 2 больше или равны значениям 3-ой строки), следовательно, исключаем 3-ую строку матрицы. Вероятность p₃ = 0.

0.1	800
0.6	600

В платежной матрице отсутствуют доминирующие столбцы.
Мы свели игру 3 x 2 к игре 2 x 2.
Чтобы представить числа целыми, умножим элементы матрицы на 10 и вычтем 0. Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана).

1	8000
6	6000

3. Находим решение игры в смешанных стратегиях.
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях (для игрока II):
x₁+6x₂ ≥ 1
8000x₁+6000x₂ ≥ 1
F(x) = x₁+x₂ → min
найти максимум функции Z(y) при ограничениях (для игрока I):
y₁+8000y₂ ≤ 1
6y₁+6000y₂ ≤ 1
Z(y) = y₁+y₂ → max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.