Файл: Исследование операций и методы оптимизации Заданиевариант 2 Выполнена обучающимся группы о. Издтв 23. 1Б22.docx

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1 расположена в столбцах дополнительных переменных.
Тогда X = C*A^-1 =

(0, 1) x

1 -1/6 0 1/6

= (0;1/6)

Оптимальный план двойственной задачи равен:
x₁ = 0, x₂ = ¹/₆
F(X) = 1*0+1*¹/₆ = ¹/₆
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
q_i = g*y_i; p_i = g*x_i.
Цена игры: g = 1 : ¹/₆ = 6
p₁ = 6*0 = 0
p₂ = 6*¹/₆ = 1
Оптимальная смешанная стратегия игрока I: P = (0; 1)
q₁ = 6*¹/₆ = 1
q₂ = 6*0 = 0
Оптимальная смешанная стратегия игрока II: Q = (1; 0)
Поскольку ранее элементы матрицы были умножены на число (10), то разделим цену игры на это число.
6 / 10 = ³/₅
Цена игры: v=³/₅
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑a_ijq_j ≤ v
∑a_ijp_i ≥ v
M(P₁;Q) = (0.1*1) + (800*0) = 0.1 ≤ v
M(P₂;Q) = (0.6*1) + (600*0) = 0.6 = v
M(P;Q₁) = (0.1*0) + (0.6*1) = 0.6 = v
M(P;Q₂) = (800*0) + (600*1) = 600 ≥ v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Поскольку из исходной матрицы были удалены строки, то найденные векторы вероятности можно записать в виде:
P(0,1,0)
Q(1,0)



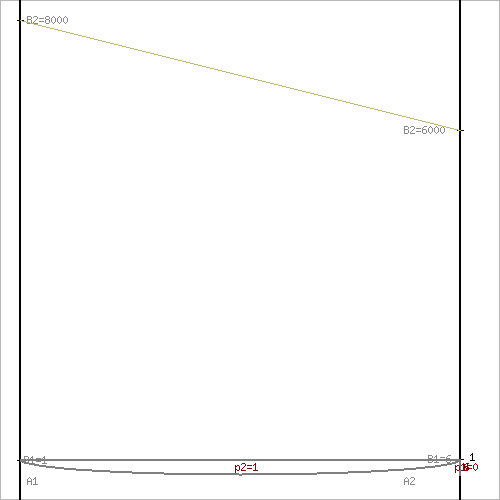
Решим задачу геометрическим методом, который включает в себя следующие этапы:

1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A1, правый - стратегии A2 (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S1 = (p1,p2).

2. На левой оси ординат откладываются выигрыши стратегии A1. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A2.

Решение игры (2 x 2) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.

---

Максиминной оптимальной стратегии игрока A соответствует точка N, для которой можно записать следующую систему уравнений:

p1 = 0

p2 = 1

Цена игры, y = 6

Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений

q1 = 1.

q2 = 0.

Ситуация 3

Выбор оборудования для производства нового продукта.

Компания Cail создала новое кожаное изделие и сейчас разрабатывает пятилетний план производства и продажи этого продукта. Госпожа Хедрич, президент компании, поручила разработку этого проекта своему ассистенту, Каролине Гарсия. Она должна координировать работу директора компании по продажам Барбары Гвирола и управляющего производством Карен Хоуп.

Компания Cail - небольшая фирма, которая уже более 30 лет занимается производством изделий из кожи. Она приобретает выделанные шкуры и производит кошельки, ремни и сумочки. Новый продукт представляет собой комбинацию кошелька, портмоне для ключей и бумажника для кредитных карточек. Производственники разработали набор материалов для изготовления универсального портмоне. Они подсчитали, что в течение пяти лет стоимость материалов и накладные расходы составят 1,5 долл. на одно изделие при пятидневной рабочей неделе без сверхурочных.

Удельные затраты на труд и оборудование будут зависеть от того, какая машина будет использована для производства.

Аналитики свели проблему выбора к двум типам специализированного оборудования. Первый тип - полуавтоматическая машина, которая не обеспечивает раскрой материала, но может сшивать его, вшивать молнии и заклепки и обеспечивать два типа дизайна продукта. Стоимость машины 450 тыс. долл. Средние переменные издержки на труд и прочие издержки, связанные с использованием этого оборудования, составляют 2,5 долл. Производительность такого оборудования - 640 шт. в день. При этом затраты времени на наладку и ремонт оборудования составляют 12,5% (¹/₈ общего времени).

Вторая машина, которая может использоваться при изготовлении продукта, является автоматом. Она позволяет кроить и сшивать материал, вшивать молнии и заклепки, делать портмоне с дизайном трех типов. Эта машина стоит 850 тыс. долл. Средние переменные издержки при ее использовании составляют 1,75 долл. Этот тип оборудования имеет более высокую производительность - 800 шт. в день. Затраты времени на наладку и ремонт машины ввиду ее сложности также более высокие - 25% (

---

¹/₄ времени).

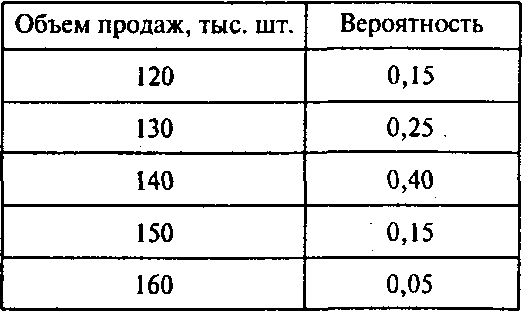
Анализ продаж не позволил получить точные результаты. Объем продаж на ближайшие пять лет в значительной степени зависит от оценок производственных издержек и производительности. Однако госпожа Гвирола при поддержке госпожи Хедрич определила наиболее вероятную цену нового портмоне в 6 долл. Такая цена позволяет новому изделию конкурировать с другими подобными продуктами на рынке. Постепенно новое изделие может вытеснить конкурентов с рынка, так как оно имеет лучшие потребительские свойства. Оценка среднего объема продаж нового портмоне - около 140 тыс. шт. в год. Анализ объема продаж этого изделия - сложная задача, так как новый продукт значительно отличается от других, предлагаемых на рынке в настоящее время. Оценки годового объема продаж продукта по цене 6 долл. с указанием соответствующих вероятностей приведены в следующей таблице:



Эти оценки и значения вероятностей верны для каждого года пятилетнего периода планирования. Используя оценки продаж и данные о мощностях оборудования, компания должна решить, как поступить, если спрос превысит производительность оборудования. В этом случае можно модифицировать оборудование и увеличить его производительность. Другой путь - использовать сверхурочное время. Оплата сверхурочного времени приведет к увеличению средних издержек на 1,2 долл. для полуавтоматической машины и на 0,9 долл. для автоматической машины.

Модификацию оборудования можно провести в конце нового года. В этом случае использование сверхурочного времени может потребоваться только в первом году.

Затраты на модификацию полуавтоматической машины до производительности, обеспечивающей максимальный объем продаж, составляют 60 тыс. долл. Затраты на модификацию автомата составляют 70 тыс. долл. Госпожа Хедрич дала указание использовать в расчетах процент на капитал, равный 15%, и 50-недельную продолжительность производственного года.

Задания:

1. Используйте дерево принятия решений и, основываясь на критерии максимизации ЕМУ, определите, какую машину следует выбрать компании. Следует ли проводить модификацию оборудования или лучше прибегнуть к использованию сверхурочного времени?

2. Изменится ли ваше решение в пункте 1, если известно, что остаточная стоимость полуавтоматической машины в конце пятилетнего периода составляет 90 тыс. долл., а автоматической машины - 170 тыс. долл.?

---

3. Постройте платежную матрицу для указанных объемов продаж (предположите, что модификация машин невозможна и может быть использовано только сверхурочное время). Предположите, что вероятности соответствующих объемов продаж неизвестны. Какую машину следует выбрать компании (с учетом стоимости оборудования, но без учета остаточной стоимости) по следующим критериям:

а) maximax;

б) maximin;

в) критерий безразличия.

Решение:

Исходные данные:

120	0.15
130	0.25
140	0.40
150	0.15
160	0.05

---

Критерий максимакса.
Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.

Ai	П1	П2	max(aij)
A1	120	0.15	120
A2	130	0.25	130
A3	140	0.40	140
A4	150	0.15	150
A5	160	0.05	160

Выбираем из (120; 130; 140; 150; 160) максимальный элемент max=160
Вывод: выбираем стратегию N=5.
Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) A_i, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(a_ijp_j)
∑(a_1,jp_j) = 120*0.5 + 0.15*0.5 = 60.075
∑(a_2,jp_j) = 130*0.5 + 0.25*0.5 = 65.125
∑(a_3,jp_j) = 140*0.5 + 0.40*0.5 = 70.2
∑(a_4,jp_j) = 150*0.5 + 0.15*0.5 = 75.075
∑(a_5,jp_j) = 160*0.5 + 0.05*0.5 = 80.025

Ai	П1	П2	∑(aijpj)
A1	60	0.075	60.075
A2	65	0.125	65.125
A3	70	0.2	70.2
A4	75	0.075	75.075
A5	80	0.025	80.025
pj	0.5	0.5

---