ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 96
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема: « Правильные многогранники»
Геометрия 10 класс.
Цель урока: Познакомить учащихся с новым типом выпуклых многогранников – правильными многогранниками.
Задачи урока:
-
Обучающие: Ввести понятие правильного многогранника, рассмотреть свойства правильных многогранников.
-
Развивающие: Формирование пространственных представлений учащихся. Формирование умения обобщать, систематизировать, видеть закономерности. Развитие монологической речи учащихся.
-
Воспитательные: Воспитание эстетического чувства. Воспитание умения слушать. Формирование интереса к предмету.
Оборудование: Мультимедийный проектор, раздаточный материал (рабочие листы), демонстрационные модели многогранников, интернет.
glogster: http://www.glogster.com/dashboard/glogs/my
Прогнозируемый результат
-
Знать определение правильных многогранников. -
Уметь доказать, что существует всего пять видов таких тел. -
Уметь охарактеризовать каждый вид правильных многогранников. -
Знать теорему Эйлера (без доказательства).
Ход урока:
1. Организационный момент. Целевая установка урока (Сообщение темы, цели урока и порядка работы.) Раздел о правильных многогранниках носит описательный характер, на его изучение отводится два урок. Материал о правильных многогранниках существенно дополняет и логически завершает раздел «Многогранники». Фактически здесь продолжается классификация многогранников; из выпуклых многогранников выделяются правильные.
Учитель:Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности – от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книг о многогранниках.
В геометрии10 класса мы с вами изучили разные виды многогранников (вопрос к классу какие?): тетраэдр, параллелепипед, пирамиды, призмы. Но ни одно геометрическое тело не обладает такой красотой, как правильные многогранники, с которыми мы познакомимся на сегодняшнем уроке. Откройте тетради и запишите классная работа, тема « Правильные многогранники».
2. Актуализация знаний.
Сейчас давайте поиграем, перед вами рабочие листы.
Поставьте +, если верите, - если нет, справа (методика критического мышления).
1. Правильных многогранников много.
2. Правильные многогранники могут быть выпуклыми и не выпуклыми.
3. Для правильных многогранников действует эйлерова характеристика.
3. Одноклеточный организм феодарии (Circjgjnia icosahtdra) по форме напоминает правильный икосаэдр.
4. Кристаллы поваренной соли имеют форму куба;
5. Существует модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.
Посмотрите какие интересные вопросы, давайте в ходе нашего урока проверим, верно это или нет.
Давайте подумаем, что мы с Вами знаем о правильных многогранниках (использование методики критического мышления « Корзина»)
Задание: На доске висит корзинка, где условно собирается все, что дети знают по данной проблеме.
Методика: 1) учитель задает вопрос о том, что известно детям о поставленной проблеме;
2) каждый ученик самостоятельно вспоминает и записывает в тетрадь то, что он знает в этой связи (1-2 мин);
3) обмен информацией в парах;
4) каждая пара называет одно сведение или факт, не повторяя сказанного ранее;
5) учитель в виде тезисов записывает в «корзинке» все высказывания и идеи, включая ошибочные;
6) по мере освоения новой информации исправляются ошибки, вносятся необходимые дополнения.
В результате на доске появляются тезисы.
Учитель: В записях присутствует слово многогранник, что это значит?
Учащиеся дают определение многогранника: Многогранник это поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. (Определение выведено в glogster.)
Какой многогранник называется выпуклым?
Ученики: Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. (Определение выведено в glogster.)
Определите, какие из многогранников, изображенных на рисунке, являются выпуклыми? (Обращение к glogster.)
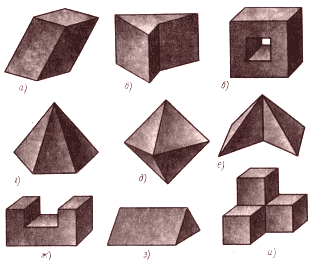
Учитель: Нами уже использовались словосочетания “правильные призмы” и “правильные пирамиды”. Оказывается, новая комбинация знакомых понятий образует совершенно новое с геометрической точки зрения понятие. Какие же выпуклые многогранники будем называть правильными? Послушайте внимательно определение.
3. Новый материал.
Выпуклый многогранник называется правильным, если все его грани– равные правильные многоугольниками и в каждой его вершине сходится одно и то же число ребер.

Работа с определением. При работе, постоянно привлекать учащихся к беседе, обсуждению.
Учитель: Убедимся что обе части определения необходимы. Уберём вторую часть определения. Выпуклый многогранник называется правильным если все его грани– равные правильные многоугольниками. Достаточно ли этого?Посмотрите на многогранник. (Демонстрируется модель многогранника, который получается из двух правильных тетраэдров, приклеенных друг к другу одной гранью). Оставляет ли он впечатление правильного многогранника? (Нет!). Посмотрим на его грани - правильные треугольники. Посчитаем число рёбер, сходящихся в каждой вершине. В некоторых вершинах сходятся три ребра, в некоторых – четыре. Вторая часть определения правильного выпуклого многогранника не выполняется и рассматриваемый многогранник действительно, не является правильным.
Попробуем убрать первую часть определения. Выпуклый многогранник называется правильным, если в каждой вершине многогранника сходится одно и то же число ребер.
Посмотрите на этот многогранник (демонстрируется модель параллелепипеда). Подсчитаем число ребер выходящих из каждой вершины – три ребра, грани не являются правильными многоугольниками. Первая часть определения не выполняется и этот многогранник не является правильным.
Таким образом, когда будете давать определение, помните об обеих его частях.
Выпуклый многогранник называется правильным, если все его грани– равные правильные многоугольниками и в каждой его вершине сходится одно и то же число ребер.
Учитель: Сколько углов что при вершине многогранного угла?
Ученики: Не менее трех плоских углов.
Учитель: Какова сумма плоских углов при вершине выпуклого многогранника?
Ученик: Меньше 3600.
Учитель: Давайте, посмотрим, какие правильные многоугольники могут быть гранями правильного многогранника и сколько правильных многогранников существует.
Исследуем этот вопрос. Результат оформим в виде таблицы (учитель на доске дети в рабочих листах).
| Форма граней | Сумма плоских углов при Вершине многогранника | Вывод |
 | 600 * 3 =1800 | |
 | 600 * 4 =2400 | |
 | 600 * 5 =3000 | |
 | 60*6=3600 | |
 | 900 * 3=2700 | |
 | 900 *4=3600 | |
 | 1080 * 3=3240 | |
 | 1080 *4=4320 | |
Объяснение материала происходит с одновременным показом иллюстраций в http://www.glogster.com/gala1348/-by-gala1348/g-6krl7e93b5cgn20ah2iuna0
Учитель: Всего существует пять видов правильных выпуклых многогранников. Их гранями являются правильные треугольники, правильные четырёхугольники (квадраты) и правильные пятиугольники. В соответствии с этим получается следующие правильные многогранники:
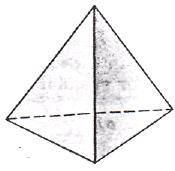
Правильный тетраэдр составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Сумма плоских углов при каждой вершине равна 180°.
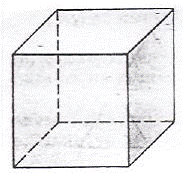
Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Сумма плоских углов при каждой вершине равна 270°. Частный случай параллелепипеда и призмы.
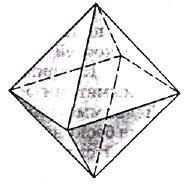
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Сумма плоских углов при каждой вершине – 240°.
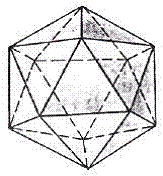
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Сумма плоских углов при каждой вершине равна 300°.
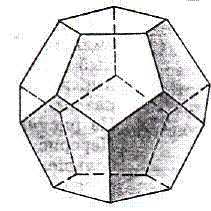
Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Сумма плоских углов при каждой вершине равна 324°.
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» – грань;
«тетра» – 4;
«гекса» – 6;
«окта» – 8;
«икоса» – 20;
«додека» – 12.
Форму правильных тел, по-видимому, подсказала древним грекам сама природа:
1) Кристаллы поваренной соли имеют форму куба;
2) Правильная форма алмаза – октаэдра;
3) Кристаллы пирита – додекаэдра.
Как отмечают историки, о существовании только пяти правильных многогранников знал еще Пифагор(VI век до н.э.), но первым удалось доказать это Евклиду (III век до н.э). Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени ;икосаэдр – как самый обтекаемый – воду; куб –самая устойчивая из фигур – землю, а октаэдр –воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.