Это была одна из первых попыток ввести в науку идею систематизации.

Вернутся к корзине и рассмотреть, что верно, что нет (можно редактировать в ходе обсуждения темы).

4. Исследовательская работа “Формула Эйлера”

Изучая любые многогранники, естественнее всего подсчитать, сколько у них граней, сколько рёбер и вершин. Подсчитаем и мы число указанных элементов правильных многогранников и занесём результаты в таблицу (раздаточный материал). Работаем в парах.

Правильный многогранник	Число граней	Число вершин	Число ребер	Г+В
Тетраэдр	4	4	6
Куб	6	8	12
Октаэдр	8	6	12
Додекаэдр	12	20	30
Икосаэдр	20	12	30

Учитель задает вопросы: Нет ли закономерности в возрастании чисел в каждом столбце? Какие закономерности можно заметить в первом и втором столбе?

Но можно рассмотреть сумму чисел в двух столбцах, хотя бы в столбцах “грани” и “вершины” (Г + В). Заполните четвертый столбец Г+В (число граней плюс число вершин).

Какой вывод можно сделать. Ученики пробуют его сформулировать .

Учитель подводит итог: “Сумма числа граней и вершин равна числу рёбер, увеличенному на 2 ”, т.е. Г + В = Р + 2. Запишите в рабочих листах. ( иллюстрация glogster)

Итак, мы вместе сделали открытие, мы “открыли”формулу, которая была подмечена уже Декартом в 1640г., а позднее вновь открыта Эйлером (1752), имя которого с тех пор она носит. Формула Эйлера верна для любых выпуклых многогранников. Запомните эту формулу.

Учитель: Большой интерес к формам правильных многогранников проявляли также скульпторы, архитекторы, художники. Их всех поражало совершенство, гармония многогранников. Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах.Сальвадор Дали на картине “Тайная вечеря” изобразил И.Христа со своими учениками на фоне огромного прозрачного додекаэдра. (иллюстрация glogster)

---

Правильные многогранники встречаются так же и в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр.
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

5. Итог урока:

Подходит к концу урок, подведём итоги. Давайте вернемся к началу урока, к игре верю, не верю. Попробуйте еще раз ответить на эти вопросы, поставив рядом + или -. Как правильно ответить на эти вопросы? На все ли вопросы Вы ответили верно? Остался ли вопрос на который мы не ответили? (Обсуждение с учащимися игры « Верю, не верю»). На вопрос «Существует модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.», ответа не прозвучало, на этот вопрос, предлагаю подготовить доклад.

Домашнее задание:

1) Склеить модели правильных многогранников на выбор;

2) Посмотреть glogster, ответить на загадки – карточки, посмотреть видео.

3) Решите задачи, используя план решения.

4) Подготовить доклад, по теме «Правильные многогранники», « Звездчатые многогранники».

Закончить урок фильмом о многообразии многогранников (при наличии времени).

Решите задачи используя план.

№1. Найдите высоту правильного тетраэдра с ребром 10 см.

Д 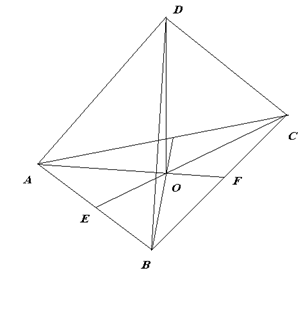ано: ABCД – правильный тетраэдр,
AВ = 10 см

Найти: высоту тетраэдра

Решение.

1) AF – медиана ΔABС, значит ВF = ______

2) Из ΔABF по теореме _______ найдем АF

AF²= AB² – BF² AF=________

3) О делит отрезок AF в отношении 2 :1, поэтому АО = _____________________

4) Из ΔADO по теореме Пифагора найдем DO

DO² = ____________ DO = ____________

Ответ: ______

№2. Решите задачу, используя план решения

Кристалл имеет форму октаэдра, состоящего из двух правильных пирамид с общим основанием, ребро основания пирамиды 6 см. Высота октаэдра 14 см. Найдите площадь боковой поверхности кристалла.


Решение.

1 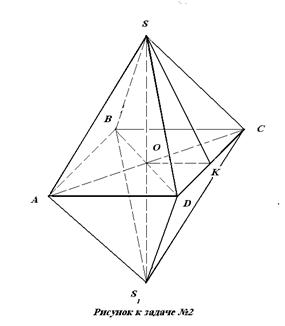) Sбок = 2 Sпир = p ∙ SK (где SK – апофема, p – полупериметр ABCD)

2) Находим ОК _________________________
______________________________________

---

3) Находим SO ________________________
______________________________________

4) Находим SK ________________________
______________________________________

5) Вычисляем Sбок ______________________
______________________________________

Ответ:

Карточка 1

. Отгадайте правильный многогранник:

1. 
   Грани этого многогранника связаны с “золотым сечением”.
   
2. 
   Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана, кристаллы которого имеют форму _________.
   
3. 
   Его удобно использовать для печати календарей.
   
4. 
   Правильный _____________ изображен на картине С. Дали “Тайная вечеря”.
   
5. 
   В школе Пифагора этот многогранник символизировал Вселенную
   

Карточка 2

. Отгадайте правильный многогранник:

1. 
   “Среди правильных тел самое первое, начало и родитель остальных – куб, а его, если позволительно сказать, супруга _______, ибо центры граней куба соответствуют вершинам _________” Иоганн Кеплер.
   
2. 
   При производстве алюминия пользуются алюминиево-калиевыми квасцами, монокристалл которых имеет форму ______________.
   
3. 
   Алмаз – самый твердый из минералов. Он может раскалываться в четырех направлениях, параллельно граням правильного ___________. Это свойство используют в ювелирном деле для придания камню необходимой формы перед огранкой.
   
4. 
   В школе Пифагора этот многогранник символизировал воздух.
   

Карточка 3

. Отгадайте правильный многогранник:

1. 
   Этот многогранник был игральной костью династии Птолемеев.
   
2. 
   Форму вируса гриппа часто сравнивают с формой этого многогранника.
   
3. 
   Его форму имеет кристалл бора. Бор использовался для создания полупроводников первого поколения.
   
4. 
   В школе Пифагора этот многогранник символизировал воду.
   
5. 
   В карточках последовательно зашифрованы додекаэдр, октаэдр и икосаэдр.
   

---

Смотрите также файлы

• Передаточные функции формирователей импульсов.pdf

• Великая Отечественная война дискуссионные вопросы истории.docx

• Детство и образование.docx

• Исследование операций и методы оптимизации Заданиевариант 2 Выполнена обучающимся группы о. Издтв 23. 1Б22.docx

• Открытый социальноэкономический колледж (ано по Открытый социальноэкономический колледж) Дисциплина статистика.docx