2.4. Параметрическая идентификация и проверка

адекватности математической модели
Используемые при изучении химико–технологических процессов математические модели содержат неизвестные постоянные или переменные величины (параметры), например, константы равновесной зависимости и скорости химической реакции, коэффициенты температуропроводности, молекулярной диффузии, массо- и теплоотдачи, продольной и радиальной диффузии и другие. Параметрическая идентификация математического описания предполагает отыскание по экспериментальным данным численных значений параметров, входящих в уравнения этого описания.

Для оценки неизвестных параметров в линейных моделях, описывающих объект моделирования, может быть использован метод наименьших квадратов. Сущность данного метода состоит в следующем. Для двух функций функционально связанных величин х и y известны n пар соответствующих значений (x_1;y₁), (x_2;y2),…, (x_n;y_n), требуется в наперед заданной формуле y=f(x,α₁, α₂,…, α_n.) определить m параметров α₁, α₂,…, α_m (m
Другим методом нахождения статистических оценок неизвестных параметров является метод максимального правдоподобия. Пусть имеем некоторые результаты наблюдений Х₁, Х₂, …, Х_n, которые являются непрерывными случайными величинами с одним и тем же распределением вероятностей f(x_n;θ), зависящим от одного неизвестного параметра θ. Суть метода максимального правдоподобия состоит в том, что в качестве оценок параметров выбираются те значения параметров, при которых данные результаты наблюдения “наиболее вероятны”. Для придания точного смысла принципу “наибольшей вероятности” вводят функцию правдоподобия:

f(x₁, x₂, …, x_n;θ) = p(x₁;θ), p(x₂;θ) … p(x_n;θ), (2.4.1)

где x₁, x₂, …, x_n – значения случайной величины; θ – значения параметра; f(x;θ) – плотность вероятности случайной величины Х_n.

Оценкой максимального правдоподобия параметра θ будет такое значение 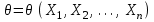, при котором функция правдоподобия достигает наибольшего возможного значения. Так как точка максимума для ln

---

f та же, что и для f, то для нахождения оценок максимального правдоподобия следует решать уравнение правдоподобия:

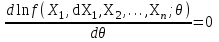. (2.4.2)

Оценка параметров по вероятности стремится к истинному значению, когда объем данных результатов наблюдений возрастает. Условия самостоятельности и регулярности обеспечивают асимптотическая нормальность и асимптотическая эффективность оценок параметров.

Рассмотрим несколько примеров нахождения параметров математических моделей. Ряд примеров проиллюстрируем с помощью системы Mathcad.

По известным экспериментальным данным найдем константу изотермы Генри в уравнении линейной равновесной зависимости:

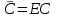, (2.4.3)

где С – равновесная концентрация раствора, 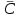– количество поглощенного вещества адсорбентом, Е – константа Генри.

На рис. 2.1 показан пример проведения линейной регрессии с помощью встроенной в систему Mathcad функции slope(VX,VY)



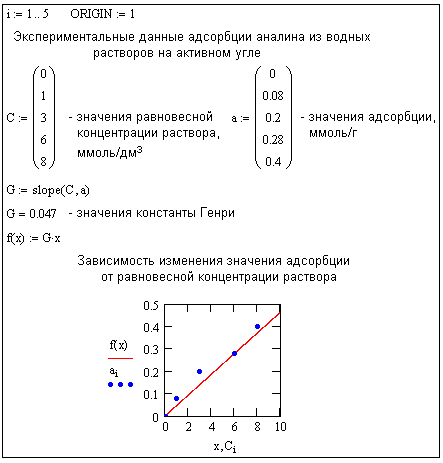
Рис. 2.1. Пример вычисления константы Генри
В случае, когда функционально связанные величины описываются нелинейным уравнением, равновесная зависимость предварительно преобразовывается заменой переменных к линейной. В качестве примера рассмотрим уравнение нелинейной изотермы Фрейндлиха:

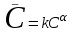, (2.4.4)

где k и α – константы изотермы Фрейндлиха.

Логарифмируя последнее равенство, получаем

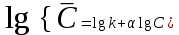. (2.4.5)

Полагая ,

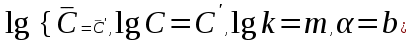имеем

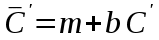. (2.4.6)

Графиком линейного уравнения (2.4.6) служит прямая, тангенс угла наклона которой будет равен b, а точка пересечения прямой с осью ординат будет соответствовать параметру m.

Входящий в исследуемую математическую модель неизвестный параметр может быть найден из расчетов по известной, хорошо отработанной математической модели. Например, константа скорости химической реакции для реакции первого порядка находится по уравнению:

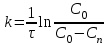, (2.4.7)

В случае реакции второго порядка имеем:

---

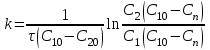, (2.4.8)

где С₀, С₁₀, С₂₀ – начальные концентрации реагирующих веществ, кмоль/м³; С_п – концентрация образующегося продукта, кмоль/м³.

Для определения коэффициента температуро–проводности в частице твердой фазы может быть использован метод нестационарного режима [1]. Полагают, что частица имеет правильную геометрическую форму. Значение коэффициента температуропроводности в течение всего процесса нагрева частицы является величиной постоянной. На основе использования известных аналитических решений задач о поглощении теплоты частицей подбирается наилучшее значение коэффициента температуропроводности из условия минимума среднеквадратичного отклонения, рассчитываемого по формуле:

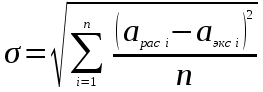, (2.4.9)

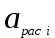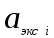где и – расчетные и экспериментальные данные средней температуры частицы; n – число точек на кривых изменения температуры частицы в зависимости от времени.

Данный метод может быть также применен для определения коэффициента молекулярной диффузии в кинетических моделях адсорбции.

При изучении динамики концентрационных полей внутри частицы твердой фазы с помощью моделей с переменным коэффициентом диффузии может быть применен зональный метод [2]. В соответствии с этим методом величина коэффициента диффузии для i–го участка кинетической кривой находится по формуле:

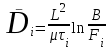, (2.4.10)

где L – определяющий размер (половина толщины пластины, радиус цилиндра или шара); 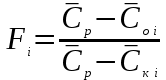– средняя относительныя концентрация, 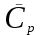– расчетные значения средней концентрации компонента в частице, 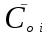– начальная средняя концентрация компонента в частице,  и В – коэффициенты, зависящие от формы частицы: для неограниченной пластины: μ=π/2, B=2/μ²; для неограниченного цилиндра: μ=2,4048, B=4/μ²; для шара: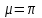

---

, B=6/μ².

На рис. 2.2 приведен пример определения коэффициента молекулярной диффузии на небольшом временном интервале в кинетической модели десорбции в системе Mathcad с помощью функции genfit.

Скорость протекания теплообменных процессов в неравновесных бинарных или многокомпонентных системах характеризуется коэффициентом теплопередачи К. Например, значение К для теплообмена между двумя средами, разделенными стенкой, рассчитывается по уравнению:

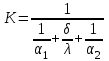, (2.4.11)

где α₁ и α₂ – коэффициенты теплоотдачи со стороны “горячего” и “холодного” теплоносителей; δ – толщина стенки; λ – коэффициент теплопроводности стенки.


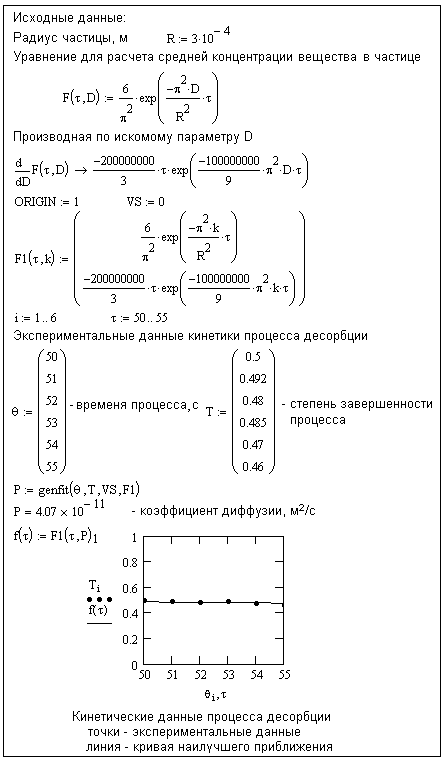
Рис. 2.2. Пример расчета коэффициента диффузии

Коэффициенты теплоотдачи находятся из критериальных соотношений вида:

Nu=f(Re, Pr, Gr, Г), (2.4.12)

где 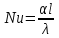– критерий Нуссельта; 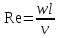– критерий Рейнольдса; 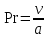– критерий Прандтля; 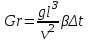– критерий Грасгофа; Г – симплекс геометрического подобия; а – коэффициент температуропроводности; g – ускорение свободного падения; w – средняя скорость движения среды; β – коэффициент термического расширения.

В случае естественной циркуляции кинетика теплопередачи описывается уравнением:

Nu=f(Pr, Gr, Г). (2.4.13)

Для конкретных условий проведения процесса критериальные уравнения (2.4.12) и (2.4.13) в явном виде можно найти в литературе [3,4].

Одним из основных кинетических параметров массообменного процесса является коэффициент массопередачи. При его расчете учитывают перенос вещества от границы раздела фаз внутрь фазы и перенос вещества через поверхность раздела фаз. Напрмер, в системе газ–жидкость коэффициент массопередачи, отнесенный к газовой фазе, рассчитывается по уравнению:

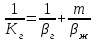, (2.4.14)

где β_г и β_ж – коэффициенты массоотдачи в газовой и жидкой фазе, соответственно; m – константа фазового равновесия.

Коэффициент массоотдачи

---

определяется обычно из критериальной зависимости, которая в общем виде можетбыть записана так:

Nu’=f(Pr’, Re, Fr, Г), (2.4.15)

где 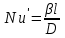– диффузионный критерий Нуссельта, 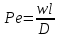– диффузионный критерий Пекле.

Если определение истинной поверхности контакта фаз затруднительно, то в расчетах используют объемные коэффициенты массопередачи

К_{г v} =К_га, К_{ж v} =К_жа (2.4.16)

и массоотдачи

β_{г v} =β_га, β_{ж v} =β_жа, (2.4.17)

где а – поверхность контакта фаз, приходящаяся на 1 м³ объема газожидкостной системы.

Для расчета коэффициентов массоотдачи, как правило, используют критериальные уравнения, полученные методом теории подобия или на основе аналогии между процессами переноса массы и теплоты. Данные уравнения можно найти в литературе [3,4].

Опытные критериальные зависимости также обычно используются для нахождения коэффициентов продольного и поперечного перемешивания фаз в диффузионных моделях структуры потоков в аппарате.

Поскольку параметры процесса, используемые для расчетов, а в общем случае и само математическое описание лишь с определенной точностью отражают реальные закономерности химико–технологического процесса, то используемые математические модели необходимо проверять на адекватность путем сравнения теоретических и экспериментальных результатов с привлечением методов статиcтической проверки гипотез.

Оценку соответствия теоретических выводов экспериментальным данным проводят с помощью критерия Фишера:

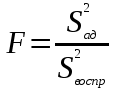, (2.4.18)

где 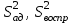– соответственно дисперсия адекватности и дисперсия воспроизводимости, определяемые по формулам:

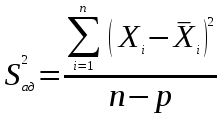, (2.4.19)

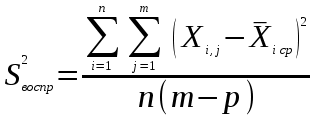, (2.4.20)

где n – объем выборки; m – количество параллельных опытов; 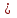– экспериментальные и расчетные данные, соответственно; X

---

Смотрите также файлы

• Малые тела Солнечной системы астероиды, карликовые планеты, кометы.docx

• Лабораторная эконометрика.docx

• Электроэнергетика и электротехника.docx

• Социально культурный проект Школа искусств Актуальность. Какую проблему решает проект Отсутствие условий и площадок для реализации культурного и художественного .pptx

• Задание на курсовую работу по мдк 01. 01. Разработка нефтяных и газовых месторождений.docx