Файл: 2 Параметрическая идентификация и проверка адекватности математической модели.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
i ср – среднее значение из результатов параллельных опытов, 
; (n - p) – число степеней свободы для дисперсии 
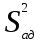; n (m - р) – число степеней свободы для дисперсии 
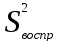; p – число значимых коэффициентов.
В случае проведения отдельной серии из m повторных экспериментов число степеней свободы дисперсии воспроизводимости равно m-1.
Отношение выборочных дисперси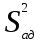й и 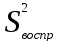(2.4.18) сравнивается с табличным значением критерия Фишера Fтабл для заданного уровня значимости. Если F Fтабл, то принимается, что рассматриваемая модель адекватно описывает реальный процесс. В противном случае модель отвергается.
На рис. 2.3 приведен пример установления адекватности расчетной кривой распределения средних размеров частиц экспериментальным данным по критерию Фишера. В табл. 2.1 приведены экспериментальные данные ситового анализа.
Таблица 2.1
Гранулометрический состав сыпучего материала
Для каждой фракции находили средний размер частиц материала по формуле:
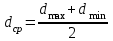. (2.4.21)
Соответствующее табличное значение критерия Фишера для степеней свободы 9 и 3 и уровня значимости α=0,01 составляет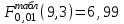
. Так как 
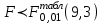, то расчетная кривая распределения адекватна эксперименту.
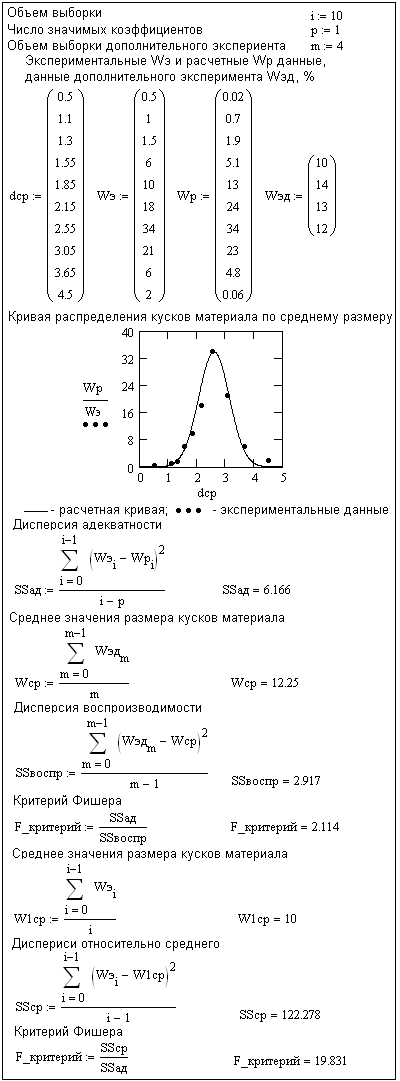
Рис. 2.3. Пример установления адекватности математической
модели эксперименту по критерию Фишера
Табулированное значение критерия Фишера при уровне значимости α=0,01 и для степеней свободы 9 и 9 равно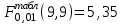
, и так как F>Fтабл, то расчетную кривую распределения использовать целесообразно.
Если дисперсия σ2 неизвестна, то для проверки гипотезы а=а0 можно воспользоваться критерием Стьюдента:
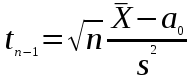, (2.4.22)
где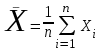
; 
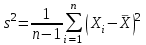; а0 – математическое ожидание.
При условии, что гипотеза а=а0 справедлива, статистика tn-1 имеет распределение Стьюдента с n-1 степенями свободы. Если при заданном уровне значимости α справедливо равенство
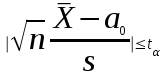, (2.4.23)
то гипотеза принимается.
Для проверки гипотезы о неизвестном значении σ2 используется критерий Пирсона. Всю область значений случайных величин Х1, . . ., Хn разделяют на r интервалов. Берут выборку, попавшую на интервал ri, и обозначают за ni число элементов выборки. Проверка гипотезы соответствия частоты появления некоторого события вероятностям pi по всем интервалам основана на статистике
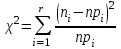. (2.4.24)
Если гипотеза справедлива, то величина будет иметь хи-квадрат распределение со степенью свободы r-1. Число степеней свободы снизится до r-1-k, если по результатам наблюдений определяется k параметров распределения.
Если χ2 больше табличного значения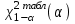
, то гипотеза согласия отвергается.
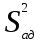; (n - p) – число степеней свободы для дисперсии ; n (m - р) – число степеней свободы для дисперсии 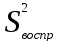; p – число значимых коэффициентов.В случае проведения отдельной серии из m повторных экспериментов число степеней свободы дисперсии воспроизводимости равно m-1.
Отношение выборочных дисперси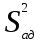й
и 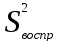(2.4.18) сравнивается с табличным значением критерия Фишера Fтабл для заданного уровня значимости. Если F Fтабл, то принимается, что рассматриваемая модель адекватно описывает реальный процесс. В противном случае модель отвергается.На рис. 2.3 приведен пример установления адекватности расчетной кривой распределения средних размеров частиц экспериментальным данным по критерию Фишера. В табл. 2.1 приведены экспериментальные данные ситового анализа.
Таблица 2.1
Гранулометрический состав сыпучего материала
| Фракция | 0-1 | 1-1,2 | 1,2-1,4 | 1,4-1,7 | 1,7-2 | 2-2,3 | 2,3-2,8 | 2,8-3,3 | 3,4-4 | 4-5 |
| W, % | 0,5 | 1 | 1,5 | 6 | 10 | 18 | 34 | 21 | 6 | 2 |
Для каждой фракции находили средний размер частиц материала по формуле:
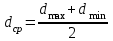. (2.4.21)Соответствующее табличное значение критерия Фишера для степеней свободы 9 и 3 и уровня значимости α=0,01 составляет
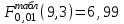. Так как 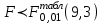, то расчетная кривая распределения адекватна эксперименту.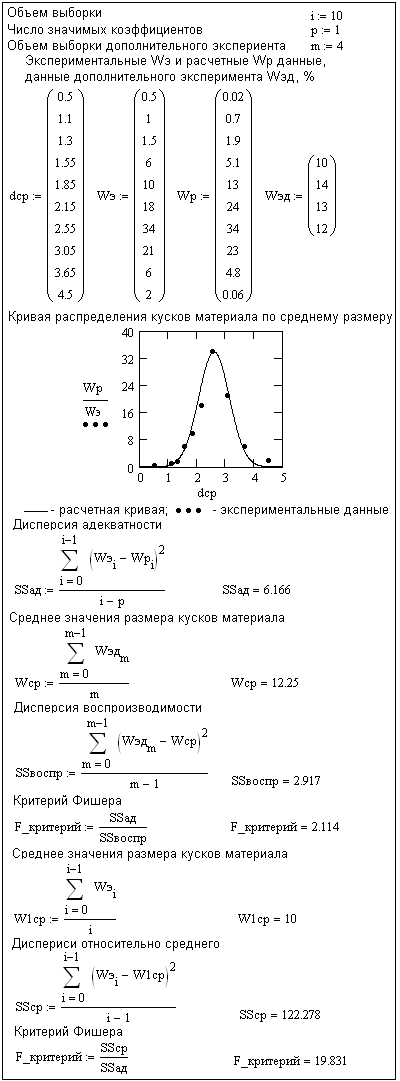 Рис. 2.3. Пример установления адекватности математической
модели эксперименту по критерию Фишера
Табулированное значение критерия Фишера при уровне значимости α=0,01 и для степеней свободы 9 и 9 равно
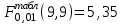, и так как F>Fтабл, то расчетную кривую распределения использовать целесообразно.Если дисперсия σ2 неизвестна, то для проверки гипотезы а=а0 можно воспользоваться критерием Стьюдента:
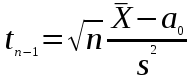, (2.4.22)где
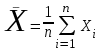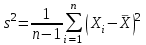; ; а0 – математическое ожидание.При условии, что гипотеза а=а0 справедлива, статистика tn-1 имеет распределение Стьюдента с n-1 степенями свободы. Если при заданном уровне значимости α справедливо равенство
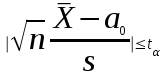, (2.4.23)то гипотеза принимается.
Для проверки гипотезы о неизвестном значении σ2 используется критерий Пирсона. Всю область значений случайных величин Х1, . . ., Хn разделяют на r интервалов. Берут выборку, попавшую на интервал ri, и обозначают за ni число элементов выборки. Проверка гипотезы соответствия частоты появления некоторого события вероятностям pi по всем интервалам основана на статистике
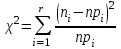. (2.4.24)Если гипотеза справедлива, то величина будет иметь хи-квадрат распределение со степенью свободы r-1. Число степеней свободы снизится до r-1-k, если по результатам наблюдений определяется k параметров распределения.
Если χ2 больше табличного значения
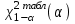, то гипотеза согласия отвергается.