Файл: Исследование цель исследования изучить направления дальнейшего развития.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 134
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- девальвация;
- валютные ограничения;
- финансовая и денежно-кредитная политика;
- специальные меры воздействия на платежный баланс в ходе формирования его основных статей: торгового баланса, «невидимы» операций (ограничение нормы вывоза валюты туристами данной страны, регулирование миграции рабочей силы), движения капиталов.
При активном платежном балансе регулирование направлено на устранение чрезмерно активного сальдо. Активное сальдо используется для погашения внешней задолженности страны, предоставления кредитов иностранным государствам, увеличения золотовалютных запасов.
1.2 Показатели динамики торгового баланса
Статистическое изучение динамики показателей таможенной статистики основывается на обработке рядов динамики, включая анализ изменения их уровней ряда, выявление основной тенденции и закономерностей развития.
Временной ряд представляет собой последовательность измерений в последовательные периоды времени. Анализ временных рядов основывается на предположении, что последовательные значения в наборе данных наблюдаются через равные промежутки времени.
В зависимости от способа выражений уровней (в виде абсолютных, относительных и средних величин) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.
В зависимости от того, выражают уровни ряда состояние явлений на определенные моменты времени (на начало месяца, года) или его величину за определенные интервалы времени (за месяц, квартал) различают соответственно моментные и интервальные ряды.
Примером моментного временного ряда является ряд динамики, показывающий число принятых грузовых таможенных деклараций на 1 июня каждого года за несколько лет.
Примером интервального ряда динамики может быть ряд, содержащий ежемесячные (ежедневные, ежеквартальные, ежегодные) данные об экспорте (импорте) Российской Федерации5.
Изучение социально-экономических процессов на основе анализа временных рядов включает следующие этапы:
1) постановка задачи и подбор исходной информации;
2) предварительный анализ исходных временных рядов и формирование модели (моделей) анализа и прогнозирования;
3) оценка параметров и качества модели (моделей);
4) построение прогноза, комментарий полученного прогноза.
На основании имеющихся абсолютных значений основных показателей рассчитываются характеристики динамических рядов. Характеристики динамических рядов – это показатели, которые характеризуют изменения явления во времени.
К статистическим характеристикам динамического ряда относятся:
1) приросты (базисные, цепные, средний);
2) темпы роста (базисные, цепные, средний);
3) темпы прироста (базисные, цепные, средний)6.
Абсолютный прирост (
Для первого случая справедливо выражение:
где
Для второго случая используется формула:
где
Между цепным и базисным абсолютным приростом существует взаимосвязь – сумма цепных дает соответствующий базисный абсолютный прирост.
За весь период, описываемый рядом, абсолютный прирост выразится как разность между последним и первым уровнем ряда:
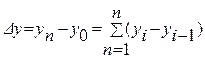 , (3)
, (3)Абсолютный прирост может быть как положительным, так и отрицательным и обязательно имеет единицы измерения и размерность.
Коэффициент (темп) роста (Тр, Кр) – это соотношение последующего уровня ряда к предыдущему (цепной) или постоянному, принятому за базу сравнения (базисный):
Цепные коэффициенты (темпы) роста рассчитываются по формулам:
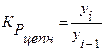 , (4)
, (4)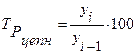 , (5)
, (5)где
2) базисные коэффициенты (темпы) роста рассчитываются по формуле:
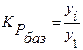 , (6)
, (6)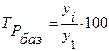 , (7)
, (7)где
Цепной способ характеризует последовательное изменение, а базисный способ – изменение нарастающим итогом.
Между цепными и базисными коэффициентами роста существует взаимосвязь – произведение цепных коэффициентов роста дает соответствующий базисный коэффициент роста.
Темп прироста показывает, на сколько процентов изменяется данный уровень по сравнению с предыдущим уровнем ряда при цепном способе и с начальным уровнем ряда при базисном способе.
Для первого случая справедливо выражение:
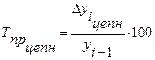 , (8)
, (8)где
Во втором случае используется формула:
 , (9)
, (9)где
Темп прироста обычно выражается в процентах и показывает, на сколько процентов увеличился или уменьшился текущий уровень по сравнению с предыдущим (базисным).
Темп и коэффициент прироста также можно определить исходя из темпа и коэффициента роста:
Так как показатели в течение рассматриваемого периода времени изменяются, изменяются и характеристики ряда. Поэтому, чтобы получить общее представление об изменении данных показателей, следует найти обобщающие характеристики, то есть средние величины.
Средний абсолютный прирост (
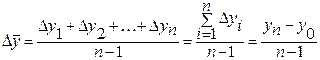 , (14)
, (14)где
n-1 – количество изменений за данный период;
Средний темп роста (
Средний темп роста определяется всегда по средней геометрической. Средний темп роста можно определить исходя из цепных коэффициентов (темпов) роста:
или абсолютных уровней ряда (базисного темпа роста):
, (16)
где
n-1 – количество изменений за данный период.
Средний темп роста обычно выражается в коэффициентах, но может быть и в процентах.
Средний темп прироста (
где
Средний темп прироста показывает, на сколько процентов изменился уровень ряда в среднем за данный период.
Средний темп прироста выражается в коэффициентах (коэффициент прироста) или в процентах.
Вычисление данных показателей является первым этапом анализа динамических рядов и позволяет выявить скорость и интенсивность развития явления, представленного данным рядом7.