Файл: Исследование взаимосвязи данных показателей с помощью диаграммы рассеяния и коэффициента корреляции.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
целом статистически значима.
Значимость оценок параметров проверяется при помощи неравенства:

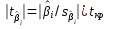
Воспользуемся значениями t-статистики полученными при проведении регрессионного анализа

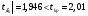 — оценка
— оценка 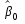 статистически не значима при уровне значимости
статистически не значима при уровне значимости  ,
,
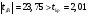 — оценка
— оценка 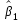 статистически значима при уровне значимости
статистически значима при уровне значимости  .
.
Таким образом, регрессоры, включённые в спецификацию модели статистически значимо влияют на эндогенную переменную.
Промежуточные вычисления для получения средней относительной ошибки аппроксимации.
Воспользовавшись данными из табл., получим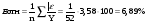 . Точность модели достаточно высокая.
. Точность модели достаточно высокая.
В целом качество модели признается высоким.
Строим график остатков
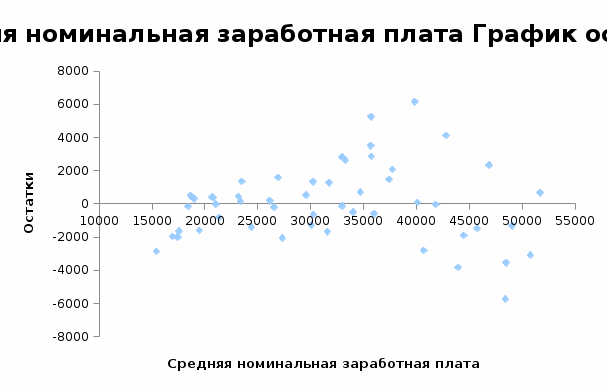
На рис. нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы
В соответствии с алгоритмом теста Дарбина-Уотсона по оцененной модели вычислим оценки эндогенной переменной
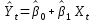 ,
, 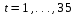 ,
,
и остатки
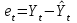 ,
, 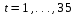 ,
,
по которым по формуле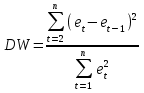 вычислим значение статистики теста. Вычисление показателей удобно выполнять в виде таблицы
вычислим значение статистики теста. Вычисление показателей удобно выполнять в виде таблицы
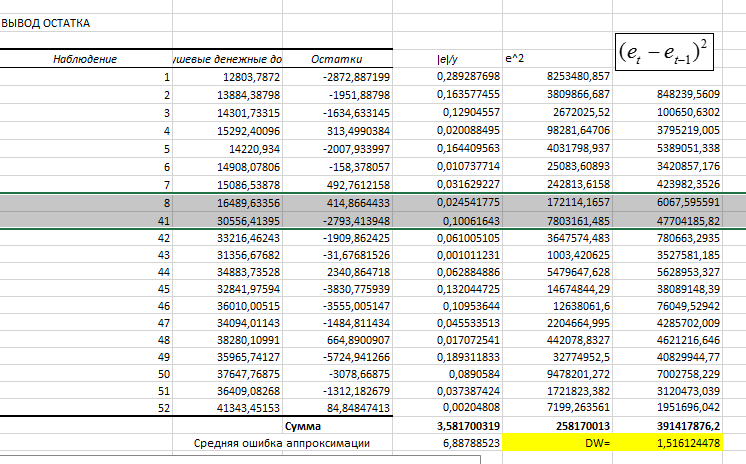
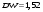
Нижняя и верхняя границы критического значения статистики,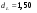 и
и 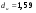 , определённые по таблице Дарбина-Уотсона для
, определённые по таблице Дарбина-Уотсона для  ,
, 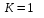 (число регрессоров модели),
(число регрессоров модели), 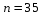 (число наблюдений) делят интервал возможных значений на пять частей
(число наблюдений) делят интервал возможных значений на пять частей
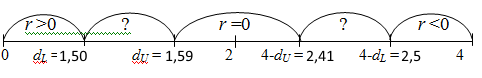
Вычисленное значение статистики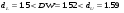 попадает в интервал неопределенности. Нельзя сделать вывод на основании данного критерия
попадает в интервал неопределенности. Нельзя сделать вывод на основании данного критерия
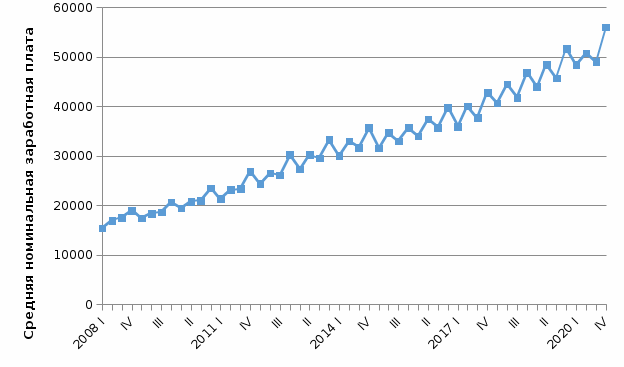
График показывает наличие тренда и сезонной компоненты с периодичностью 4 квартала. Поэтому для учета сезонности понадобится 3 фиктивные переменные.
Запишем спецификацию регрессионной модели с фиктивными переменными сдвига, учитывающими сезонные колебания
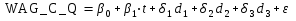 ,
,
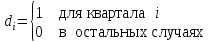 ,
, 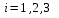 .
.
Параметры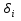 ,
, 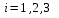 показывают средние квартальные отклонения средней номинальной заработной платы по отношению к четвертому (базовому) кварталу. Построим полученную модель с использованием сервиса Анализ данных – Регрессия
показывают средние квартальные отклонения средней номинальной заработной платы по отношению к четвертому (базовому) кварталу. Построим полученную модель с использованием сервиса Анализ данных – Регрессия
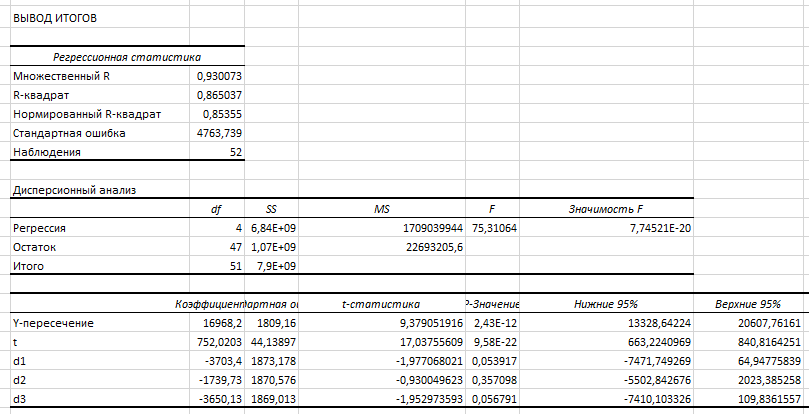 Оцененная модель имеет вид:
Оцененная модель имеет вид:
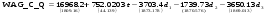 ,
,
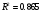 ,
, 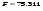 ,
, 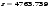 .
.
Влияние первых трех кварталов на эндогенную переменную статистически не значимо отличается от влияния на неё базового (четвертого) квартала для уровня значимости
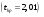
Поскольку оцененная модель — множественная регрессионная, для неё необходимо вычислить скорректированный коэффициент детерминации по формуле:
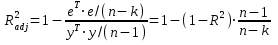 ,
,
Также он приведен в первой таблице Регрессионного анализа
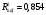
Критическое значение F – статистики для параметров: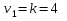 ,
,
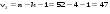
и уровня значимости равно
равно 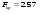 , таким образом
, таким образом 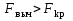 , и, следовательно, оцененная регрессия в целом статистически значима.
, и, следовательно, оцененная регрессия в целом статистически значима.
По оцененной модели построим прогноз на ближайший квартал, т.е. на 1 квартал 2021 года:
Подставляем значения
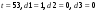 Получим:
Получим:
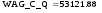
Подставив прогнозные значения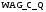
 в модель (1), получим точечный прогноз
в модель (1), получим точечный прогноз  :
:
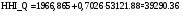
Построим интервальную оценку значения эндогенной переменной на интервале прогнозирования для момента ,
,


 нижняя граница интервала прогнозирования;
нижняя граница интервала прогнозирования;
 — верхняя граница интервала прогнозирования;
— верхняя граница интервала прогнозирования;
 — табличное значение критерия Стьюдента.
— табличное значение критерия Стьюдента.
 – ошибка прогноза, вычисляется по формуле:
– ошибка прогноза, вычисляется по формуле:

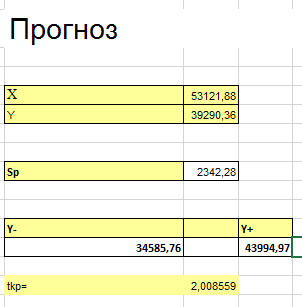
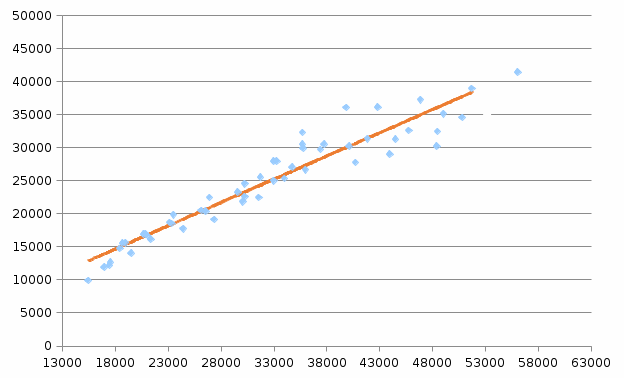
Отразим результаты на графике
Значимость оценок параметров проверяется при помощи неравенства:
Воспользуемся значениями t-статистики полученными при проведении регрессионного анализа

Таким образом, регрессоры, включённые в спецификацию модели статистически значимо влияют на эндогенную переменную.
Промежуточные вычисления для получения средней относительной ошибки аппроксимации.
| Наблюдение | Предсказанное Среднедушевые денежные доходы населения (HHI_Q) | Остатки | |e|/y |
| 1 | 12803,7872 | -2872,887199 | 0,289287698 |
| 2 | 13884,38798 | -1951,88798 | 0,163577455 |
| 3 | 14301,73315 | -1634,633145 | 0,12904557 |
| 4 | 15292,40096 | 313,4990384 | 0,020088495 |
| 5 | 14220,934 | -2007,933997 | 0,164409563 |
| 6 | 14908,07806 | -158,378057 | 0,010737714 |
| 7 | 15086,53878 | 492,7612158 | 0,031629227 |
| 8 | 16489,63356 | 414,8664433 | 0,024541775 |
| 9 | 15657,05103 | -1591,95103 | 0,11318448 |
| 10 | 16587,29514 | 380,6048642 | 0,022430876 |
| 11 | 16743,27262 | -12,67262178 | 0,000757452 |
| 12 | 18471,67179 | 1361,628209 | 0,068653639 |
| 13 | 16970,21284 | -823,8128379 | 0,051021456 |
| 14 | 18234,89516 | 455,1048434 | 0,024350179 |
| 15 | 18374,01021 | 175,3897883 | 0,009455281 |
| 16 | 20870,35259 | 1585,647411 | 0,070611303 |
| 17 | 19115,25457 | -1404,654571 | 0,079311518 |
| 18 | 20618,82133 | -201,2213275 | 0,009855288 |
| 19 | 20323,72879 | 188,5712135 | 0,00919308 |
| 20 | 23208,60968 | 1326,390324 | 0,05406115 |
| 21 | 21175,28155 | -2054,281548 | 0,107435885 |
| 22 | 23217,04089 | -626,0408913 | 0,02771196 |
| 23 | 22748,40583 | 532,2941679 | 0,022864182 |
| 24 | 25341,70719 | 2644,492813 | 0,094492743 |
| 25 | 23084,95185 | -1284,951849 | 0,058942745 |
| 26 | 25126,71119 | -136,3111927 | 0,005454542 |
| 27 | 24260,4038 | 1268,296196 | 0,04968119 |
| 28 | 27039,1919 | 3493,708101 | 0,114424378 |
| 29 | 24145,17719 | -1688,077193 | 0,075168975 |
| 30 | 26349,23743 | 710,0625658 | 0,026240981 |
| 31 | 25140,76322 | 2823,836782 | 0,10097898 |
| 32 | 27044,11011 | 5240,889892 | 0,162332039 |
| 33 | 25855,30873 | -491,3087286 | 0,019370317 |
| 34 | 28246,96351 | 1476,136486 | 0,049662938 |
| 35 | 27080,64538 | 2864,854625 | 0,095668953 |
| 36 | 29947,25863 | 6152,541369 | 0,170431453 |
| 37 | 27248,56708 | -602,3670831 | 0,022606116 |
| 38 | 30143,28439 | 90,71560948 | 0,00300045 |
| 39 | 28471,09332 | 2068,406675 | 0,067728898 |
| 40 | 32036,09226 | 4113,407739 | 0,113788787 |
| 41 | 30556,41395 | -2793,413948 | 0,10061643 |
| 42 | 33216,46243 | -1909,862425 | 0,061005105 |
| 43 | 31356,67682 | -31,67681526 | 0,001011231 |
| 44 | 34883,73528 | 2340,864718 | 0,062884886 |
| 45 | 32841,97594 | -3830,775939 | 0,132044725 |
| 46 | 36010,00515 | -3555,005147 | 0,10953644 |
| 47 | 34094,01143 | -1484,811434 | 0,045533513 |
| 48 | 38280,10991 | 664,8900907 | 0,017072541 |
| 49 | 35965,74127 | -5724,941266 | 0,189311833 |
| 50 | 37647,76875 | -3078,66875 | 0,0890584 |
| 51 | 36409,08268 | -1312,182679 | 0,037387424 |
| 52 | 41343,45153 | 84,84847413 | 0,00204808 |
| Сумма | 3,581700319 | ||
| Средняя ошибка аппроксимации | 6,88788523 | ||
Воспользовавшись данными из табл., получим
В целом качество модели признается высоким.
Строим график остатков

На рис. нет особых различий между ошибками, соответствующими разным значениям Xi. Следовательно, вариации ошибок при разных значениях Хi приблизительно одинаковы
В соответствии с алгоритмом теста Дарбина-Уотсона по оцененной модели вычислим оценки эндогенной переменной
и остатки
по которым по формуле
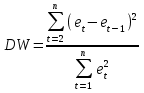 вычислим значение статистики теста. Вычисление показателей удобно выполнять в виде таблицы
вычислим значение статистики теста. Вычисление показателей удобно выполнять в виде таблицы 
Нижняя и верхняя границы критического значения статистики,
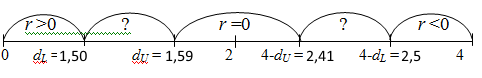
Вычисленное значение статистики

График показывает наличие тренда и сезонной компоненты с периодичностью 4 квартала. Поэтому для учета сезонности понадобится 3 фиктивные переменные.
Запишем спецификацию регрессионной модели с фиктивными переменными сдвига, учитывающими сезонные колебания
Параметры
 Оцененная модель имеет вид:
Оцененная модель имеет вид:Влияние первых трех кварталов на эндогенную переменную статистически не значимо отличается от влияния на неё базового (четвертого) квартала для уровня значимости
Поскольку оцененная модель — множественная регрессионная, для неё необходимо вычислить скорректированный коэффициент детерминации по формуле:
Также он приведен в первой таблице Регрессионного анализа
Критическое значение F – статистики для параметров:
и уровня значимости
По оцененной модели построим прогноз на ближайший квартал, т.е. на 1 квартал 2021 года:
Подставляем значения
Подставив прогнозные значения
Построим интервальную оценку значения эндогенной переменной на интервале прогнозирования для момента


Отразим результаты на графике
