Файл: The Microphone Handbook..pdf

THE MICROPHONE BOOK

18

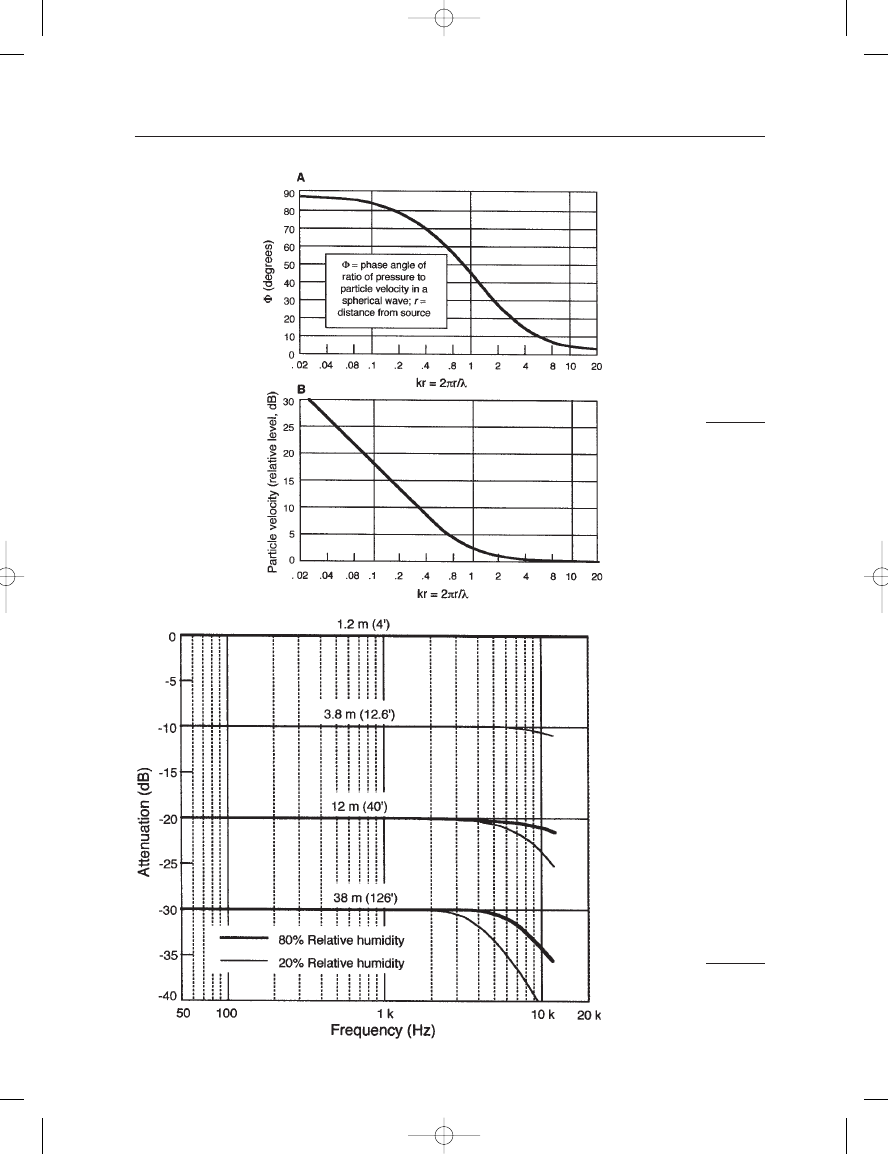
FIGURE 2–10

Spherical sound waves:
phase angle between
pressure and particle
velocity in a spherical 
wave at low frequencies; r
is the observation distance
and 

 is the wavelength of

the signal (A); increase in
pressure gradient in a
spherical wave at low
frequencies (B).

FIGURE 2–11

Effects of both inverse
square relationships and
HF air losses (20% and
80% RH).

Earg_02.qxd  14/9/04  2:35 PM  Page 18

2: Basic Sound Transmission and Operational Forces on Microphones

19

DIFFRACTION EFFECTS AT SHORT WAVELENGTHS;

DIRECTIVITY INDEX (DI)

Microphones are normally fairly small so that they will have minimal effect
on the sound field they are sampling. There is a limit, however, and it is dif-
ficult to manufacture studio quality microphones smaller than about 12 mm
(0.5 in) in diameter. As microphones operate at higher frequencies, there are
bound to be certain aberrations in directional response as the dimensions of
the microphone case become a significant portion of the sound wavelength.
Diffraction refers to the bending of sound waves as they encounter objects
whose dimensions are a significant portion of a wavelength.

Many measurements of off-axis microphone response have been

made over the years, and even more theoretical graphs have been devel-
oped. We will now present some of these.

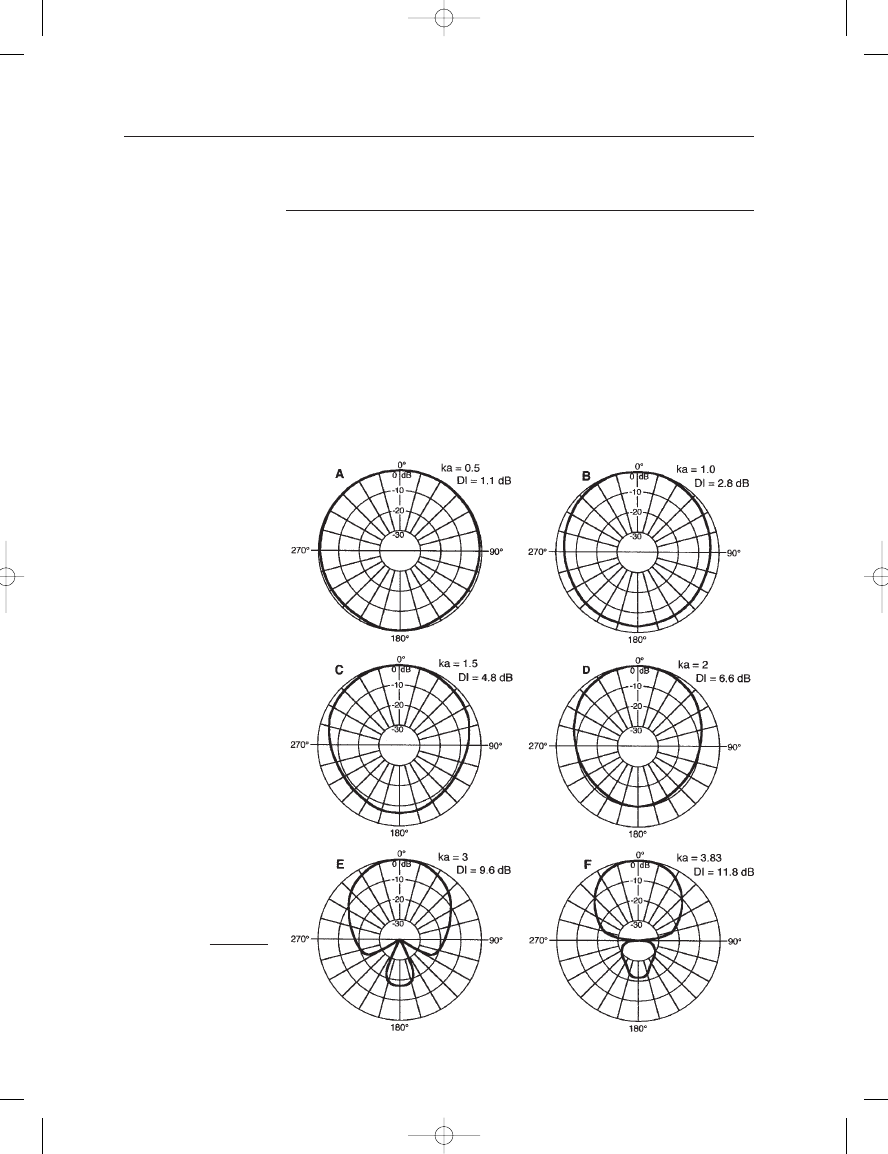
FIGURE 2–12

Theoretical polar 
response for a microphone
mounted at the end of a
tube. (Data presentation
after Beranek, 1954.)

Earg_02.qxd  14/9/04  2:35 PM  Page 19

THE MICROPHONE BOOK

20

Figure 2–12 shows polar response diagrams for a circular diaphragm

at the end of a long tube, a condition that describes many microphones. In
the diagrams, ka

 2a/, where a is the radius of the diaphragm. Thus,

ka represents the diaphragm circumference divided by wavelength. DI
stands for directivity index; it is a value, expressed in decibels, indicating
the ratio of on-axis pickup relative to the total pickup integrated over all
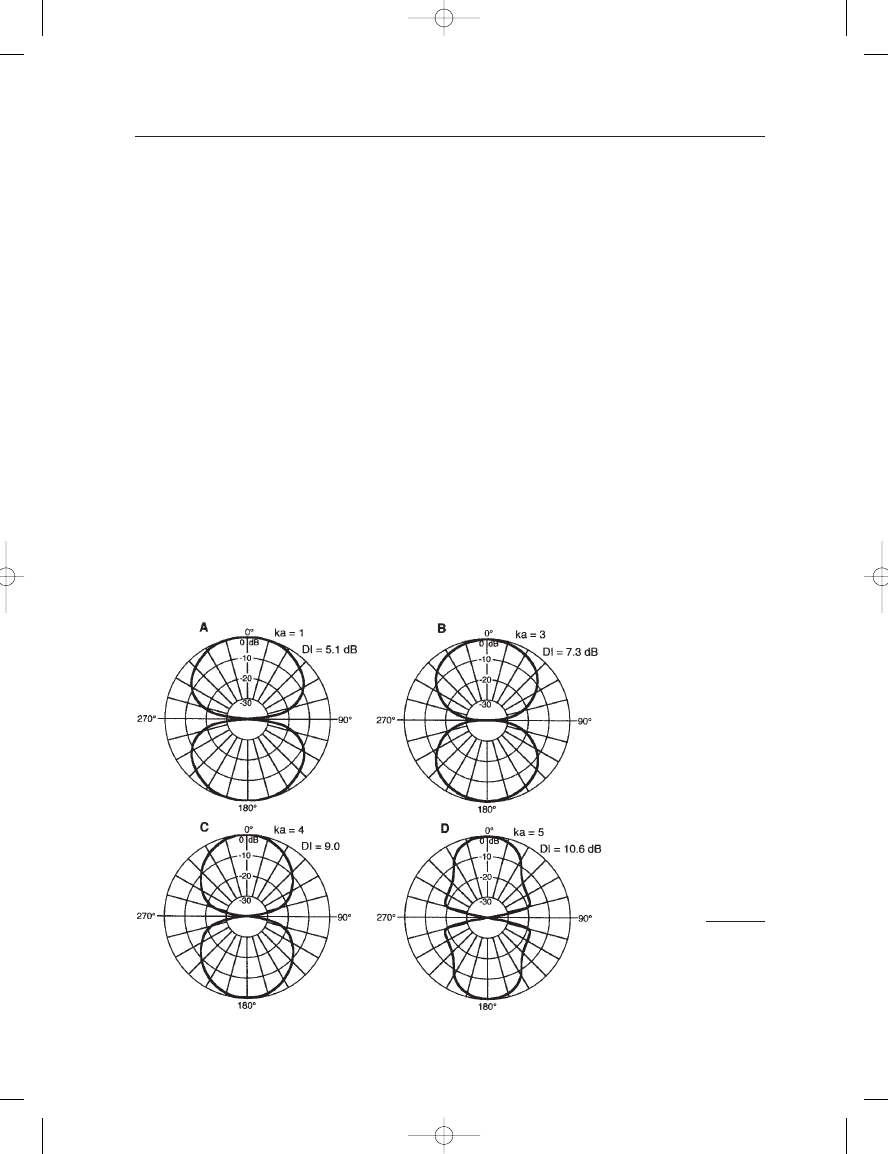
directions. Figure 2–13 shows the same set of measurements for a micro-
phone which is effectively open to the air equally on both sides. It repre-
sents the action a ribbon microphone, with its characteristic “figure-eight”
angular response.

Figure 2–14 shows families of on- and off-axis frequency response

curves for microphones mounted on the indicated surfaces of a cylinder
and a sphere. Normally, a limit for the HF response of a microphone
would be a diameter/

 ratio of about one.

In addition to diffraction effects, there are related response aberra-

tions due to the angle at which sound impinges on the microphone’s
diaphragm. Figure 2–15A shows a plane wave impinging at an off-axis
oblique angle on a microphone diaphragm subtended diameter which is
one-fourth of the sound wavelength. It can be seen that the center por-
tion of the diaphragm is sampling the full value of the waveform, while
adjacent portions are sampling a slightly lesser value. Essentially, the
diaphragm will respond accurately, but with some small diminution of
output for the off-axis pickup angle shown here.

FIGURE 2–13

Theoretical polar response
for a free microphone
diaphragm open on both
sides. (Data presentation
after Beranek, 1954.)

Earg_02.qxd  14/9/04  2:35 PM  Page 20

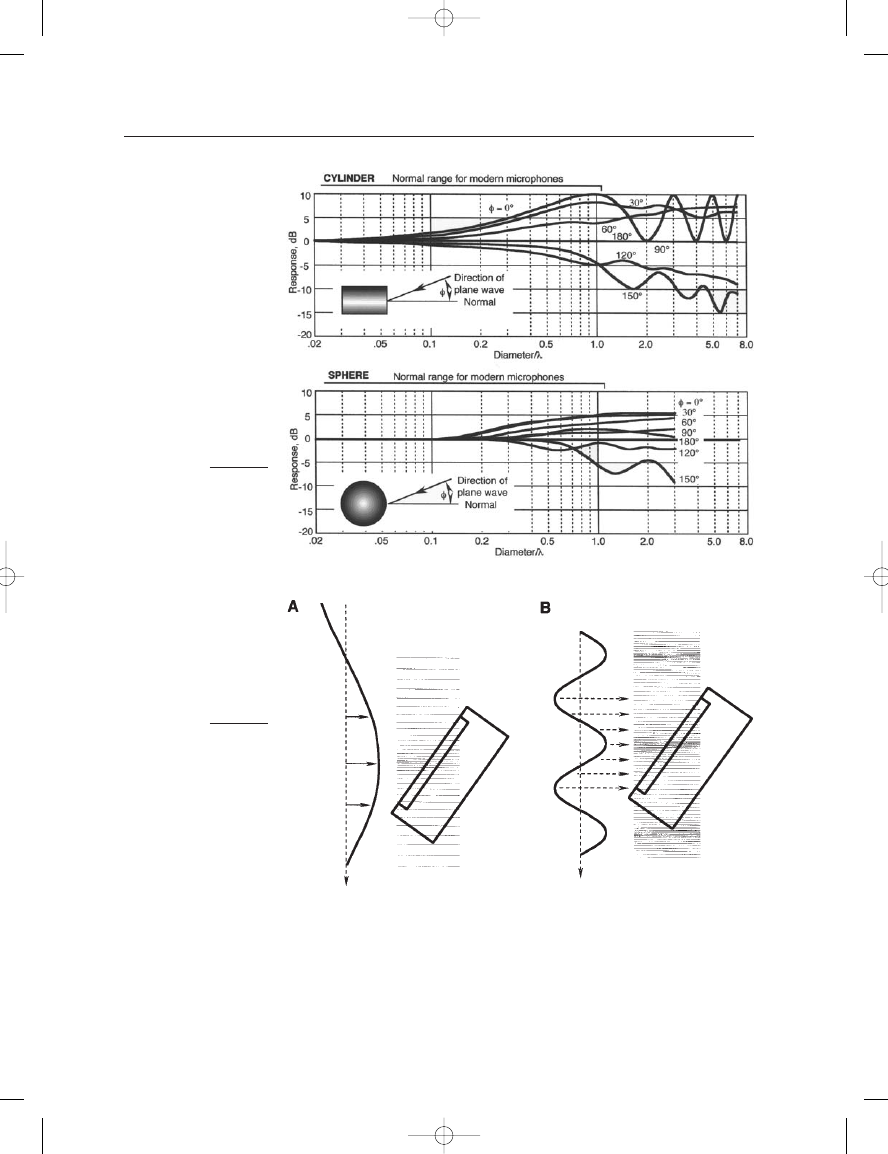
FIGURE 2–14

On and off-axis frequency
response for microphones
mounted on the end of a
cylinder and a sphere. (Data
after Muller et al., 1938.)

2: Basic Sound Transmission and Operational Forces on Microphones

21

The condition shown in Figure 2–15B is for an off-axis sound wave-

length which is equal to the subtended diameter of the microphone
diaphragm. Here, the diaphragm samples the entire wavelength, which
will result in near cancellation in response over the face of the
diaphragm.

FIGURE 2–15

Plane sound waves 
impinging on a microphone
diaphragm at an oblique
angle. Microphone
diaphragm subtended
diameter equal to 

/4 (A);

microphone diaphragm
subtended diameter equal 
to 

 (B). (Data after

Robertson, 1963.)

Earg_02.qxd  14/9/04  2:35 PM  Page 21

C

H

A

P

T

E

R

3

THE PRESSURE MICROPHONE

INTRODUCTION

An ideal pressure microphone responds only to sound pressure, with no
regard for the directional bearing of the sound source; as such, the
microphone receives sound through a single active opening. In reality, a
pressure microphone exhibits some directionality along its main axis at
short wavelengths, due principally to diffraction effects. As we saw in
Figure 2–12, only as the received wavelength approaches the circumfer-
ence of the microphone diaphragm does the microphone begin to depart
significantly from omnidirectional response. For many studio-quality
pressure microphones, this becomes significant above about 8 kHz.

The earliest microphones were of the pressure type, and the capaci-

tor pressure microphone is widely used today in music recording as well
as in instrumentation and measurement applications. By way of termi-
nology, the capacitor microphone is familiarly referred to in the sound
industry as the condenser microphone, making use of the earlier electri-
cal term for capacitor. We use the modern designation capacitor through-
out this book.

We begin with a study of the capacitor pressure microphone, ana-

lyzing it in physical and electrical detail. We then move on to a similar
analysis of the dynamic pressure microphone. Other transducers that
have been used in pressure microphone design, such as the piezoelectric
effect and the loose contact (carbon granule) effect, are also discussed.
The RF (radio frequency) signal conversion principle use in some capaci-
tor microphones is discussed in Chapter 8.

ANALYSIS OF THE CAPACITOR PRESSURE MICROPHONE

Figure 3–1 shows section and front views of a modern studio capacitor
pressure microphone capsule along with its associated electrical circuitry.
It is very similar to Wente’s original 1917 model (see Figure 1–7), except
that the modern design shown here is about one-third the diameter of the

Earg_03.qxd  14/9/04  2:37 PM  Page 22