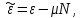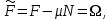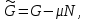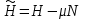Файл: Термодинамические потенциалы План.rtf

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 18

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

«Термодинамические потенциалы»
План:

  1. Группа потенциалов “E F G H”, имеющих размерность энергии.

  2. Зависимость термодинамических потенциалов от числа частиц. Энтропия как термодинамический потенциал.

  3. Термодинамические потенциалы многокомпонентных систем.

  4. Практическая реализация метода термодинамических потенциалов (на примере задачи химического равновесия).

1.

Один из основных методов современной термодинамики является метод термодинамических потенциалов. Этот метод возник, во многом, благодаря использованию потенциалов в классической механике, где его изменение связывалось с производимой работой, а сам потенциал является энергетической характеристикой термодинамической системы. Исторически сложилось так, что введенные первоначально термодинамические потенциалы также имели размерность энергии, что и определило их название.

Упомянутая группа включает следующие системы:

- внутренняя энергия ;

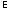- свободная энергия или потенциал Гельмгольца ;

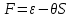- термодинамический потенциал Гиббса ;

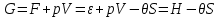- энтальпия .

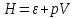Потенциальность внутренней энергии 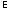была показано в предыдущей теме. Из нее следует потенциальность остальных величин.

Дифференциалы термодинамических потенциалов принимает вид:



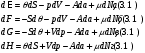
Из соотношений (3.1) видно, что соответствующие термодинамические потенциалы характеризуют одну и ту же термодинамическую систему при различных способах …. описания (способах задания состояния термодинамической системы). Так, для адиабатически изолированной системы, описываемой в переменных 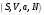удобно в качестве термодинамического потенциала использовать внутреннюю энергию .Тогда параметры системы, термодинамически сопряженные к потенциалам, определяются из соотношений: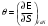

, ,
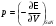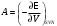
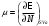, (3.2)

Если в качестве способа описания используется “система в термостате”, задаваемая переменными 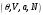, наиболее удобно использовать в качестве потенциала свободную энергию 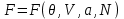. Соответственно, для параметров системы получим:

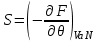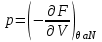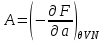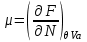, , , (3.3)

Далее, выберем в качестве способа описания модель “системы под поршнем”. В этих случаях функции состояния образуют набор ( 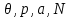), а в качестве термодинамического потенциала используется потенциал Гиббса G. Тогда параметры системы определяются из выражений:

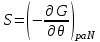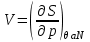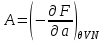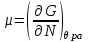, , , (3.4)

И в случае “адиабатической системы над поршнем”, заданной функциями состояния 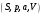роль термодинамического потенциала играет энтальпия H. Тогда параметры системы принимают вид:

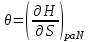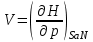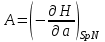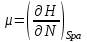, , , (3.5)

Из того, что соотношения (3.1) задают полные дифференциалы термодинамических потенциалов, мы можем приравнивать их вторые производные.

Например, 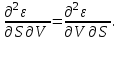Учитывая, что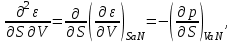



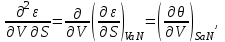
получаем

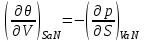(3.6а)

Аналогично для остальных параметров системы, связанных с термодинамическим потенциалом 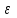, запишем:




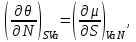
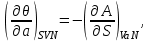
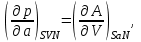
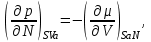
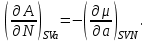(3.6б-е)

Подобные тождества можно записать и для других наборов параметров термодинамического состояния системы на основе потенциальности соответствующих термодинамических функций .

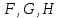Так, для “системы в термостате” c потенциалом 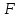, имеем:



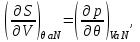
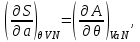
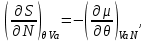
(3.7)



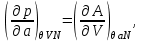
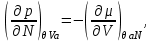
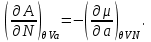
Для системы “над поршнем” с потенциалом Гиббса 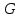будут справедливы равенства: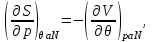



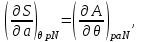
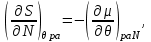
(3.8)



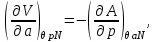
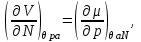
И, наконец, для системы с адиабатическим поршнем с потенциалом H, получим:



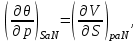
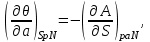
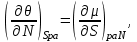
(3.9)



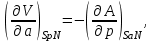
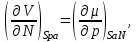
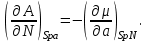
Равенства вида (3.6) – (3.9) получили название термодинамических тождеств и в ряде случаев оказываются удобными для практических расчетов.

Использование термодинамических потенциалов позволяет достаточно просто определить работу системы 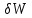и тепловой эффект .

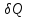Так, из соотношений (3.1) следует:


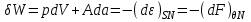(3.10)

Из первой части равенства следует известное положение о том, что работа теплоизолированной системы ( 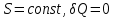) производится за счет убыли ее внутренней энергии. Второе равенство означает, что свободная энергия есть та часть внутренней энергии , которая при изотермическом процессе 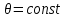целиком переходит в работу (соответственно “оставшуюся” часть внутренней энергии 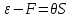иногда называют связанной энергией).

Количество теплоты можно представить в виде: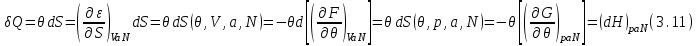

Из последнего равенства понятно, почему энтальпию еще называют теплосодержанием. При горении и других химических реакциях, происходящих при постоянном давлении ( 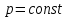), выделяемое количество теплоты равно изменению энтальпии.

Выражение (3.11), с учетом второго начала термодинамики (2.7) позволяет определить теплоемкость:



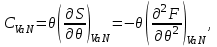
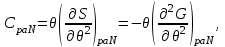
(3.12)



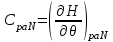
Все термодинамические потенциалы типа энергии обладают свойством аддитивности. Поэтому можно записать:



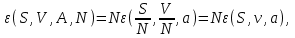
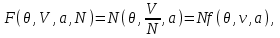(3.13)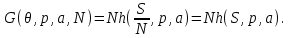



Легко видеть, что потенциал Гиббса содержит только один аддитивный параметр 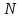, т.е. удельный потенциал Гиббса 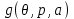от не зависит. Тогда из (3.4) следует:

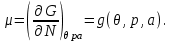(3.14)

То есть химический потенциал есть удельный потенциал Гиббса, и имеет место равенство


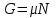(3.15)

Термодинамические потенциалы (3.1) связаны между собой прямыми соотношениями, позволяющими совершать переход от одних потенциалов к другим. Например, выразим все термодинамические потенциалы через внутреннюю энергию.



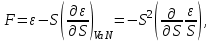
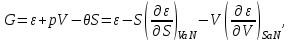(3.16)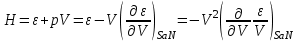



При этом мы получили все термодинамические потенциалы как функции ( ). Для того, чтобы выразить их в других переменных, используют процедуру пере….

Пусть задано давление 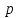в переменных ( ):

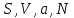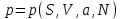(3.17)

Запишем последнее выражение в виде уравнения состояния, т.е. найдем вид



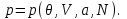
Легко видеть, что если состояние задано в переменных ( 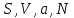), то термодинамическим потенциалом является внутренняя энергия 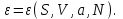В силу (3.2) найдем

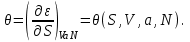(3.18)

Рассматривая (3.18) как уравнение относительно S, находим его решение:

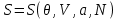(3.19)

Подставляя (3.19) в (3.17) получаем

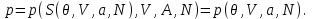(3.20)

То есть от переменных ( 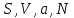) мы перешли к переменным ( ).

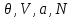2.

Вторая группа термодинамических потенциалов возникает в том случае, если в качестве термодинамических переменных, помимо рассмотренных выше, включен химический потенциал 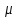. Потенциалы второй группы также имеют размерность энергии и могут быть связаны с потенциалами первой группы путем соотношений:

Смотрите также файлы