Лабораторная работа № 2
Определение момента инерции твердого тела.
Цель работы: определить момент инерции крестовины с грузами, используя законы динамики вращательного движения и сохранения энергии.
Приборы и принадлежности: маятник Обербека, грузы, масштабная линейка, секундомер, штангенциркуль.
Схема экспериментальной установки:


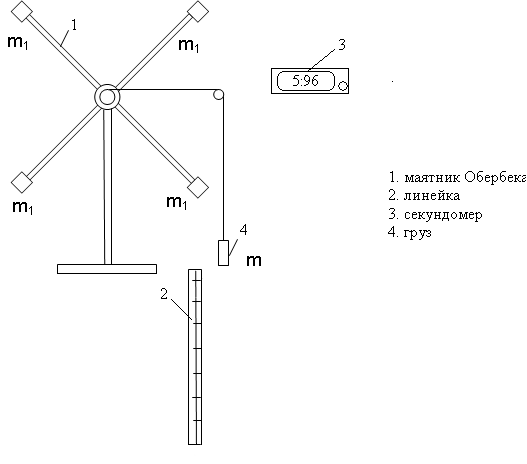
Теоретические сведения

Движение твердого тела, при котором все точки прямой ОО’ жестко связанной с телом, остаются неподвижными, называется вращением тела вокруг неподвижной оси ОО’.

Движение твердого тела, при котором только одна точка О остается все время неподвижной, называется вращением вокруг неподвижной точки О.

К кинематическим характеристикам вращательного движения относятся: угол поворота 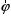, угловая скорость 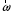и угловое ускорение .

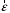Угловой скоростью вращения 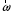называется первая производная от угла поворота по времени, то есть изменение угла поворота в единицу времени:

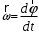. (1)

Угловым ускорением называется первая производная от угловой скорости по времени (угловое ускорение характеризует быстроту изменения угловой скорости):

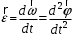. (2)

Динамической характеристикой вращательного движения является момент силы .


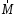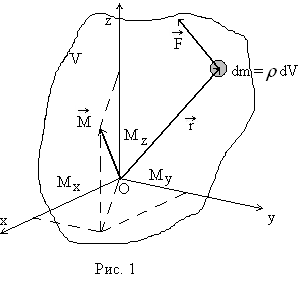
Моментом силы 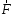относительно точки О называется векторное произведение

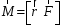, (3)

где 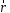- радиус-вектор, проведенный из точки О в точку приложения силы.

Моментом силы относительно оси называется скалярная величина

---

, равная проекции на данную ось вектора момента силы относительно какой-либо точки той же оси.

Момент инерции твердого тела J является физической величиной, характеризующей инертность тела при изменении угловой скорости вращения этого тела ω под действием вращающего момента М.

Для вычисления момента инерции вращающегося тела тело разбивают на элементарные объемы 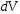с массой 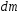, и алгебраически суммируют моменты инерции всех элементарных масс 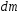, составляющих тело.

Для тела, имеющего постоянную плотностьρ, момент инерции может быть определён путем интегрирования:

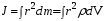, (4)

где dV - элемент объема;

r - расстояние от этого элемента до оси вращения.

Из формулы (4) видно, что момент инерции не зависит от характера движения, а зависит от размеров, форм и плотности тела, а также от расположения тела относительно оси вращения. Момент инерции твердого тела во вращательном движении выполняет ту же роль, что и масса тела при поступательном движении.

Проектирование машин и механизмов, имеющих вращающиеся при работе детали, ведется с учетом моментов инерции этих деталей.

Для однородного тела правильной геометрической формы момент инерции может быть вычислен теоретически (4). При сложной форме тела и неравномерном распределении плотности вещества в нем теоретическое вычисление момента инерции может быть достаточно сложной задачей. В этих случаях момент инерции определяют опытным путем. В настоящей работе определяется момент инерции крестовины маятника Обербека методом вращения.

Подвижная часть маятника Обербека (крестовина) состоит из двухступенчатого блока, насаженного на ось, и четырех спиц с одинаковыми цилиндрическими грузами с массами m₁. Грузы m₁ можно перемещать, закрепляя в том или ином положении, меняя этим момент инерции крестовины.

Центр тяжести системы должен находиться на оси вращения. Крестовина приводится в движение при помощи груза массой

---

m, прикрепленного на нити, накрученной на шкив.

Итак, если груз опустить с высоты h, то он будет двигаться с линейным ускорением:

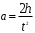, (5)

где t- время движения груза на участке длиной h.

Крестовина же при этом будет вращаться с угловым ускорением:

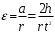, (6)

где r - радиус шкива, на который наматывается нить.

С другой стороны, это ускорение по закону динамики вращательного движения:

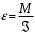, (7)

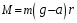, (8)

где g - ускорение свободного падения.

На основании (5), (6), (7), (8) получаем:

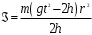. (9)
Порядок выполнения работы

Таблица вариантов

вариант параметр	1	2	3				4	5			6		7		8		9	10
положение грузов на штанге	первые пять опытов – центральное, а затем пять опытов крайнее					первые пять опытов – крайнее, а затем пять опытов среднее						первые пять опытов – среднее, а затем пять опытов центральное
m, г	100г	150г		200г	100г				150г	150г		100г		200г		200г			200г
r, м	0.0175	0.0300	0.0090				0.0175	0.0300			0.0090		0.0175		0.0300		0.0090	0.0175
h, м	0,8	0,9	1				0,8	0,9			1		0,8		0,9		1	0,8

---

1. Откройте flash - анимацию.

2. По указанию преподавателя в соответствии с таблицей вариантов с помощью мыши задайте параметры экспериментальной установки. Задание параметров необходимо начинать с h (высота, с которой опускается груз).

3. Запишите данные установки в таблицу.

4. Щелкните кнопку «Пуск» для начала эксперимента. Остановите секундомер с помощью мыши в момент касания грузом нулевого уровня.

5. Занесите полученное значение времени в таблицу.

6. Повторите опыт 10 раз, каждый раз вводя параметры установки.

7. При помощи калькулятора произведите вычисления предлагаемых величин.

8. Сделайте вывод о проделанной работе и ответьте на контрольные вопросы.
Обработка результатов измерений
1. Абсолютные погрешности времени определить как погрешность секундомера.

2. Момент инерции рассчитать по формуле (9).

3. Относительные погрешности опытов определить по формуле

.

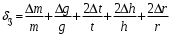4. Абсолютные погрешности опытов рассчитать по формуле

.

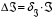Таблица измерений

Номер опыта	m…	h…	t…	t…	r…	r…	…	…	…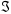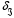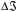
1	0,2	0,8	7,84	0,005	0,0175	0,0005	0,0230	0,0627	0,0014
2	0,2	0,8	7,62	0,005	0,0175	0,0005	0,0217	0,0627	0,0014
3	0,2	0,8	7,5	0,005	0,0175	0,0005	0,0211	0,0627	0,0013
4	0,2	0,8	7,26	0,005	0,0175	0,0005	0,0197	0,0628	0,0012
5	0,2	0,8	6,94	0,005	0,0175	0,0005	0,0180	0,0628	0,0011
6	0,2	0,8	4,8	0,005	0,0175	0,0005	0,0086	0,0635	0,0005
7	0,2	0,8	4,6	0,005	0,0175	0,0005	0,0079	0,0636	0,0005
8	0,2	0,8	4,58	0,005	0,0175	0,0005	0,0078	0,0636	0,0005
9	0,2	0,8	4,78	0,005	0,0175	0,0005	0,0085	0,0635	0,0005
10	0,2	0,8	4,48	0,005	0,0175	0,0005	0,0075	0,0636	0,0005
Среднее значение	-	-	-	-	-	-	0,0207	0,0628	0,0013
							0,0081	0,0636	0,0005

---

1,Что называется моментом инерции материальной точки и абсолютно твердого тела?

Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость.

2,Что называется моментом силы относительно неподвижной точки и неподвижной оси, как он направлен, как определяется его модуль?
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора   момента силы, определенного относительно произвольной точки О данной оси z. Значение момента Мz не зависит от выбора положения точки О на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:  =[ ]z.

3) Запишите основной закон динамики вращательного движения.

Вращательное движение тела отличается от поступательного тем, что все уравнения, описывающие движения и взаимодействие тел, учитывают центр вращения, и все величины в этих уравнениях берутся относительно этого центра. Рассмотрим основной закон динамики вращательного движения. Динамика изучает причины движения тел. И основной закон динамики – Второй Закон Ньютона – связывает ускорение, получаемое телом, с силой, действующей на тело.

Для прямолинейного движения основной закон динамики записывается следующим образом:

a→=F→ma→=F→m

То есть, ускорение, получаемое телом, прямо пропорционально силе, действующей на тело (точнее, равнодействующей всех сил) и обратно пропорционально массе тела. Направлено это ускорение в ту же сторону, в которую направлена и сила.

---

Смотрите также файлы

• Юпитер. Общая характеристика.docx

• Практическое задание 1 Практическое задание Конвергентный подход в образовании.docx

• Контрольные вопросы Сущность и значение кредитной формы функционирования государственных и муниципальных финансов.docx

• Образовательная программа по специальности 51. 02. 02 Социальнокультурная деятельность Форма обучения заочная.docx

• Тема оценка правильности сегментации рынка.docx