Файл: Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования по дисциплине Гидравлика и нефтегазовая гидромехпника.docx

2 Гидравлический расчет разветвленного трубопровода

Выполнить гидравлический расчет разветвленного трубопровода, схема которого прилагается.

1) Определить P_вх и d₃, d₄, из условия, что Q₃ = 1,5Q₄

2) Как изменятся расходы при изменении вязкости в 2,5 раза?



Проектный расход, м³/час Q₁ = Q₂ = 280___________________

Перекачиваемая жидкость ρ = 890 кг/м³; υ = 18*10^-6 м²/c

Эквивалентная шероховатость_К_э=0,06 мм_____________

№	l, м	d, мм	zн,м	zк,м	рн, кПа	рк,кПа	Q,м3/ч	Примечание
1	30	200	6	0	1,2	Pвх-?	280
2	300	180	0	ZM	490	РМ	280
3	420	?	ZM	7	РM	2	1,5Q4
4	280	?	ZM	6	РM	2	Q4

---

2.1 Определение входного давления на насос

Данную схему можно разбить на 4 простых трубопровода, причем трубопровод 1 (l₁, d₁) является всасывающим и рассчитывается отдельно от сложного трубопровода, состоящего из трубы 2 (l₂, d₂), трубы 3 (l₃, d₃) и трубы 4 (l₄, d₄).

Составим уравнение Бернулли для трубопровода 1. При этом начальное сечение соответствует свободной поверхности жидкости в первом резервуаре, а конечное сечение – на входе в насос.

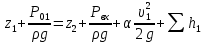(2.1)

где 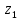– высотная отметка начального сечения;

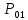– избыточное давление на свободной поверхности в первом резервуаре;

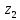– высотная отметка входа в насос.

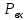– избыточное давление на входе в насос;

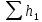– суммарные потери напора в первом трубопроводе.

Средняя скорость движения жидкости в первом трубопроводе равна:

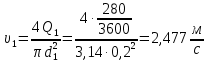(2.2)

Рассчитываем число Рейнольдса:

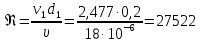(2.3)

Рассчитываем переходные числа Рейнольдса:

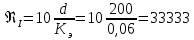(2.4)

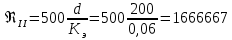(2.5)

Полученное число Рейнольдса Re_кр=2300 <Re< Re_I. Из чего следует, что в первом трубопроводе турбулентный режим течения, зона гладких труб.

Коэффициент гидравлического сопротивления 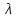определяем по формуле Блазиуса:

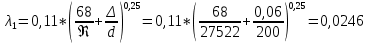(2.6)

Рассчитываем суммарные потери напора во втором трубопроводе:

---

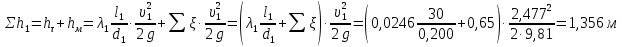
(2.7)

где 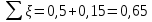(вход в трубу, полностью открытая задвижка).

Из уравнения Бернулли определяем :

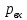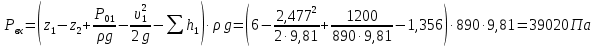. (2.8)

2.2 Определение потерей напора в 3 и 4 трубопроводе.
Составим систему уравнений Бернулли для разветвленной части трубопроводной сети.

Для трубопровода 2:

,

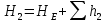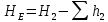, (2.9)

Для трубопровода 3:

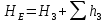, (2.10)

Для трубопровода 4:

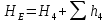, (2.11)

Где ;

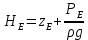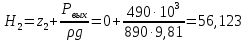м; (2.12)

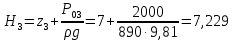м; (2.13)

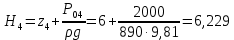м. (2.14)

Уравнения расходов:

Q₁ = Q₂ = Q

Q = Q₃ + Q₄

Полученные уравнения сведем в систему:



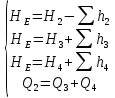
Средняя скорость жидкости в трубопроводе 2 равна:

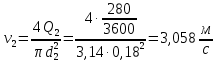Рассчитываем число Рейнольдса:

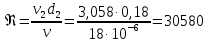Рассчитываем переходные числа Рейнольдса:

, .

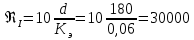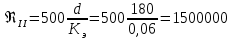Полученное число Рейнольдса Re_I <Re< Re_II. Из чего следует, что в первом трубопроводе турбулентный режим течения, зона смешанного трения труб.

Коэффициент гидравлического сопротивления определяем по формуле Альтшуля: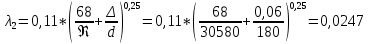



Рассчитываем суммарные потери напора во втором трубопрово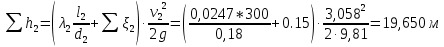де:

где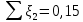 (полностью открытая задвижка).

Из уравнения (1) определяем :

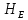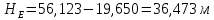(2.15) Из уравнений (2) и (3) выражаем суммарные потери напора в третьем и четвертом трубопроводе: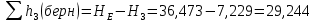

м, (2.16)

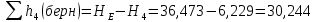м. (2.17)

Найдем диаметры третьего и четвертого трубопроводов.
Гидравлическая характеристика трубопровода № 3

Q­₃ = 1,5Q₄ , значит Q₄ = 280/2,5 = 112 м³/ч, Q₃ = 112*1,5 = 168 м³/ч

При диаметре трубопровода 100 мм:



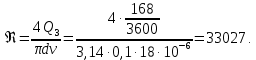
Рассчитываем переходные числа Рейнольдса





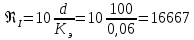
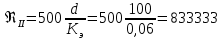
Полученное число Рейнольдса Re_I< Re < Re_II. Из чего следует, что в первом трубопроводе турбулентный режим течения, зона смешанного трения.

Коэффициент гидравлического сопротивления определяем по формуле Альтшуя: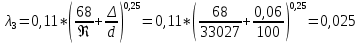



Средняя скорость движения жидкости в трубопроводе равна:



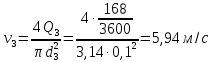
Суммарные потери напора в трубопроводе 3:



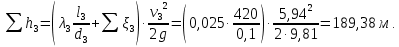
Аналогичные действия выполняются для других диаметров (таблица 1).
Таблица 1 – Данные для построения гидравлической характеристики трубопровода № 3

№ п/п	d3, мм	Re	ReI	ReII	λ3	υ3, м/с	h, м
1	100	33027	16666,667	833333,3	0,0250	5,94	189,38
2	110	30024	18333,333	916666,7	0,0253	4,91	119,25
3	120	27522	20000	1000000	0,0257	4,13	78,28
4	130	25405	21666,667	1083333	0,0260	3,52	53,19
5	140	23590	23333,333	1166667	0,0264	3,03	37,22
6	150	22018	25000	1250000	0,0260	2,64	25,96
7	160	20642	26666,667	1333333	0,0264	2,32	19,11

Гидравлическая характеристика трубопровода № 4 будет находиться таким же образом, как и для трубопровода № 3 (таблица 2).
Таблица 2 – Данные для построения гидравлической характеристики трубопровода № 4

№ п/п	d4, мм	Re	ReI	ReII	λ4	υ4, м/с	h4, м
1	100	22018	16666,667	833333,3	0,0271	3,96	60,95
2	110	20016	18333,333	916666,7	0,0276	3,28	38,49
3	120	18348	20000	1000000	0,0272	2,75	24,58
4	130	16937	21666,667	1083333	0,0277	2,35	16,81
5	140	15727	23333,333	1166667	0,0283	2,02	11,82
6	150	14679	25000	1250000	0,0287	1,76	8,52
7	160	13761	26666,667	1333333	0,0292	1,55	6,27

На оси ординат откладываем величины 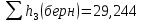м и 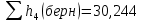м, и проводя горизонталь до пересечения с построенной кривой Σh_i(d_i), получаем соответствующее значение диаметра (Рисунок 3).

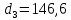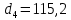мм, мм,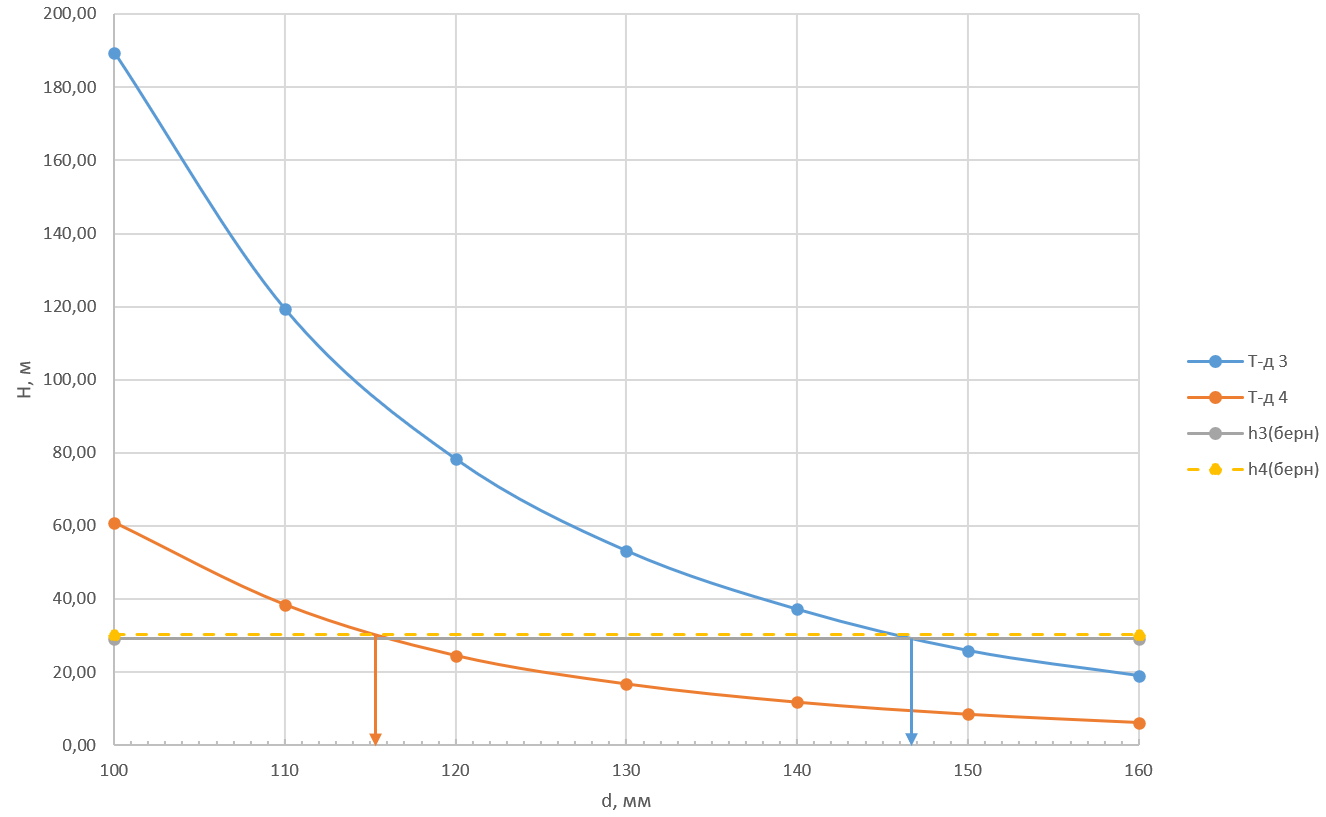

Рисунок 3 – Зависимости потерь напора от диаметра в трубопроводах

№ 3 и № 4

---

2.3 Определение расходов при изменении вязкости

Проверим зависимость расходов от вязкости, построив гидравлические характеристики труб, по которым течет жидкость с вязкостью в 2,5????. Новая вязкость примет значение ???? = 45*10^-6 м²/c. Будем считать, что давление на выходе из насоса осталось прежним.

Составим уравнение Бернулли для трубопроводов 2, 3, 4, относительно плоскости отсчета. При этом начальное сечение трубопровода 2 соответствует выходу из насоса, а конечное сечение – в т.Е. Для трубопроводов 3, 4 начальное сечение находится в т.Е, а конечное сечение – на входе в резервуары 3, 4 соответственно.





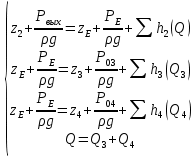
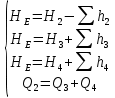
Где ;

м;

м;

м.

Для решения полученной системы уравнений рассчитаем гидравлические характеристики каждого трубопровода.

Рассчитаем потери напора в каждой из труб по формуле:



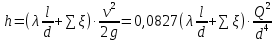
Для каждого значения расхода Q рассчитываем число Рейнольдса:



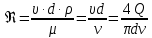
Сравнивая полученное число Рейнольдса с критическим Re_кр = 2320 и граничными (переходными) числам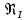и и 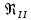(граничные числа Рейнольдса – Re_I и Re_II для всех трубопроводов остались прежними (см. задание 2)), определяем режим движения (ламинарный или турбулентный) и, в случае турбулентного режима, зону гидравлического сопротивления (гладких труб, смешанного трения, шероховатых труб).

Если число Рейнольдса Re < Re_кр=2320, то режим движения ламинарный, и λ определяем по формуле Стокса:



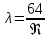
Если 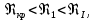то

---

режим движения турбулентный, зона гладких труб, и λ определяем по формуле Блазиуса:



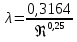
Если 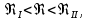то режим движения турбулентный, зона смешанного трения, и λ определяем по формуле Альтшуля: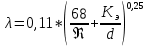



Если 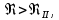то режим движения турбулентный, зона шероховатого трения, и λ определяем по формуле Шифринсона: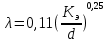



Составим гидравлические характеристики трубопроводов, с учетом зоны трения и расчета коэффициента гидравлических сопротивлений по соответствующим формулам.

Зададимся расходом в трубопроводе 3 :















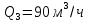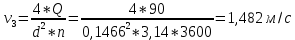
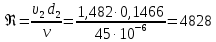
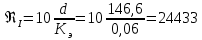
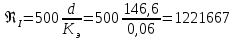
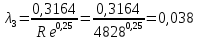
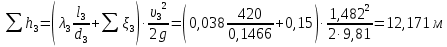
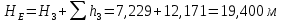
Аналогичные расчеты выполняются при других средних скоростях жидкости в трубопроводе 3 (таблица 3).

Таблица 3 – Данные для построения гидравлической характеристики трубопровода №3

№	Q, м3/с	v, м/с	Re	ReI	ReII	λ	h, м	HЕ, м
1	0	0	0	24433,33	1221667	0	0,00	7,229
2	30	0,494	1609	24433,33	1221667	0,0398	1,417	8,646
3	60	0,988	3218	24433,33	1221667	0,0420	5,986	13,215
4	90	1,482	4828	24433,33	1221667	0,0380	12,171	19,400
5	120	1,976	6437	24433,33	1221667	0,0353	20,136	27,365
6	150	2,470	8046	24433,33	1221667	0,0334	29,755	36,984
7	180	2,964	9655	24433,33	1221667	0,0319	40,938	48,167
8	210	3,458	11264	24433,33	1221667	0,0307	53,615	60,844

---