(Всю нижеприведенную лажу (в смысле, сам курсовик) нагнал студент. Сие творение было сдано 6 мая на оценку «отлично» без особых проблем, чего и вам желаю. Аминь.)(
Нижегородский государственный

технический университет

ПОЯНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту
__________________________________________

(фамилия, имя, отчество)
Факультет_________________________________

Кафедра ИРС
Группа___________________________________
Дата защиты “______” ________________2015г.


Чуть не забыл. Схему фильтра на А3 сдергивайте со стенда перед кабинетом Ногина. Если этот старпер спросит, откуда взята спецификация элементов, заткните его, сказав, что все взято с вышеупомянутого стенда. Вот теперь все. Фенита, бля, комедия!) Нижегородский Государственный Технический Университет Кафедра Информационных РадиосистемПОЯСНИТЕЛЬНАЯ ЗАПИСКА к курсовому проекту по схемотехнике аналоговых электронных устройств на темуАктивный узкополосный полосовой RC-фильтр Руководитель____________ __Когтева Л.В. ___(подпись) (фамилия, и.о.)Студент____________ ___ Давыдов Д.В ___(подпись) (фамилия, и.о.)_____С-12РЭС_____(группа или шифр)Проект защищен _____________________с оценкой ___________________________2015 г

Оглавление

Техническое задание

---

1. 
   Узкополосный полосовой АФ на ОУ;
   
2. 
   Резонансная частота f₀= 100 Гц;
   
3. 
   Коэфициент передачи К_рез= 30;
   
4. 
   Полоса пропускания ∆f=40 Гц;
   
5. 
   Амплитуда выходного напряжения U_вых= 4 В;
   
6. 
   Сопротивление нагрузки R_н= 200 Ом.
   

1. 
   Анализ технического задания
   

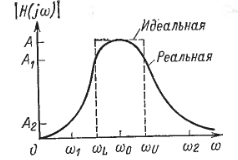
1.1 Общий случайРис. 1.1Полосно-пропускающий фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы ∆f, расположенной приблизительно вогруг центральной частоты ω₀ (рад/с), или f₀=ω₀/2π (Гц). На рис. 1.1 изображена идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты ω_н и ω_в представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания и ее ширину В полосе пропускания амплитудно-частотная характеристика никогда не находится ниже некоторого определенного значения, например А₁ на рис. 1.1. Существуют также две полосы задерживания 0≤ω≤ω₁ и ω≥ω₂, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, скажем, А₂. Диапазоны частот между полосами задерживания и полосой пропускания, а именно ω₁<ω<ω_н и ω_в<ω<ω_в, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.Отношение Q= характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q – относительно большая ширина полосы пропускания. Коэффициент усиления фильтра К определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом К=

---

.Передаточные функции полосно-пропускающих фильтров можно получить из нормированных функций нижних частот переменной S, см. [2] с помощью преобразования .(1.1)1.2 Передаточные функцииТак как передаточные функции полосно-пропускающих фильтров получаются с помощью использования преобразования вида (1.1) соответствующих функций нижних частот, то передаточная функция полосно-пропускающего фильтра будет состоять из произведения сомножителя функции нижних частот. Для сомножителя функции нижних частот первого порядка (1.2)Соответствующий сомножитель полосно-пропускающего фильтра представляет собой функцию второго порядка вида , (1.3)где С- нормированный коэффициент соответствующего звена нижних частот первого порядка, приведенный в приложении А [2] для фильтров Баттерворта и Чебышева, в приложении Б [2] – для инверсного фильтра Чебышева и в приложении В [2] - для эллиптического фильтра.Полосно-пропускающий фильтр второго порядка получается в том случае, когда соответствующий фильтр нижних частот имеет первый порядок. Таким образом, эта функция нижних частот описывается единственным уравнением (1.2) с С=1. В этом случае из (1.3) получаем передаточную функцию (1.4)Полосно-пропускающего фильтра второго порядка.Передаточную функцию вида (1.4) можно определить как функцию полосно-пропускающего фильтра Баттерворта или Чебышева второго порядка, поскольку уравнение (1.2) при С=1 описывает функцию Баттерворта или масштабированную функцию Чебышева нижних частот первого порядка. Однако на (1.4) обычно ссылаются как на передаточную функцию полосно-пропускающего фильтра второго порядка, а их наименования, а именно Баттерворта, Чебышева, инверсная Чебышева, и эллиптическая, используют дл полосно-пропускающих фильтров более высокого порядка.

---

Т 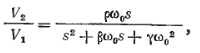иповую передаточную функцию полосно-пропускающего фильтра второго порядка можно записать в следующем виде:(1.5)где параметры β, γ, и ρ получаются с помощью приравнивания уравнения (1.5) к уравнению (1.3).1.3 Полосно-пропускающие фильтры с многопетлевой обратной связью и бесконечным коэффициентом усиления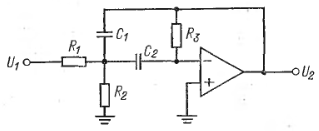Рис. 1.2 Схема полосно-пропускающего фильтра с МОС и бесконечным коэффициентом усиленияСхема с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления, изображенная на рис. 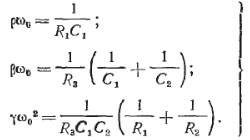1.2, представляет собой один из наиболее простых полосно-пропускающих фильтров второго порядка.Она реализует функцию полосно-пропускающего фильтра (1.5) при инвертирующем коэффициенте усиления ( для ρ>0 получаем значение –ρ), где (1.6)

2. Расчет элементов схемы

Для реализации полосового фильтра выбираем схему на основе каскадного соединения фильтра на ОУ1 с многопетлевой обратной связью (см. рис. 1.2) с коэффициентом передачи К1=1 и усилителя на ОУ2 с коэффициентом передачи К2=30.Общий коэффициент передачи К=К1*К2=30.2.1. Расчет каскада активного фильтраВыбираем ОУ1 для фильтра по частоте среза:F_в ОУ1 ≥ f_в = 120 Гц.Для ОУ1 типа К140УД23, частота среза более 1МГц т.о. последнее неравенство выполняется с запасом. По справочнику [4], Rвх ОУ1 более 1 МОм, т.е. номиналы резисторов в схеме фильтра должны находится в пределах от 100 к Ом до 1 к Ом. Выбрано двухполярное напряжение питания +10 В и -10 В.Круговая частота резонанса определяется:

1. 
   ω₀ = 2πf₀= 6.28*100= 628 рад/с
   

2. 
   Передаточная функция задаваемая уравнением 5.5 имеет вид:
   

(2.1)

3. 
   Сравнивая ее с (1.5) находим, что β=0.4,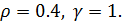
   

---

4. 
   Выбираем произвольно номинальное значение емкости С₁=0.68мкФ (принимаем стандартный номинал из ряда Е24 0,68 мкФ) и номинальное значение сопротивления R₃=100 кОм (принимаем стандартный номинал из ряда Е192 100 кОм)
   
5. 
   Вычисляем емкость С₂
   

(0.043 мкФ из ряда Е24)

6. 
   Вычисляем сопротивление R₂
   

(104 кОм из ряда Е192)

7. 
   Вычисляем сопротивление R₁
   

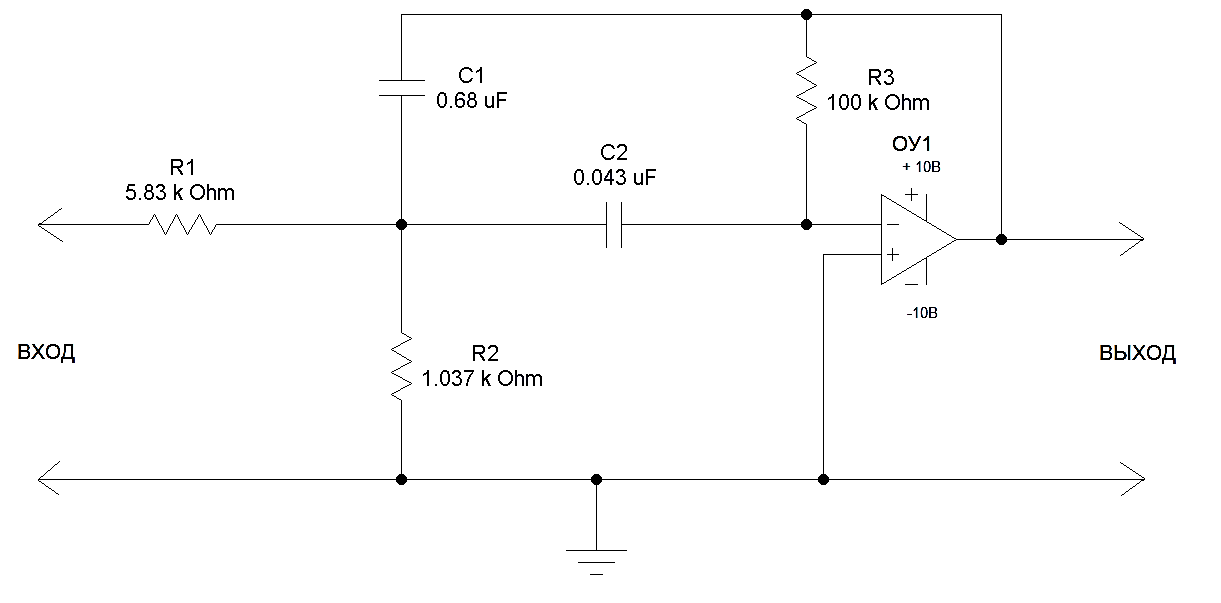
=5850 Ом (5.83 кОм из ряда Е192)Рис. 2.1 Схема активного фильтра ОУ1.2.2. Расчет усилителя Рассчитаем выходную мощность выделяемую на нагрузке(2.2)Ток нагрузки (пиковый)(2.3)Выбираем ОУ по максимальному возможному току, ОУ2 для усилителя выбираем в справочнике [5] К174УН14, т.к. 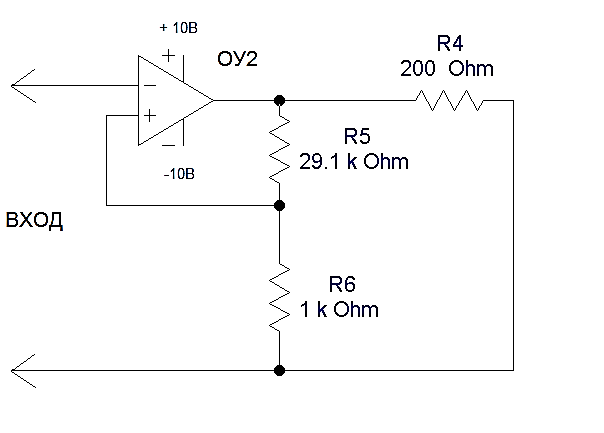.Входное сопротивление ОУ2 больше 100 кОм, минимальное сопротивление нагрузки 4 Ом, при двухполярном напряжении питания +10 В и -10 В.Коэффициент передачи второго звена будет: К2=1+Выбираем R6=1 кОм (1 кОм из ряда Е192), тогда для получения нужного К2=30, резистор R5 должен иметь значение сопротивления R5=29 кОм (29.10кОм из ряда Е192).Рис. 2.2 Схема усилителя мощности ОУ2

3. АЧХ схемы и осциллограмма сигнала на нагрузке

---

Смотрите также файлы

• Задание 1 Рационализм это направление в философии, согласно которому основой как бытия, так и познания является разум. Эмпиризм.docx

• Анализ схемотехники пересчетного устройства.docx

• Виды, формы и организация контроля качества обучения. Понятие контроля. Функции контроля. Требования к контролю.docx

• Мшелер жне мшелер жйесі.docx

• Анализ схемотехники умножителя частот.docx