Файл: Решение Пусть а множество абитуриентов, выдержавших экзамен.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 14
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждения высшего образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Факультет фундаментальной и прикладной информатики
Кафедра Инфокоммуникационные технология и система связи
Исполнитель
студент группы ИТ-22б
Ашыров.А.Р
Проверяющий, профессор д.физ.мат
Добрица В.П.
Курск 2023
Практическое занятие №4
Формула включений и исключений и бином Ньютона
Цель: Изучить методику использования формулы включений и исключений для решения задач по определению количества элементов в множестве. Изучить методику разложения выражения
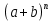по формуле бинома Ньютона.Вопросы, выносимые на практическое занятие.
-
Формула включений и исключений. -
Формула бинома Ньютона. -
Свойства биномиальных коэффициентов.
Треугольник Паскаля.
-
Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти получили 180 человек, а выдержали экзамен 210 абитуриентов.
Сколько человек получили оценки 3 и 4?
Решение:
Пусть А – множество абитуриентов, выдержавших экзамен,
В – множество абитуриентов, получивших оценку ниже 5, по условию
m (A)=210,
m (В)=180,
m (A
B)=250. Абитуриенты, получившие оценки 3 и 4, образуют множество А∩В.
Находим m (A∩B) = m (A) + m (В) - m (A
B) = 210 + 180 – 250 = 140.2.В течении недели по телевизору демонстрировались фильмы: боевик А, вестерн В и мелодрама С. Из 40 студентов, каждый из которых просмотрел либо все три фильма, либо один из трех, фильм А видели 13, фильм В - 16, фильм С -19. Найдите, сколько учеников просмотрели все три фильма.
Решение:
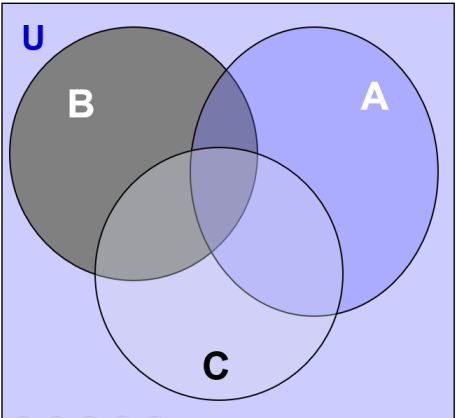
m(A*B) = 25+22-33=14
m(A*C)= 25+22-32=15
m(B*C)=25+22-31=16
m(A*C*B)=25+22+22-14-15-16+10=34
m(U)=40-34=6
m(0)=34-14-15-16+20=9