Файл: Федеральное государственное бюджетное образовательное учереждение высшего образования дальневосточный государственный университет путей сообщения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 32
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра «Транспорт железных дорог»
РАСЧЁТ ТЕПЛОПЕРЕДАЧИ
Расчётно-графическая работа по дисциплине «Термодинамика и теплопередача»
РГР 23.05.03.23 СО131ВАГ 02
Студент В. Г. Якименко
Руководитель И.Д. Конькова
Хабаровск – 2021
Исходные данные для расчёта теплопередачи:
Среда 1 (внутри трубы) – масло авиационное
Скорость W1 = 2 м/c
Температура T1 = 100 oC
Среда 2 (снаружи трубы) – воздух
Скорость W2 = 0,15 м/c
Температура T2 = -20 oC
Поток воздуха направлен под углом 60 oC к оси трубы
Внутренний диаметр трубы D1 = 30 мм
Толщина трубы ∂1 = 4 мм
Толщина трубы ∂2 = 6 мм
Материал изоляции: Глина
Металл трубы: Цинк
Решение:
1.1. Расчет теплоотдачи от жидкости к стенке трубы
Наружные диаметры труб, мм, рассчитываются по формулам:
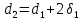 ; (1.1)
; (1.1)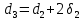 , (1.2)
, (1.2)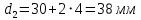
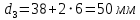
где
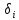 – толщина стенки трубы, мм.
– толщина стенки трубы, мм.Коэффициент теплоотдачи между жидкостью и внутренней стенкой трубы, Вт/(м2·К), определяется по формуле
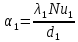 , (1.3)
, (1.3)Так как число Рейнольдса определяет характер режима течения теплоносителя и выражает отношение сил инерции (скоростного напора) к силам вязкого трения. При течении жидкости в трубах, переходной режим течения имеет место при 2,3

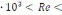 103
103 
 104 Значит Коэффициент теплоотдачи между жидкостью и внутренней стенкой трубы будет определяться по переходному режиму течения.
104 Значит Коэффициент теплоотдачи между жидкостью и внутренней стенкой трубы будет определяться по переходному режиму течения.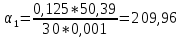
где
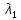 – коэффициент теплопроводности жидкости, Вт/(м
– коэффициент теплопроводности жидкости, Вт/(м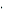
 К);
К); 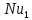 – число Нуссельта для жидкости в ламинарном режиме течения;
– число Нуссельта для жидкости в ламинарном режиме течения; 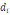
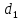 – характерный размер поверхности теплоотдачи (для труб – диаметр, омываемый теплоносителем), м.
– характерный размер поверхности теплоотдачи (для труб – диаметр, омываемый теплоносителем), м.Для определения числа Нуссельта при течении жидкости в трубах рекомендуются следующие расчетные формулы (критериальные зависимости):
– при ламинарном режиме течения
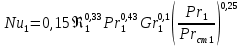 ; (1.4)
; (1.4)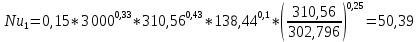 ;
;где
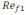
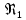 – число Рейнольдса, определяемое при температуре жидкости; Pr1 – число Прандтля, определяемое при температуре жидкости;
– число Рейнольдса, определяемое при температуре жидкости; Pr1 – число Прандтля, определяемое при температуре жидкости; Prст1 – число Прандтля, определяемое при температуре внутренней поверхности трубы (при расчете температуру стенки трубы
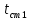 можно принять на 0,5…3 ºС меньше, чем температура теплоносителя t1);
можно принять на 0,5…3 ºС меньше, чем температура теплоносителя t1); Gr1 – число Грасгофа, определяемое при температуре жидкости;
K0
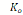 – поправочный коэффициент для переходного режима течения (значения поправочного коэффициента приведены в табл. 1).
– поправочный коэффициент для переходного режима течения (значения поправочного коэффициента приведены в табл. 1).Таблица 1
Значения поправочного коэффициента K0
| Ref | 2,5 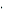  103 103 | 3 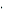  103 103 | 4 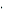  103 103 | 5 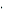  103 103 | 6 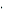  103 103 | 7 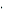  103 103 | 8 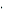  103 103 | 9 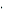  103 103 |
| Grƒ= 100 | 4 | 7 | 11 | 15 | 19 | 23 | 26 | 29 |
| Grƒ= 102 | 5 | 8 | 12 | 16 | 20 | 24 | 27 | 30 |
| Grƒ= 104 | 6 | 9 | 13 | 17 | 21 | 25 | 28 | 31 |
| Grƒ= 106 | 7 | 10 | 14 | 18 | 22 | 26 | 29 | 32 |
Число Рейнольдса рассчитывается по формуле


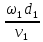 , (1.6)
, (1.6)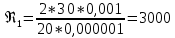
где
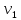 – кинематическая вязкость жидкости, м2/с. Значения кинематической вязкости в зависимости от температуры приведены в табл. 2.
– кинематическая вязкость жидкости, м2/с. Значения кинематической вязкости в зависимости от температуры приведены в табл. 2.Таблица 2
Физические свойства жидкостей в зависимости от температуры
| t, ºС | 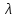 , Вт/(м·К) , Вт/(м·К) | 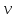 ·106, м2/с ·106, м2/с | 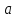 ·108, м2/с ·108, м2/с | 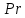 | 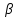 ·104, 1/К ·104, 1/К |
| Вода на линии насыщения | |||||
| 10 | 0,575 | 1,306 | 13,7 | 9,52 | 0,70 |
| 20 | 0,559 | 1,006 | 14,3 | 7,00 | 1,82 |
| 30 | 0,618 | 0,805 | 14,9 | 5,41 | 3,21 |
| 40 | 0,634 | 0,658 | 15,3 | 4,30 | 3,37 |
| 50 | 0,648 | 0,556 | 15,7 | 3,54 | 4,49 |
| 60 | 0,659 | 0,478 | 16,1 | 2,98 | 5,11 |
| 70 | 0,668 | 0,415 | 16,3 | 2,55 | 5,70 |
| 80 | 0,674 | 0,366 | 16,6 | 2,21 | 6,32 |
| 90 | 0,680 | 0,326 | 16,8 | 1,95 | 6,95 |
| 100 | 0,683 | 0,294 | 16,9 | 1,75 | 7,52 |
| Масло дизельное М | |||||
| 10 | 0,128 | 1520 | 7,75 | 19613 | 6,26 |
| 20 | 0,127 | 620 | 7,63 | 8126 | 6,30 |
| 30 | 0,127 | 280 | 7,49 | 3738 | 6,34 |
| 40 | 0,126 | 135 | 7,36 | 1834 | 6,38 |
| 50 | 0,125 | 76 | 7,25 | 1048 | 6,42 |
| 60 | 0,125 | 46 | 7,14 | 644 | 6,46 |
| 70 | 0,124 | 29 | 7,02 | 413 | 6,50 |
| 80 | 0,123 | 20 | 6,90 | 290 | 6,54 |
| 90 | 0,123 | 14 | 6,81 | 206 | 6,58 |
| 100 | 0,122 | 12 | 6,70 | 179 | 6,62 |
| Масло авиационное МС | |||||
| 10 | 0,135 | 2200 | 7,44 | 29570 | 6,31 |
| 20 | 0,134 | 1125 | 7,30 | 15400 | 6,35 |
| 30 | 0,132 | 526 | 7,19 | 2310 | 6,38 |
| 40 | 0,131 | 276 | 7,08 | 3890 | 6,42 |
| 50 | 0,130 | 153 | 7,00 | 2180 | 6,46 |
| 60 | 0,129 | 92 | 6,86 | 1340 | 6,51 |
| 70 | 0,128 | 58 | 6,75 | 865 | 6,55 |
| 80 | 0,127 | 39 | 6,67 | 588 | 6,60 |
| 90 | 0,126 | 28 | 6,56 | 420 | 6,64 |
| 100 | 0,125 | 20 | 6,44 | 315 | 6,69 |
Окончание табл. 2
| t, ºС |  , Вт/(м·К) , Вт/(м·К) |  ·106, м2/с ·106, м2/с |  ·108, м2/с ·108, м2/с |  |  ·104, 1/К ·104, 1/К |
| Масло трансформаторное Т | |||||
| 10 | 0,112 | 38 | 7,83 | 484 | 6,85 |
| 20 | 0,111 | 23 | 7,56 | 298 | 6,90 |
| 30 | 0,110 | 15 | 7,28 | 202 | 6,95 |
| 40 | 0,109 | 10 | 7,03 | 146 | 7,00 |
| 50 | 0,108 | 8 | 6,80 | 111 | 7,05 |
| 60 | 0,107 | 6 | 6,58 | 88 | 7,10 |
| 70 | 0,106 | 5 | 6,36 | 71 | 7,15 |
| 80 | 0,105 | 4 | 6,17 | 59 | 7,20 |
| 90 | 0,104 | 3 | 6,00 | 51 | 7,25 |
| 100 | 0,103 | 2 | 5,83 | 44 | 7,30 |
Число Рейнольдса определяет характер режима течения теплоносителя и выражает отношение сил инерции (скоростного напора) к силам вязкого трения. При течении жидкости в трубах ламинарный режим течения наблюдается до

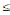
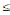 2,3
2,3 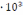

103, переходной режим течения имеет место при 2,3

 103
103 

 104 и турбулентный режим течения устанавливается при
104 и турбулентный режим течения устанавливается при 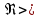 104.
104.Число Прандтля характеризует соотношение молекулярных свойств переноса количества движения и теплоты и определяется по формуле
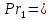
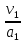 , (1.7)
, (1.7)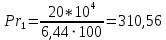

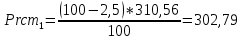
где
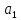 – коэффициент температуропроводности жидкости, м2/с. Значения коэффициента температуропроводности и число Прандтля приведены в табл. 2.
– коэффициент температуропроводности жидкости, м2/с. Значения коэффициента температуропроводности и число Прандтля приведены в табл. 2.Число Грасгофа характеризует отношение подъемной силы, возникающей вследствие теплового расширения, к силам вязкости и определяется по формуле
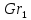

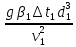 , (1.8)
, (1.8) 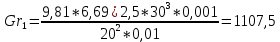
гдеg = 9,81м/с2 – ускорение свободного падения;
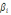
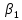 – температурный коэффициент объемного расширения жидкости, 1/К, (значения
– температурный коэффициент объемного расширения жидкости, 1/К, (значения 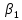 для жидкостей приведены в табл. 2);
для жидкостей приведены в табл. 2); 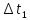 =
= 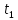 –
–