МИНИСТЕРСТВО НАУКИ ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный нефтяной технический университет» (ФГБОУ ВО УГНТУ)

Институт нефтепереработки и нефтехимии ФГБОУ ВО УГНТУ в г. Салавате
Кафедра «Информационных технологий»

Физика
ИЗУЧЕНИЕ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ ТЕЛ

С ПОМОЩЬЮ ШТАНГЕЦИРКУЛЯ И МИКРОМЕТРА
Отчет по лабораторной работе № 1
ИнТех- 18.03.02 –1.01.01 ЛР

Исполнитель:

студент гр. БМОз- 22-21 В.А.Медведев

Руководитель:

ассистент Г.Ф. Шаяхметов

Салават

2023

Цель работы: Измерение геометрических размеров тел с помощью штангенциркуля и микрометра, определение их объемов.

Приборы и принадлежности: штангенциркуль, стальная пластинка,

стальной цилиндр, микрометр.
Теоретическая часть

1. Линейный нониус. Штангенциркуль.

Линейные величины измеряют с помощью различных приборов и инструментов. Наибольшее распространение получили следующие из них: масштабная линейка, микрометр, микроскоп и др. Каждый, из этих приборов, допускает измерения с определенной точностью.

Пусть измерения проводятся с помощью масштабной линейки. Величина наименьшего деления линейки называется ценой одного деления. Обычно цена деления линейки составляет

1 мм. Точность с которой можно измерить, используя такую линейку не превышает 0,5 мм.

Для измерения длины с большей точностью пользуются дополнительной специальной шкалой – нониусом.

Нониусы бывают линейные и угловые. Линейным пользуются при измерении линейных величин, а угловым при измерении угловых величин.

---

Линейный нониус представляет собой небольшую линейку, скользящую вдоль основной шкалы (рис. 1)



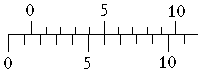
Рисунок 1 - Линейный нониус.
Пусть на нониус нанесена шкала, N делений которой равны rN-1 делениям основной шкалы, где rN – целое число.

Если “а” цена деления (длина одного деления) нониуса, а “b” цена деления основной шкалы, то можно записать следующее выражение:
Na = (rN – 1) b (1).

Разность

rb – a = b/N (2).

получаемая из формулы (1) называется точностью нониуса, т.е. точность нониуса – отношение цены наименьшего деления основной шкалы к числу делений нониуса. Точность нониуса бывает 0,2 мм; 0,1 мм; 0,05 мм.

Процесс измерения длины при помощи нониуса сводится к следующему. Совмещают нулевое деление шкалы линейки А с одним концом измеряемого тела В, к другому концу прикладывается нониус С (рис. 2). Измеряемая длина тела В
L = kb + L (3)
где: k – целое число делений масштабной линейки, в измеряемой длине;

L – отрезок длины, представляющий доли миллиметра, который необходимо определить.

Если n делений нониуса, которое совпадает с любым каким-то делением шкалы линейки А, то (для r=1):
L = nb – na = n (b – a) = nb/N (4)
Формулу (3) после этого можно записать в виде:
L = kb + nb/N (5)

Если положить b = 1мм, N = 10 делений, то искомая длина:
L = (k + n/10) b мм (6)
Выражение (6) показывает, что длина измеряемого тела равна целому числу k мм масштабной линейки плюс десятые доли числа n:

Число n показывает тот номер деления нониуса, который совпадает с некоторым делением масштабной линейки.

На рис. 1 приведен пример отсчета длины

L = (14 + 5/10) = 14?5

так как k = 14мм, n = 5.
Линейный нониус применен в инструменте, который называется штангенциркулем.


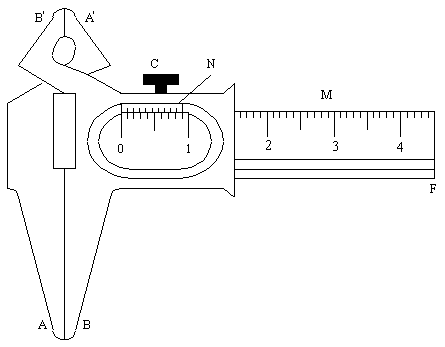
Рисунок 2 - Штангенциркуль.

Штангенциркуль (рис. 2) служит для измерения линейных величин. Он состоит из стальной линейки М с делениями, с одной стороны которой имеется неподвижная ножка А. Цена деления шкалы линейки М равна обычно 1 мм. Вторая ножка В имеет нониус N и может перемещаться вдоль шкалы линейки.

Нониус штангенциркулей изготавливается так, чтобы r= 1,2 и 5 (см. формулу (1).) Точность нониуса обычно равна 0,1; 0,05; или 0,2. Когда ножки А и В соприкасаются, нуль нониуса и нуль основной шкалы должны совпадать.

---

Для того, чтобы измерить, например, диаметр предмета , его зажимают между ножками (без сильного зажима), закрепляют винтом С и делают отсчет по основной шкале и нониусу. Величину диаметра надо вычислить по формуле (6).
2. Микрометрический винт. Микрометр.

Микрометрический винт применяется в инструментах и приборах следующих типов: микрометр для наружных измерений, микрометрический глубиномер, микрометрический нутромер, микроскоп и др. Позволяет проводить измерения с точностью до сотых долей миллиметра.

Микрометрический винт представляет собой стержень, снабженный точной винтовой нарезкой. Высота подъема винтовой нарезки за один оборот называется шагом микрометрического винта.

В настоящей работе используется микрометр для наружных измерений (рис. 3). Он состоит из скобы L и микрометрического винта D, который проходит через отверстие скобы, в котором имеется внутренняя резьба. Против торца винта В, на скобе установлен неподвижный стержень А. На микрометрическом винте закреплен барабан С с делениями нанесенными по окружности. При вращении винта барабан, кроме вращательного движения участвует в поступательном движении вдоль шкалы нанесенной на стебле D. Цена деления этой шкалы 0,5 мм. Так как шаг винта составляет 0,5 мм нужно сделать один оборот. Круговая шкала барабана разделена на 50 делений. Цена делений этой шкалы составляет 0,01.

Для измерения микрометром предмет располагают между стержнем А и стержнем В и вращают винт за головку Е до тех пор, пока измеряемый предмет не будет зажат. В этот момент заработает трещотка. Вращать винт В следует только за головку Е. В противном случае испортиться микрометр.







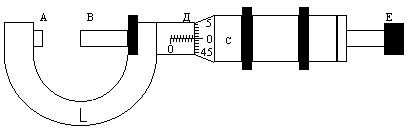
Рисунок 3 - Микрометр.
Отсчет по шкале микрометра производится следующим образом: по горизонтальной шкале стебля D отсчитывается размер измеряемого предмета с точностью до 0,5 мм. Сотые доли миллиметра отсчитываются по круговой шкале барабана С (рис. 3).

Результат измерения находят по формуле:

L=kb+nb/N (1)

Где: k – целое число наименьших делений шкалы нанесенной на стебле D, b – цена деления этой шкалы, N – число делений на шкале барабана, n – номер того деления барабана, которое располагается против продольной черты на стебле D. Порядок отсчета одинаков для всех микрометрических инструментов. Микрометры бывают с пределами измерения 0 – 25, 50, 75 мм и т.д. до 1600 мм.

---

Увеличение пределов достигается за счет увеличения размеров скобы В.

Порядок выполнения работы
Задание №1
1.1 Измерить длину пластинки с помощью штангенциркуля в нескольких местах для этого пластину зажать между лапками А и В (проделать 4-8 раз в зависимости от разброса результатов).

1.2 Измерить ширину и толщину пластинки так как указано в п.1.

1.3 Результаты занести в таблицу 1.

1.4 Вычислить полные абсолютные погрешности а, b, с и относительные погрешности этих же величин:

1.5 Вычислить V по формуле

1.6 Вывести формулы для расчета Е_V и V, вычислить их.

1.7 Записать гарантированное значение объема в виде: V=V  V
Задание №2
2.1 С помощью микрометра цилиндр нужно зажать между торцами стержней А и В, вращая микровинт за головку Е. Размеры предметов определить по формуле (1).

2.2 Измерение диаметра и высоты цилиндра повторить 4-8 раз в различных местах.

2.3 Результаты занести в таблицу 2:

3. 
   Провести обработку результатов измерений и записать гарантированные значения измеряемых величин, как при измерении штангенциркулем.
   

Расчетная часть
Задание №1

1. 
   Измерил длину пластинки с помощью штангенциркуля в нескольких местах для этого пластину зажал между лапками А и В.
   

Измеряемая длина стальной пластинки:

L = kb + L

k – целое число делений масштабной линейки, в измеряемой длине (k=49);

L – отрезок длины, представляющий доли миллиметра, который необходимо определить.

L = nb – na = n (b – a) = nb/N,

n - номер деления нониуса, который совпадает с некоторым делением масштабной линейки (n=18).

L = kb + nb/N=49·1+18·1/20=49, 9(мм).
а=49,9; 49,9; 49,8; 49,75; 49,85; 49,9 мм

2. 
   Измерил ширину и толщину пластинки так как указано в п.1.
   

b=33,9; 33,8; 33,8; 33,9; 33,8; 33,9 мм

c=8,6; 8,6; 8,6; 8,6; 8,6; 8,6 мм

3. 
   Результаты занести в таблицу 1.
   

Результаты измерения (в мм) пластины штангенциркулем (цена деления линейки b=1; цена деления нониуса а= 0,95; точность b/N=0,05; r=1.
Таблица 1.

№	длина а	а	Ширина B	<b>	Толщина С	<С>	Примеч.
1. 2. 3. 4. 5. 6.	49,9 49,9 49,8 49,75 49,85 49,9	0,08	33,9 33,8 33,8 33,9 33,8 33,9	0,08	8,6 8,6 8,6 8,6 8,6 8,6	0,1
Сред	49,85		33,85		8,6

---

b=1-цена деления основной шкалы, r=1, N=20-число делений на шкале нониуса.

Na=(rN-1)b, отсюда цена деления равна:



Точность нониуса

b/N=rb-a=1*1-0,95=0,05

Средние значения длины, ширины, толщины:







1.4 Вычислил полные абсолютные погрешности а, b, с и относительные погрешности этих же величин:



;

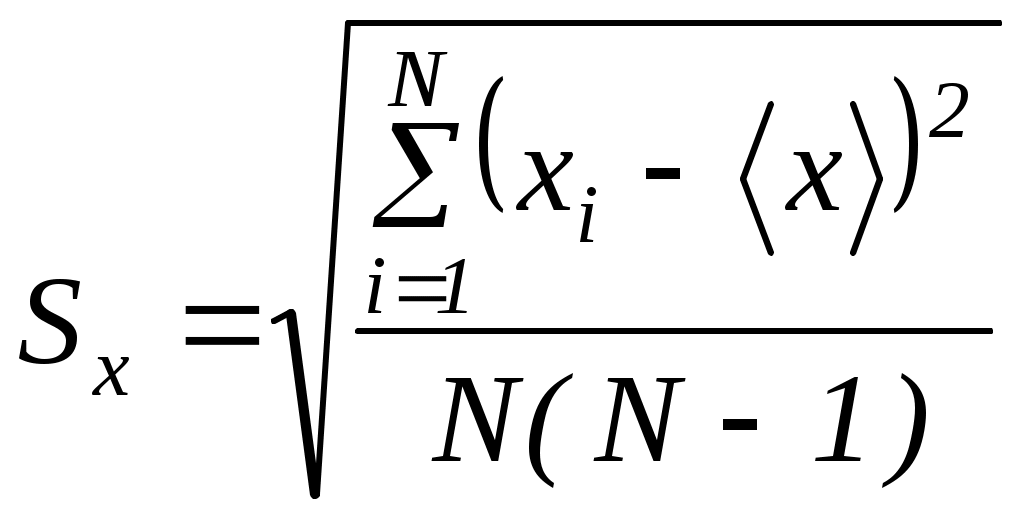х_сл = S_xt(, N);

,

где t(, N) - коэффициент Стьюдента, t(α,N)=0,95;

S_x – стандартное отклонение,

х_сл - случайная ошибка,

Х-полная абсолютная погрешность, α=0,6;

N=6 – число измерений.



≈0,03
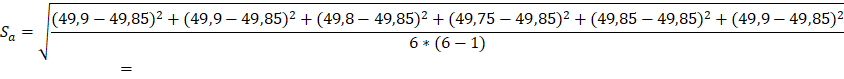
a_сл=2,58*10^-2*0,95=2,451*10^-2≈0,02

a= ≈0,08



a=±a=(49,85±0,08)мм




≈0,02
b_сл=2,236*10^-2 *0,95=2,124*10^-2≈0,02

b= ≈0,08



b=±b=(33,85±0,08)мм



c_сл=0 *0,95=0

c= ≈0,1



c=±c=(8,6±0,1)мм

4. 
   Вычислил V по формуле
   

=49,85*33,85*8,6=14511,8 мм³

5. 
   Вывел формулы для расчета Е_V и V, вычислил их.
   

E_v=E_a+E_b+E_c;

E_v=(1,58+2,3+8,72)*10^-3=1,3*10^-2≈0,01

6. 
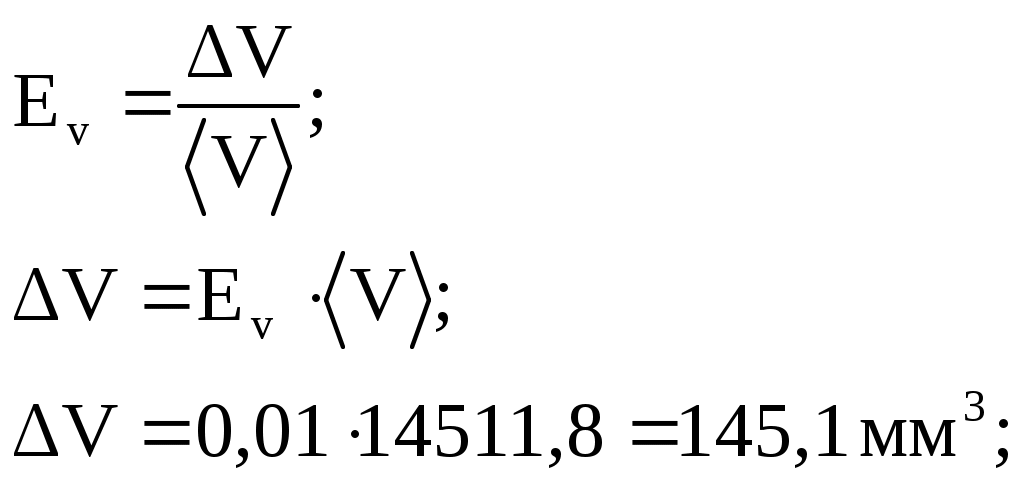
   Записал гарантированное значение объема в виде: V=V  V
   

V=(14511,8±145,1) мм³

Задание №2
2.1 С помощью микрометра цилиндр зажал между торцами стержней А и В, вращая микровинт за головку Е. Размеры предметов определил по формуле L=kb+nb/N.

Где: k – целое число наименьших делений шкалы нанесенной на стебле D (k=36), b – цена деления этой шкалы (b=0.5), N – число делений на шкале барабана (N=50), n – номер того деления барабана, которое располагается против продольной черты на стебле D (n=10).

L=36*0,5+10*0,5/50=18,1 мм

2.2 Измерение диаметра и высоты цилиндра повторил 6 раз в различных местах.

d=18,1; 18,1; 18,1; 18,1; 18,1; 18,1 мм

C=18,1; 18,1; 18,1; 18,1; 18,1; 18,1 мм

2.3 Результаты занести в таблицу 2:

Таблица 2.

Результаты измерения (в мм) цилиндра микрометром (цена деления шкалы барабана b=0,01 мм; число делений на барабане N=50;)

№	d	d	Ed	C	C	Ec	Примеч.
1. 2. 3. 4. 5. 6.	18,1 18,1 18,1 18,1 18,1 18,1		0	18,1 18,1 18,1 18,1 18,1 18,1		0
Сред	18,1			18,1

= мм

= мм

3. 
   Провел обработку результатов измерений и записал гарантированные значения измеряемых величин, как при измерении штангенциркулем.
   

;

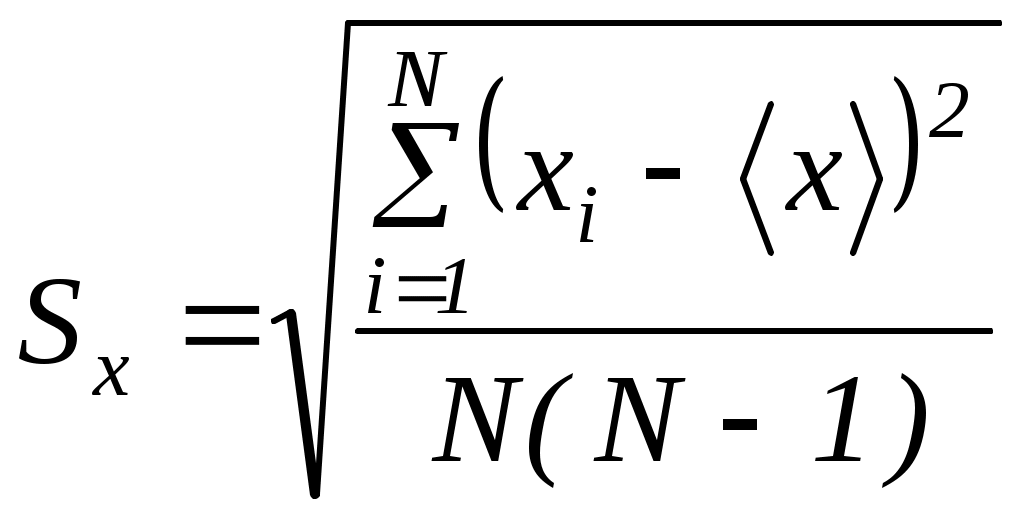х_сл = S_xt(, N);

,

где t(, N) - коэффициент Стьюдента, t(α,N)=0,95;

S_x – стандартное отклонение,

х_сл - случайная ошибка,

Х-полная абсолютная погрешность, α=0,6;

N=6 – число измерений.



b_сл=0*0,95=0

b= ≈0,1




C_сл=0*0,95=0

C= ≈0,1



Гарантированные значения диаметра и высоты цилиндра.

b=±b=(18,1±0,1)мм

C=±C=(18,1±0,1) мм

Вывод:

В ходе выполнения работы, используя штангенциркуль, я определил размеры пластины, обработал результаты измерений, вычислил её объём, учитывая при этом погрешности. Длина пластины составила: a = (39,74 ±0,14)мм, ширина составила: b = (24,46 ±0,17)мм, толщина составила: c = (7,28 ±0,17)мм.

Объём пластинки составил: .

Во втором опыте был применен микрометр. Я измерил диаметр и высоту цилиндра. Подсчитал все погрешности.

Диаметр цилиндра составил: высота цилиндра: C=( ) мм. Объем цилиндра составил: V = (4960,7 ± 192,5) мм³

---

Смотрите также файлы

• В наши дни, в благоуханье цветущих яблонь, погибла моя роща где спрятаться от летней жары.docx

• Министерство науки высшего образования российской федерации.doc

• абит мсірепов авгейді ат орасынан бастайы Бдан былай огурци деп жазылатын болса, мен оны жемейа оярмын.docx

• Задача по дисциплине Философия. Мустафаева Д. Б. Проверил Кузин И. В санкт Петербург спбутуиЭ 2023 Задвние 1.docx

• псковский государственный университет.docx