Файл: Контрольная работа вариант 2 по дисциплине Эконометрика Исполнитель студент гр.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Линейный коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Его можно определить по следующей формуле:
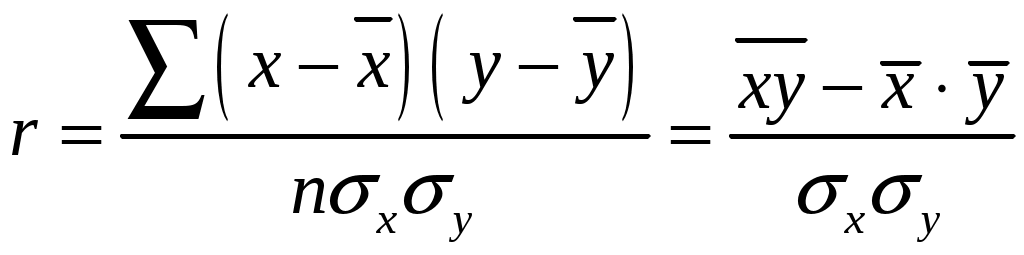 ,
,где
Вычислим :
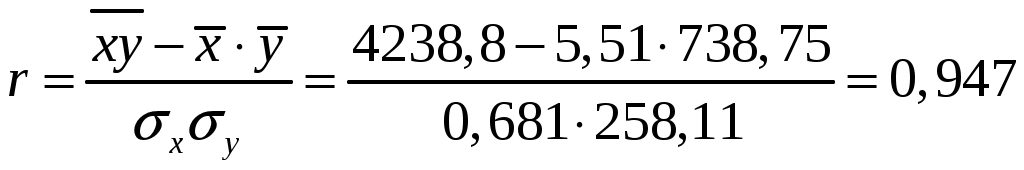
Значения линейного коэффициента корреляции принадлежит промежутку [-1;1]. Связь между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
менее 0,1 отсутствует линейная связь
0,1 < rxy < 0,3: слабая;
0,3 < rxy < 0,5: умеренная;
0,5 < rxy < 0,7: заметная;
0,7 < rxy < 0,9: высокая;
0,9 < rxy < 1: весьма высокая;
Для нашей задачи r = 0,947, что подтверждает вывод, сделанный ранее, что связь между признаками прямая, а также указывает на весьма высокую взаимосвязь между чистой прибылью и числом оборотов оборотных средств. Положительная величина свидетельствует о прямой связи между изучаемыми признаками, т.е. с ростом числа оборотов оборотных средств, растет и чистая прибыль.
-
Рассчитать стандартизованные - коэффициенты и пояснить их экономический смысл:
- коэффициенты и пояснить их экономический смысл:
Стандартизированный коэффициент связаны с коэффициентом обычного уравнения регрессии соотношениями
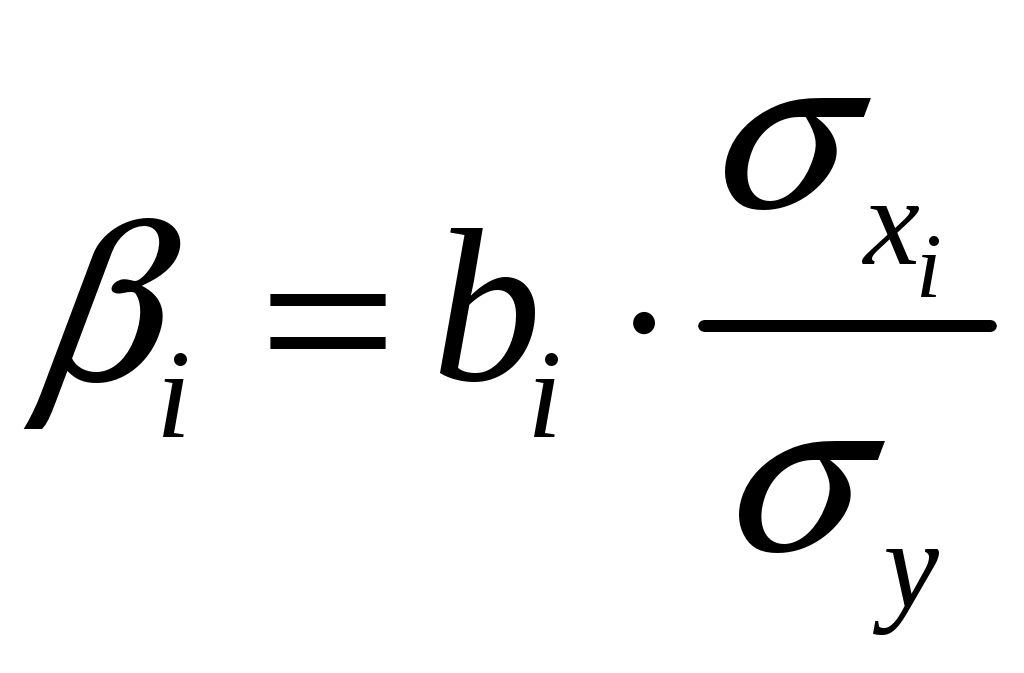
Следовательно,
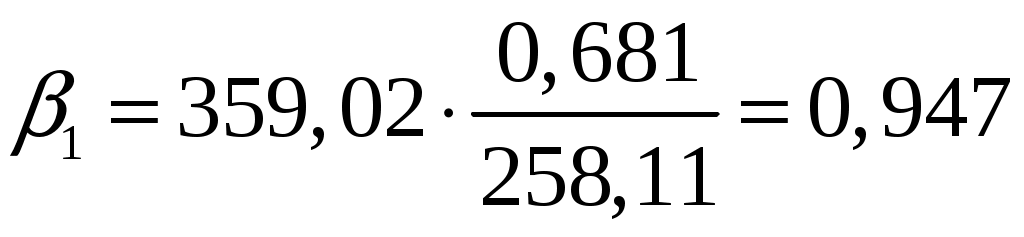
Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднеквадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированных на постоянном уровне значениях остальных независимых переменных. Это означает, что при увеличении числа оборотов оборотных средств на 0,681 чистая прибыль увеличится на 0,947.
-
Рассчитаем коэффициент детерминации, эластичности и поясним их экономический смысл:
Коэффициент детерминации определяется по формуле:
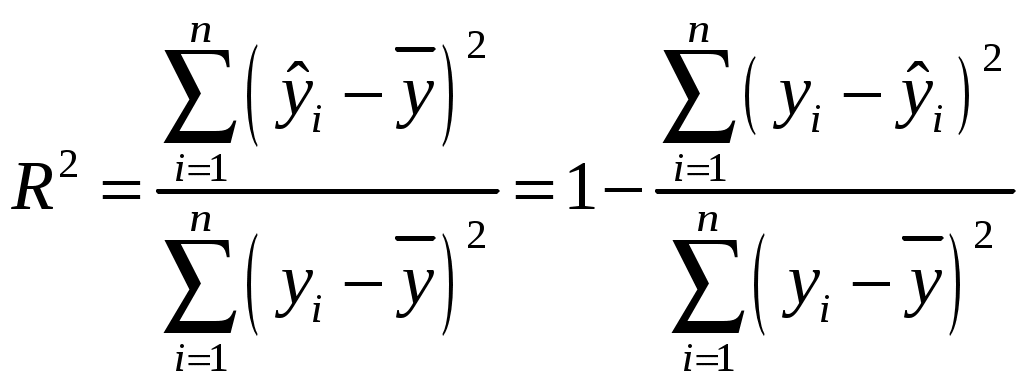
Вычислим:
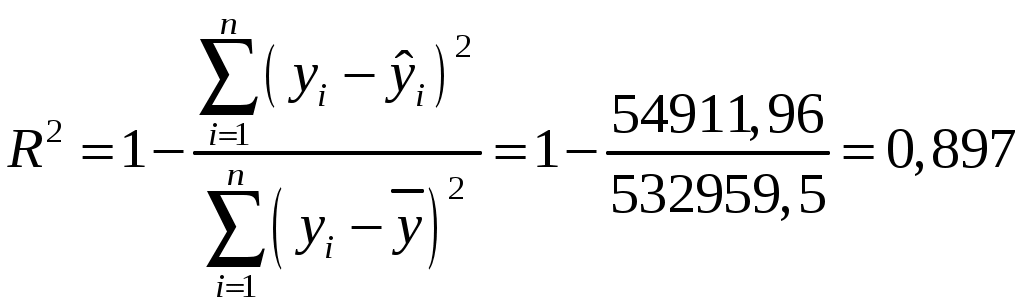
Множественный коэффициент детерминации
Коэффициент эластичности рассчитываем по формуле:
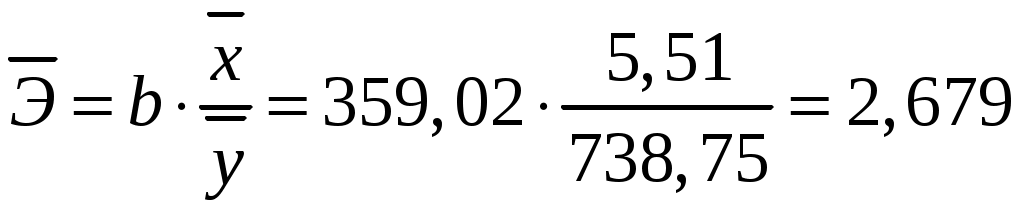
Увеличение числа оборотов оборотных средств (от своего среднего значения) на 1% увеличивает в среднем чистую прибыль на 2,68%.
-
Рассчитаем ошибку аппроксимации и дадим характеристику её величины:
Средняя ошибка аппроксимации по формуле:
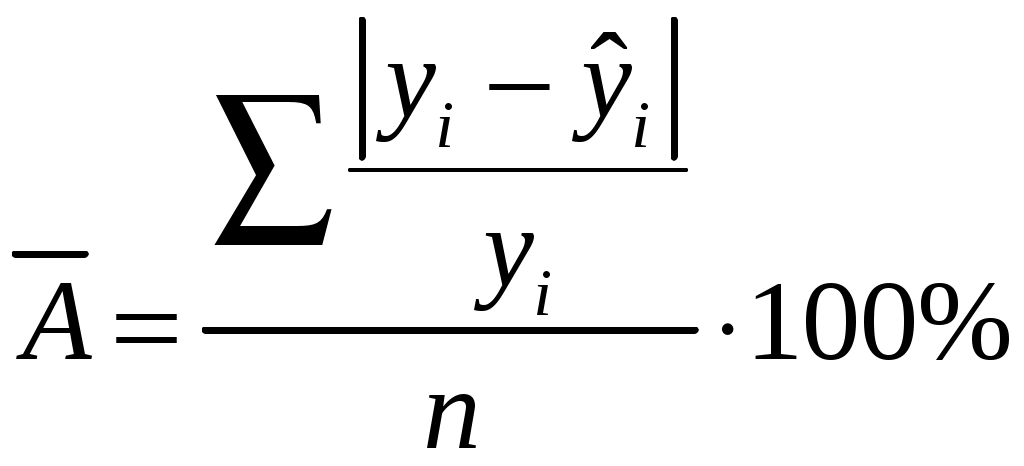
Найдем величину средней ошибки аппроксимации
В среднем, расчетные значения отклоняются от фактических на 9,90% поскольку ошибка меньше 10%, то качество модели хорошее и данное уравнение можно использовать в качестве регрессии.
-
Оценим достоверность модели по критерию Фишера:
Оценку статистической значимости уравнения регрессии в целом
проведем с помощью
критерия по формуле составит
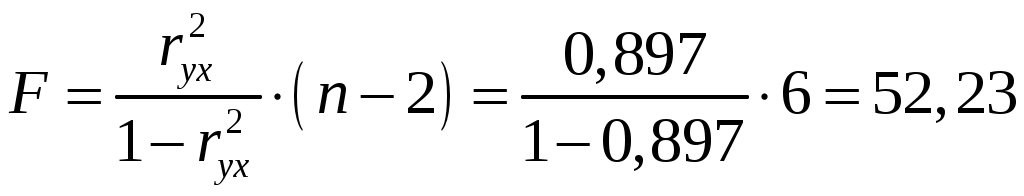
Для определения табличного значения F-критерия при доверительной вероятности 0,05 и при
Табличное значение критерия при пятипроцентном уровне
значимости и степенях свободы
-
На основании полученных моделей рассчитать ожидаемое в среднем по предприятиям значение показателя эффективности деятельности при ожидаемых значениях факторов, приведенных в таблице исходных данных:
Прогнозное значение числа оборотов оборотных средств:
Прогнозное значение чистой прибыли:
Для расчета точечного прогноза
где tтабл - табличное значение t-критерия Стьюдента для уровня значимости
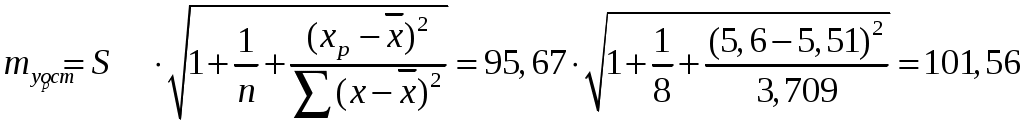
Предельная ошибка прогноза, которая в
Доверительный интервал прогноза:
Выполненный прогноз чистой прибыли является надежным (
Задача 2
Таблица – Исходные данные
| № предприятия | Затраты на 1 руб. продукции, руб. | Число оборотов оборотных средств, раз | Чистая прибыль, тыс. руб. |
| | Х1 | Х3 | У |
| 1 | 96 | 4,0 | 220 |
| 2 | 52 | 6,2 | 1070 |
| 3 | 60 | 6,1 | 1000 |
| 4 | 89 | 5,4 | 606 |
| 5 | 82 | 5,8 | 780 |
| 6 | 77 | 6,0 | 790 |
| 7 | 70 | 5,6 | 900 |
| 8 | 92 | 5,0 | 544 |
| | Средние ожидаемые значения показателей (план) | | |
| | 80 | 5,6 | |
По статической информации, представленной в таблице исходных данных в задаче 1 исследовать зависимость результативного показателя (Y) от факторов (Х1, Х2, Х3, Х4, Х5):
1. С помощью EXCEL провести регрессионный анализ зависимости результативного показателя от факторных признаков.
2. Построить модель множественной регрессии.
3. Дать экономическую характеристику коэффициентов множественной регрессии, корреляции и детерминации.
4. Оценить достоверность модели по критерию Фишера и по критерию Стьюдента.
5. На основании полученных моделей рассчитать ожидаемое в среднем по предприятиям значение показателя эффективности деятельности при ожидаемых значениях факторов, приведенных в таблице исходных данных.
Решение:
1. С помощью EXCEL провести регрессионный анализ зависимости результативного показателя от факторных признаков:
Для построения корреляционного анализа воспользуемся пакетом прикладных программ Microsoft Excel, функцией «Анализ данных».
Выполняем следующие действия:
-
Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек. -
Выбрать команду «Сервис» → «Анализ данных». -
В диалоговом окне «Анализ данных» выбрать инструмент «Корреляция», а затем щелкнуть кнопку «ОК». -
В диалоговом окне «Корреляция» в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если введены и заголовки столбцов, то установить флажок «Метки в первой строке». -
Выбрать параметры вывода. В данном случае «Новый рабочий лист». -
«ОК»
Таблица 1
Результаты корреляционного анализа
| | y | x1 | x3 |
| y | 1 | | |
| x1 | -0,92598 | 1 | |
| x3 | 0,947084 | -0,80346 | 1 |
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т. е. чистая прибыль, имеет тесную и прямую связь с числом оборотов оборотных средств (
Затем перейдем к анализу остальных столбцов матрицы с целью выявления коллинеарности. Связь между факторами не обладает коллинеарностью.
Таким образом, на основе анализа только корреляционной матрицы остаются оба фактора - Затраты на 1 руб. продукции (Х1) и Число оборотов оборотных средств (Х3) (n =8, m=2).
2. Построим модель множественной регрессии:
Получим уравнение регрессии, используя инструмента Регрессия в Анализе данных (таб.1).
Таблица 1. Результаты работы с инструментом Регрессия
| ВЫВОД ИТОГОВ | | | | | | |
| | | | | | | |
| Регрессионная статистика | | | | | | |
| Множественный R | 0,986819 | | | | | |
| R-квадрат | 0,973812 | | | | | |
| Нормированный R-квадрат | 0,963336 | | | | | |
| Стандартная ошибка | 52,83428 | | | | | |
| Наблюдения | 8 | | | | | |
| | | | | | | |
| Дисперсионный анализ | | | | | | |
| | df | SS | MS | F | Значимость F | |
| Регрессия | 2 | 519002,2 | 259501,1 | 92,96245 | 0,000111 | |
| Остаток | 5 | 13957,31 | 2791,461 | | | |
| Итого | 7 | 532959,5 | | | | |
| | | | | | | |
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95,0% |
| Y-пересечение | 175,0142 | 399,7057 | 0,437858 | 0,679758 | -852,462 | 1202,49 |
| x1 | -8,20212 | 2,141364 | -3,83033 | 0,012244 | -13,7067 | -2,69757 |
| x3 | 217,2063 | 46,08134 | 4,713542 | 0,005273 | 98,75046 | 335,6621 |
| | | | | | | |
| ВЫВОД ОСТАТКА | | | | | | |
| | | | | | | |
| Наблюдение | Предсказанное y | Остатки | | | | |
| 1 | 256,4357 | -36,4357 | | | | |
| 2 | 1095,183 | -25,1829 | | | | |
| 3 | 1007,845 | -7,84532 | | | | |
| 4 | 617,9393 | -11,9393 | | | | |
| 5 | 762,2367 | 17,76327 | | | | |
| 6 | 846,6886 | -56,6886 | | | | |
| 7 | 817,2209 | 82,77906 | | | | |
| 8 | 506,4505 | 37,54954 | | | | |
Уравнение зависимости чистой прибыли от затрат на 1 руб. продукции и числа оборотов оборотных средств можно записать в следующем виде: ŷ= 175,014 – 8,202∙x1 +217,206∙х3
3. Дадим экономическую характеристику коэффициентов множественной регрессии, корреляции и детерминации:
В этом уравнении величина, равная –8,202 (коэффициент при х1), показывает, что при увеличении затрат на 1 руб. продукции на 1 руб. при неизменном обороте оборотных средств, чистая прибыль снизится в среднем на 8,202 тыс. руб., а если на 1 раз увеличится число оборотов оборотных средств, при тех же затратах на 1 руб. продукции, чистая прибыль увеличится на 217,206 тыс. руб.
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения, или из последней таблицы регрессионного анализа Вывод остатка (столбец Предсказанное Y).
Значение коэффициентов детерминации и множественной корреляции можно найти в таблице Регрессионная статистика (см. таб.1) или вычислить по формулам:
а) коэффициент детерминации: R2 = 0,974
Коэффициент детерминации показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 97,4% вариации чистой прибыли объясняется учтенными в модели факторами: затраты на 1 руб. продукции и число оборотов оборотных средств.
б) коэффициент множественной корреляции: R = 0,987.
Коэффициент множественной корреляции показывает весьма высокую тесноту связи зависимой переменной Y с двумя включенными в модель объясняющими факторами.
4. Оценим достоверность модели по критерию Фишера и по критерию Стьюдента.
Проверку значимости уравнения регрессии произведем на основе F- критерия Фишера: Fфакт=92,962.
Значение F-критерия Фишера можно найти в таблице Дисперсионный анализ протокола Excel (таб.1).
Табличное значение F-критерия при доверительной вероятности α = 0,95 и числе степеней свободы, равном
k1=m = 2 и k2 = n - m - 1= 8 - 2 - 1 = 5 составляет 5,79. Для этого можно воспользоваться статистической функцией FРАСПОБР.
Поскольку Fфакт > Fтабл, то уравнение регрессии следует признать значимым, то есть его можно использовать для анализа и прогнозирования.
Оценку значимости коэффициентов полученной модели, используя результаты отчета Excel, можно осуществить тремя способами.
Коэффициент уравнения регрессии признается значимым в том случае, если:
-
наблюдаемое значение t-статистики Стьюдента для этого коэффициента больше, чем критическое (табличное) значение статистики Стьюдента (для заданного уровня значимости, например, α = 0,05 и числа степеней свободы df = n - m - 1, где n - число наблюдений, а m - число факторов в модели);
-
P-значение t-статистики Стьюдента для этого коэффициента меньше, чем уровень значимости, например, α= 0,05;
-
доверительный интервал для этого коэффициента, вычисленный с некоторой доверительной вероятностью (например, 95%), не содержит ноль внутри себя, то есть если нижняя 95% и верхняя 95% границы доверительного интервала имеют одинаковые знаки.
Значимость коэффициентов регрессии оценим с помощью
В результате выполнения регрессионного анализа в пакете Excel получены оценки а и bi и их Р – значения:
Коэффициенты t-статистика Р-значение
а 175,014 0,44 0,68
b1 –8,202 – 3,83 0,01
b2 217,206 4,72 0,01
Для коэффициента а вероятность его не влияния на у равна 0,68 (68%), что больше порогового значения в 5%, поэтому коэффициент а признается не значимым и должен быть удален из модели.
Для коэффициента b1 вероятность его не влияния на у