Файл: Контрольная работа вариант 2 по дисциплине Эконометрика Исполнитель студент гр.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
равна 0,01 (1%), что меньше порогового значения в 5%, поэтому коэффициент b1 признается значимым и оставляется в модели.
Для коэффициента b2 вероятность его не влияния на у равна 0,01 (1%), что меньше порогового значения в 5%, поэтому коэффициент b1 признается значимым и оставляется в модели.
Расчетные значения критерия Стьюдента следующие:;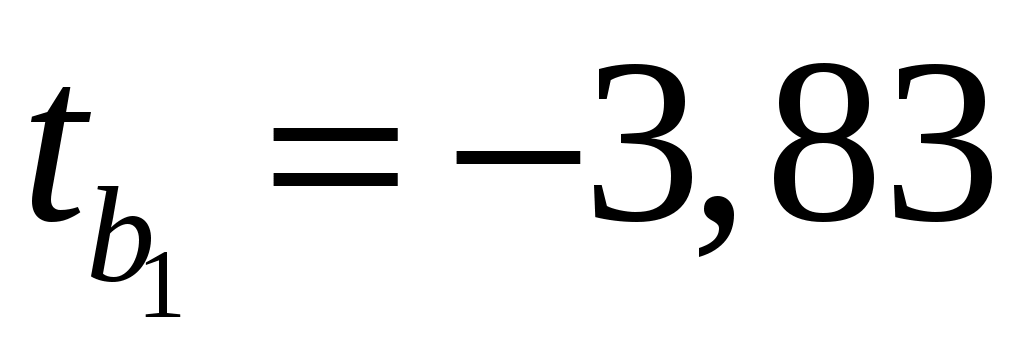 и . Табличное значение критерия при уровне значимости
и . Табличное значение критерия при уровне значимости 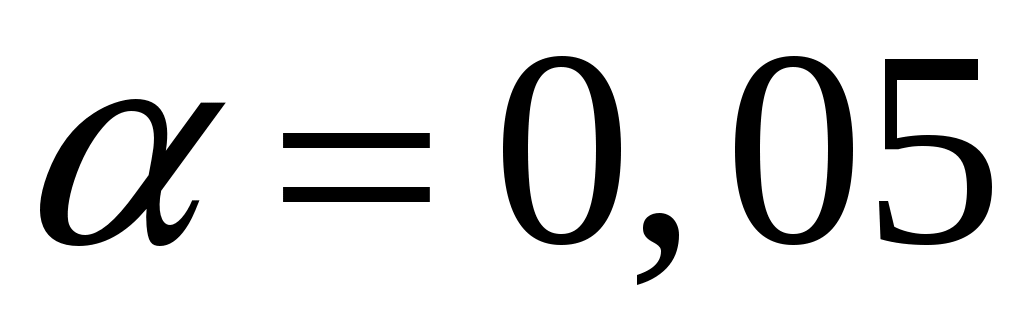 и числе степеней свободы
и числе степеней свободы 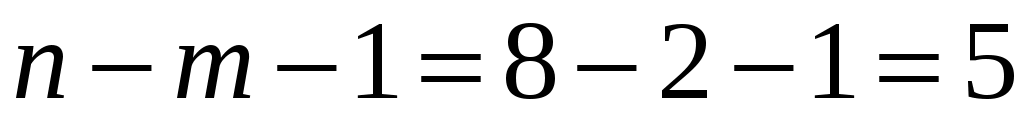 равно 2,57.
равно 2,57.
Таким образом, признается статистическая значимость параметров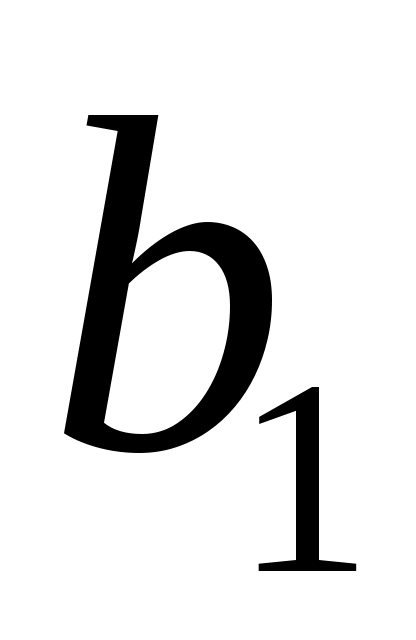 и
и 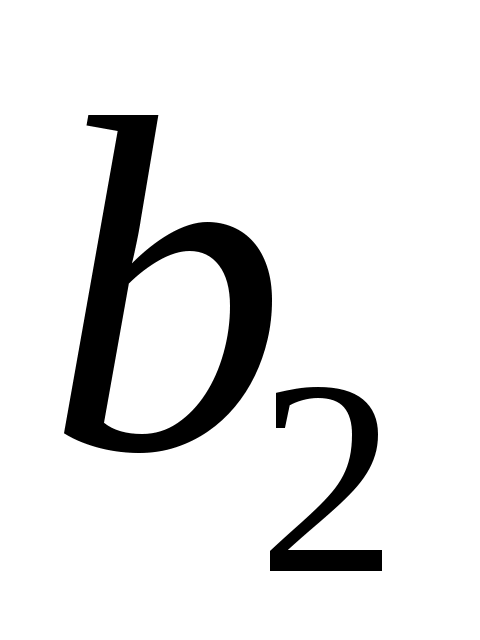 , т.к.
, т.к. 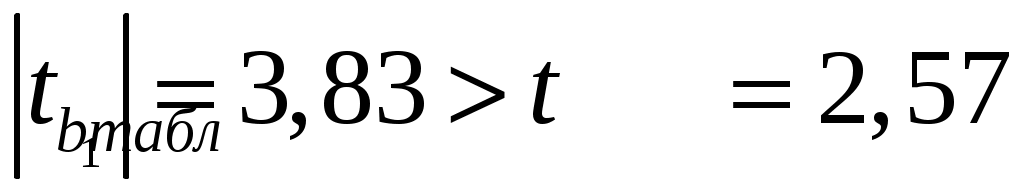 и
и 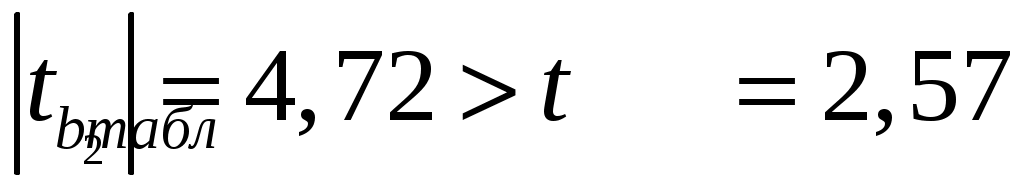 , и признается статистическая не значимость параметра
, и признается статистическая не значимость параметра 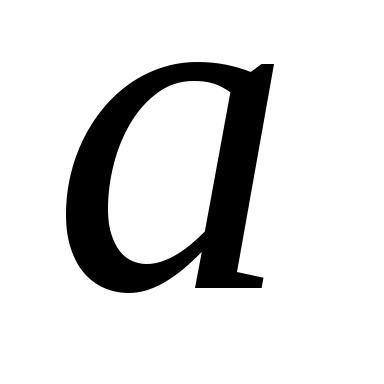 , т.к.
, т.к. 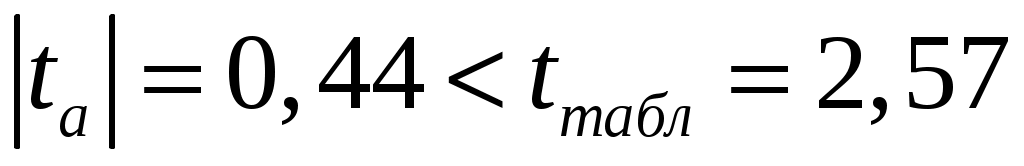 .
.
Прогнозное значение затрат на 1 руб. продукции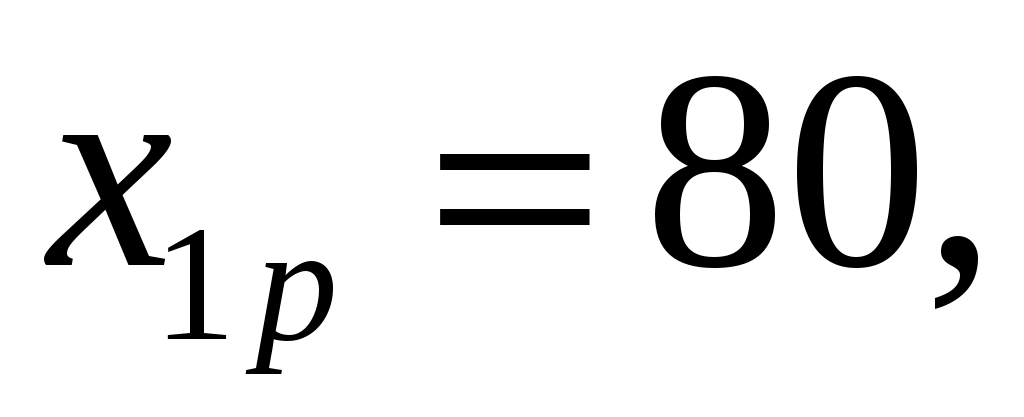 чел/100 т.руб и числа оборотов оборотных средств:
чел/100 т.руб и числа оборотов оборотных средств: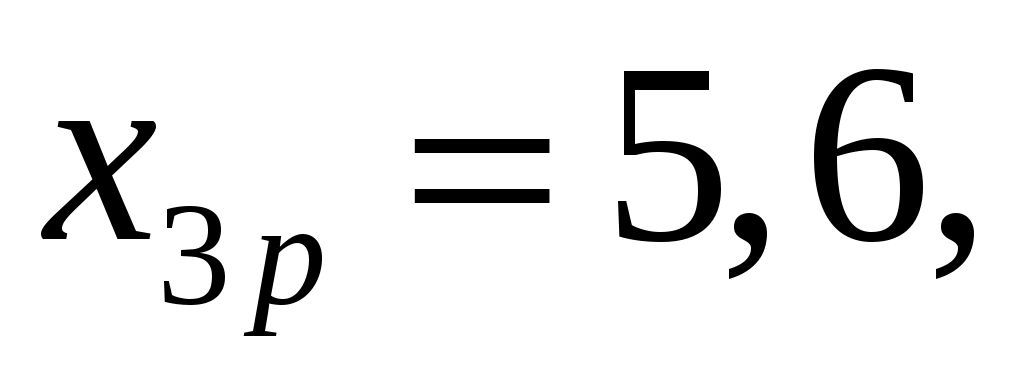 раз
раз
Прогнозное значение чистой прибыли:
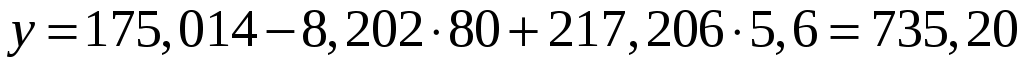 тыс. руб.
тыс. руб.
Задача 3
Провести анализ динамики курса доллара в течение года (приложение) по своему варианту:
1. Провести выравнивание временного ряда методом скользящей средней.
2. Рассчитать сезонную компоненту S и устранить её из исходных членов ряда и получение выровненных данных.
Решение:
Исходные данные для анализа представлены в таблице:
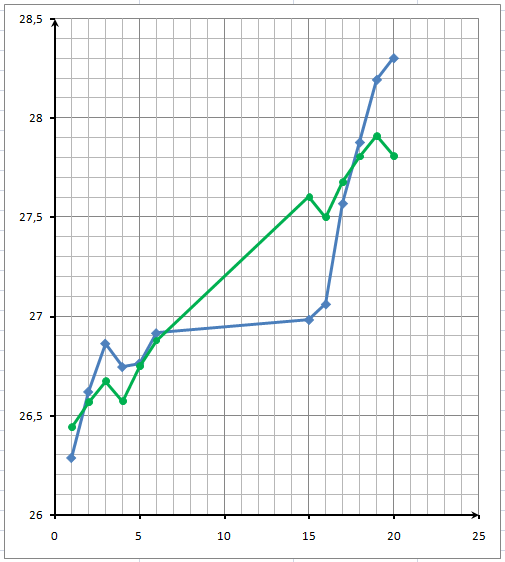
Исходная динамика курса доллара представлена на рис. 1.
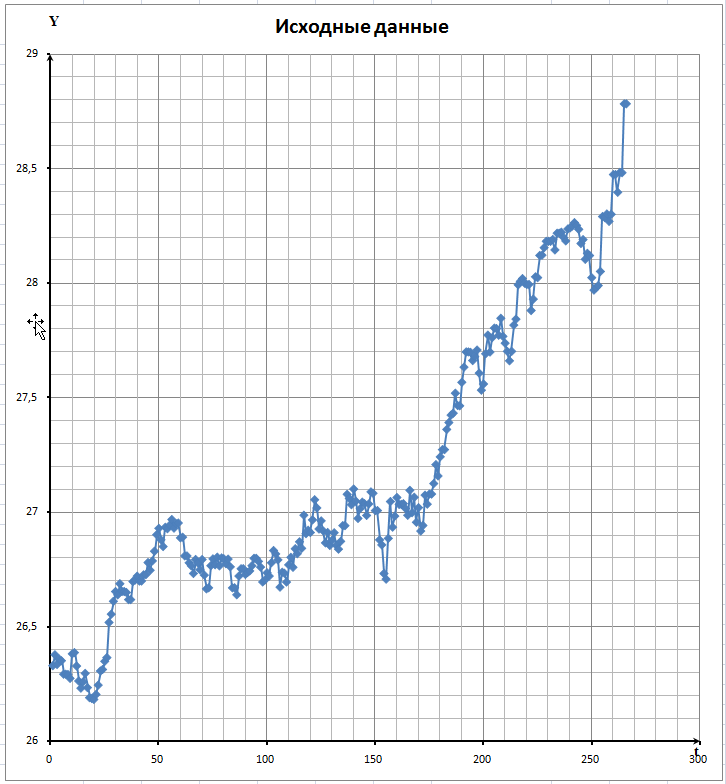
рис. 1
Укрупним интервал, рассчитав среднемесячный курс валюты
1. Проведем выравнивание временного ряда методом скользящей средней:
Найдем скользящие средние. Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.
2. Рассчитать сезонную компоненту S и устранить её из исходных членов ряда и получение выровненных данных.
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние за каждый период оценки сезонной компоненты Sj. Сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Рассчитываем скорректированные значения сезонной компоненты Si и заносим полученные данные в таблицу. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y - S. Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда.
Для определения параметров уравнения и
и 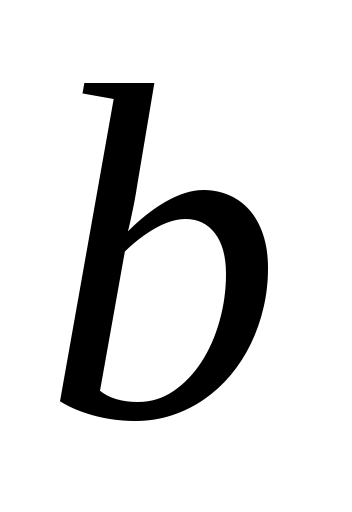 составим систему нормальных уравнений. Исходное уравнение последовательно умножим на коэффициенты при неизвестных
составим систему нормальных уравнений. Исходное уравнение последовательно умножим на коэффициенты при неизвестных  и
и 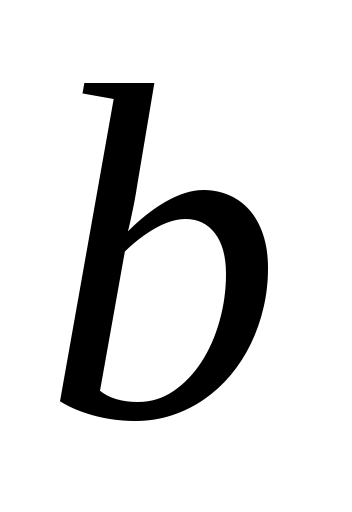 , и затем каждое уравнение просуммируем:
, и затем каждое уравнение просуммируем:
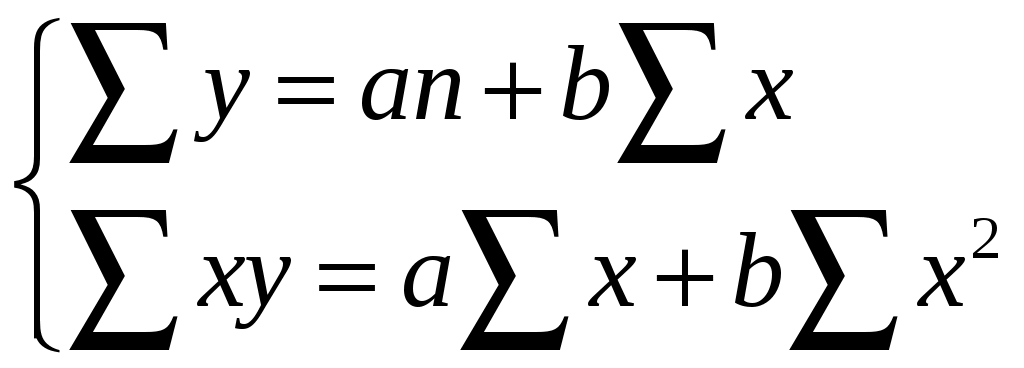
Подставим полученные данные в систему уравнений:
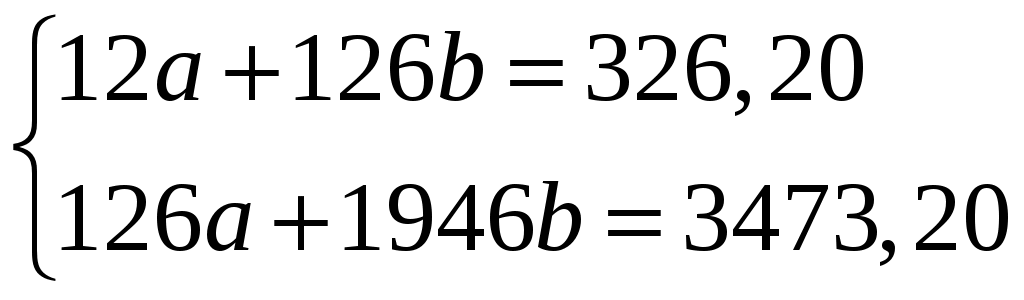
Решим систему уравнений по правилу Крамера:
Δ0 =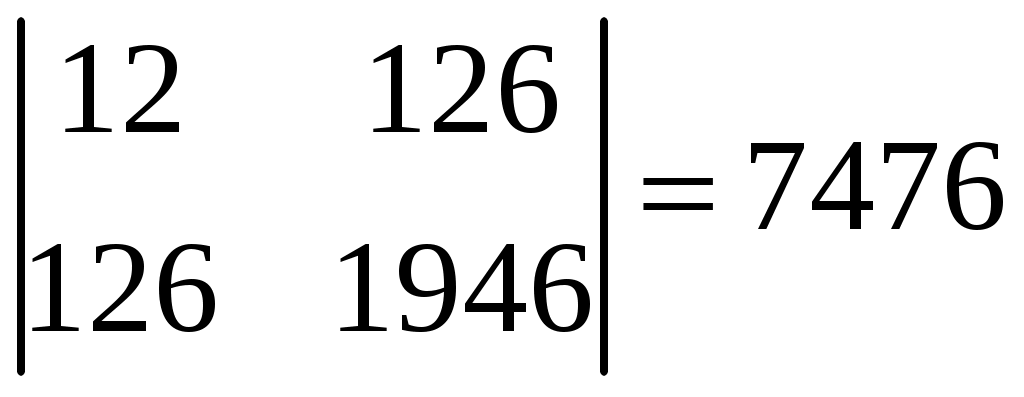
Δ1 =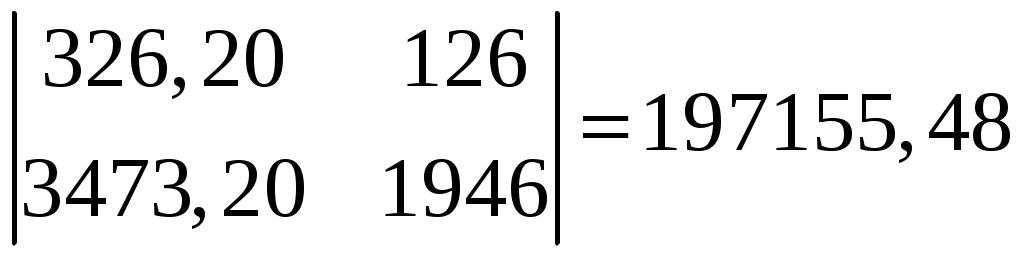
Δ2 =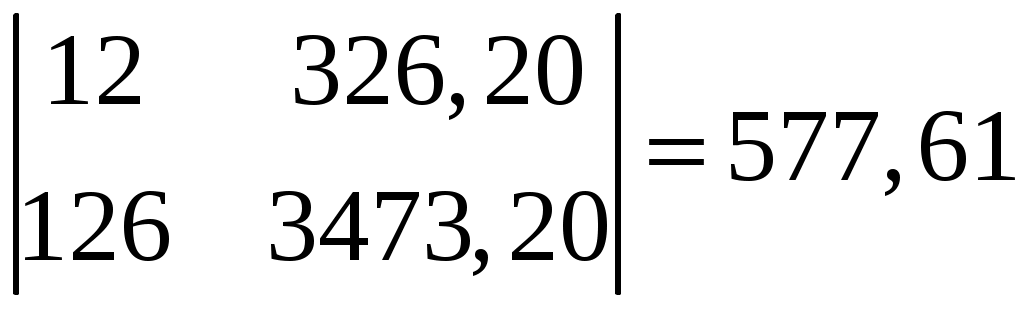
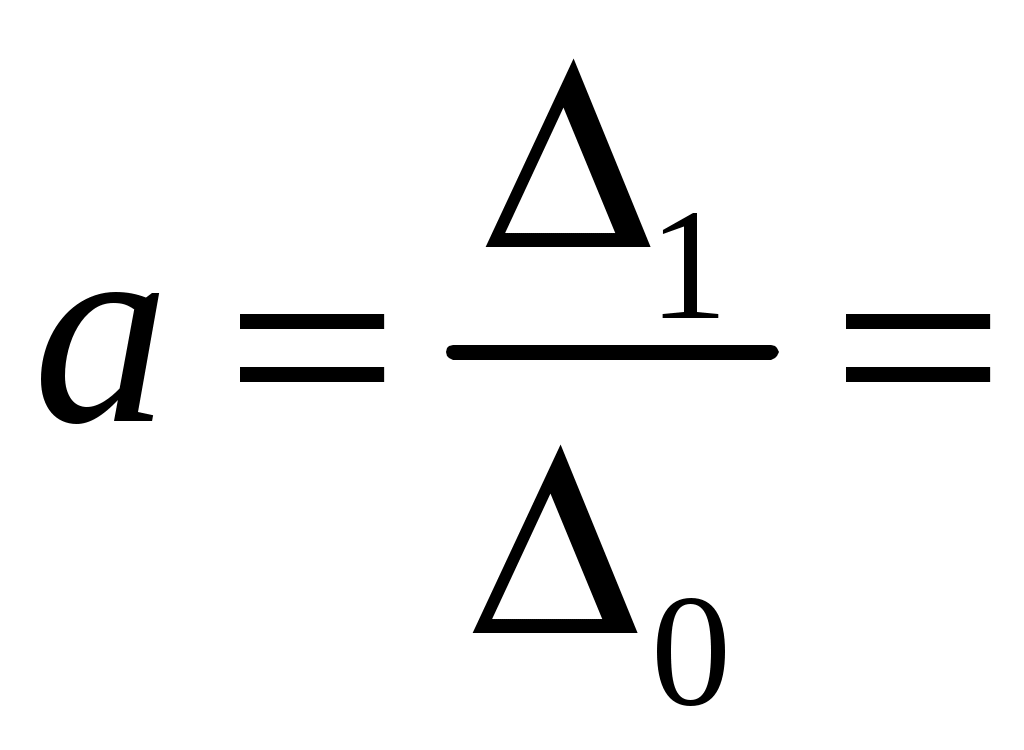
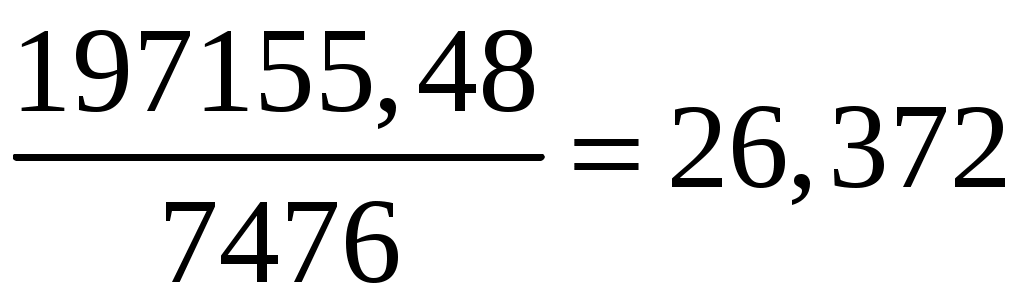 ,
,
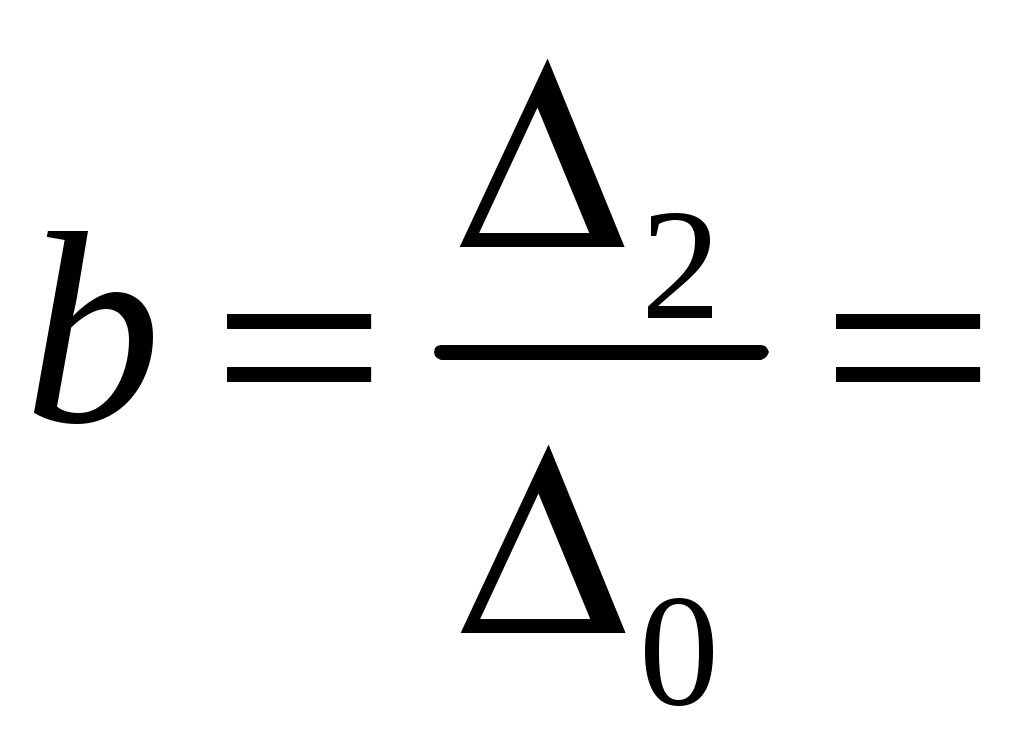
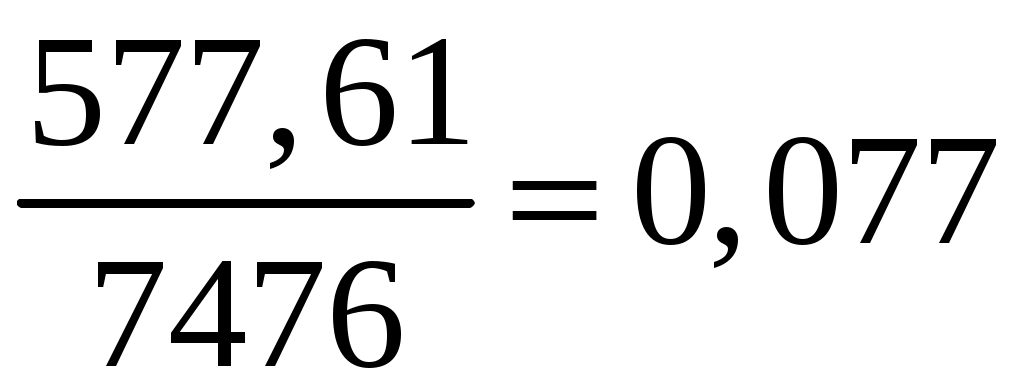 .
.
Результаты аналитического выравнивания следующие:
T = 26,372 + 0,077∙t.
Подставляя в это уравнение значения t = 1,...,266, найдем уровни T для каждого момента времени.
СПИСОК ЛИТЕРАТУРЫ
Для коэффициента b2 вероятность его не влияния на у равна 0,01 (1%), что меньше порогового значения в 5%, поэтому коэффициент b1 признается значимым и оставляется в модели.
Расчетные значения критерия Стьюдента следующие:;
Таким образом, признается статистическая значимость параметров
-
На основании полученных моделей рассчитать ожидаемое в среднем по предприятиям значение показателя эффективности деятельности при ожидаемых значениях факторов, приведенных в таблице исходных данных.
Прогнозное значение затрат на 1 руб. продукции
Прогнозное значение чистой прибыли:
Задача 3
Провести анализ динамики курса доллара в течение года (приложение) по своему варианту:
| Номер варианта | 2 |
| Год исследования | 2006 |
1. Провести выравнивание временного ряда методом скользящей средней.
2. Рассчитать сезонную компоненту S и устранить её из исходных членов ряда и получение выровненных данных.
Решение:
Исходные данные для анализа представлены в таблице:
| дата | t | yt | дата | t | yt | дата | t | yt |
| 30,12,2006 | 1 | 26,3311 | 01,09,2006 | 90 | 26,7295 | 04,05,2006 | 179 | 27,159 |
| 29,12,2006 | 2 | 26,3789 | 31,08,2006 | 91 | 26,7379 | 03,05,2006 | 180 | 27,2424 |
| 28,12,2006 | 3 | 26,3365 | 30,08,2006 | 92 | 26,7446 | 02,05,2006 | 181 | 27,2739 |
| 27,12,2006 | 4 | 26,36 | 29,08,2006 | 93 | 26,7672 | 29,04,2006 | 182 | 27,2739 |
| 26,12,2006 | 5 | 26,3528 | 28,08,2006 | 94 | 26,7998 | 28,04,2006 | 183 | 27,3621 |
| 25,12,2006 | 6 | 26,2941 | 26,08,2006 | 95 | 26,7998 | 27,04,2006 | 184 | 27,3921 |
| 23,12,2006 | 7 | 26,2941 | 25,08,2006 | 96 | 26,7863 | 26,04,2006 | 185 | 27,4244 |
| 22,12,2006 | 8 | 26,2928 | 24,08,2006 | 97 | 26,7614 | 25,04,2006 | 186 | 27,4331 |
| 21,12,2006 | 9 | 26,2759 | 23,08,2006 | 98 | 26,6964 | 22,04,2006 | 187 | 27,5198 |
| 20,12,2006 | 10 | 26,383 | 22,08,2006 | 99 | 26,705 | 21,04,2006 | 188 | 27,4666 |
| 19,12,2006 | 11 | 26,3884 | 19,08,2006 | 100 | 26,7364 | 20,04,2006 | 189 | 27,465 |
| 16,12,2006 | 12 | 26,3298 | 18,08,2006 | 101 | 26,7225 | 19,04,2006 | 190 | 27,5675 |
| 15,12,2006 | 13 | 26,2645 | 17,08,2006 | 102 | 26,7804 | 18,04,2006 | 191 | 27,6336 |
| 14,12,2006 | 14 | 26,2332 | 16,08,2006 | 103 | 26,8337 | 17,04,2006 | 192 | 27,7002 |
| 13,12,2006 | 15 | 26,2609 | 15,08,2006 | 104 | 26,8189 | 15,04,2006 | 193 | 27,7002 |
| 12,12,2006 | 16 | 26,2977 | 12,08,2006 | 105 | 26,793 | 14,04,2006 | 194 | 27,6985 |
| 09,12,2006 | 17 | 26,2356 | 11,08,2006 | 106 | 26,6738 | 13,04,2006 | 195 | 27,6625 |
| 08,12,2006 | 18 | 26,1917 | 10,08,2006 | 107 | 26,7391 | 12,04,2006 | 196 | 27,6797 |
| 07,12,2006 | 19 | 26,1883 | 09,08,2006 | 108 | 26,7348 | 11,04,2006 | 197 | 27,7085 |
| 06,12,2006 | 20 | 26,184 | 08,08,2006 | 109 | 26,6962 | 08,04,2006 | 198 | 27,6077 |
| 05,12,2006 | 21 | 26,2056 | 05,08,2006 | 110 | 26,771 | 07,04,2006 | 199 | 27,5332 |
| 02,12,2006 | 22 | 26,2465 | 04,08,2006 | 111 | 26,804 | 06,04,2006 | 200 | 27,5602 |
| 01,12,2006 | 23 | 26,3081 | 03,08,2006 | 112 | 26,7605 | 05,04,2006 | 201 | 27,6921 |
| 30,11,2006 | 24 | 26,3147 | 02,08,2006 | 113 | 26,8416 | 04,04,2006 | 202 | 27,7737 |
| 29,11,2006 | 25 | 26,3503 | 01,08,2006 | 114 | 26,8197 | 01,04,2006 | 203 | 27,6996 |
| 28,11,2006 | 26 | 26,3666 | 29,07,2006 | 115 | 26,8718 | 31,03,2006 | 204 | 27,7626 |
| 25,11,2006 | 27 | 26,5199 | 28,07,2006 | 116 | 26,8431 | 30,03,2006 | 205 | 27,8043 |
| 24,11,2006 | 28 | 26,556 | 27,07,2006 | 117 | 26,9878 | 29,03,2006 | 206 | 27,8019 |
| 23,11,2006 | 29 | 26,6122 | 26,07,2006 | 118 | 26,9073 | 28,03,2006 | 207 | 27,773 |
| 22,11,2006 | 30 | 26,6548 | 25,07,2006 | 119 | 26,9223 | 25,03,2006 | 208 | 27,847 |
| 21,11,2006 | 31 | 26,6402 | 22,07,2006 | 120 | 26,9122 | 24,03,2006 | 209 | 27,768 |
| 18,11,2006 | 32 | 26,6888 | 21,07,2006 | 121 | 26,9674 | 23,03,2006 | 210 | 27,7383 |
| 17,11,2006 | 33 | 26,6551 | 20,07,2006 | 122 | 27,0554 | 22,03,2006 | 211 | 27,7027 |
| 16,11,2006 | 34 | 26,6548 | 19,07,2006 | 123 | 27,0194 | 21,03,2006 | 212 | 27,6615 |
| 15,11,2006 | 35 | 26,6509 | 18,07,2006 | 124 | 26,9277 | 18,03,2006 | 213 | 27,7028 |
| 14,11,2006 | 36 | 26,6194 | 15,07,2006 | 125 | 26,9631 | 17,03,2006 | 214 | 27,8171 |
| 11,11,2006 | 37 | 26,6195 | 14,07,2006 | 126 | 26,9189 | 16,03,2006 | 215 | 27,8432 |
| 10,11,2006 | 38 | 26,6982 | 13,07,2006 | 127 | 26,867 | 15,03,2006 | 216 | 27,9929 |
| 09,11,2006 | 39 | 26,7044 | 12,07,2006 | 128 | 26,9125 | 14,03,2006 | 217 | 28,0079 |
| 08,11,2006 | 40 | 26,7218 | 11,07,2006 | 129 | 26,8558 | 11,03,2006 | 218 | 28,0203 |
| 07,11,2006 | 41 | 26,7007 | 08,07,2006 | 130 | 26,8781 | 10,03,2006 | 219 | 28 |
| 04,11,2006 | 42 | 26,7007 | 07,07,2006 | 131 | 26,9111 | 09,03,2006 | 220 | 27,9945 |
| 03,11,2006 | 43 | 26,7277 | 06,07,2006 | 132 | 26,8559 | 08,03,2006 | 221 | 27,9945 |
| 02,11,2006 | 44 | 26,7285 | 05,07,2006 | 133 | 26,8397 | 07,03,2006 | 222 | 27,881 |
| 01,11,2006 | 45 | 26,7811 | 04,07,2006 | 134 | 26,8735 | 04,03,2006 | 223 | 27,9305 |
| 31,10,2006 | 46 | 26,7477 | 03,07,2006 | 135 | 26,9423 | 03,03,2006 | 224 | 28,0279 |
| 28,10,2006 | 47 | 26,7884 | 01,07,2006 | 136 | 26,9423 | 02,03,2006 | 225 | 28,0245 |
| 27,10,2006 | 48 | 26,8305 | 30,06,2006 | 137 | 27,0789 | 01,03,2006 | 226 | 28,1211 |
| 26,10,2006 | 49 | 26,9025 | 29,06,2006 | 138 | 27,0611 | 28,02,2006 | 227 | 28,1223 |
| 25,10,2006 | 50 | 26,9307 | 28,06,2006 | 139 | 27,0334 | 27,02,2006 | 228 | 28,155 |
| 24,10,2006 | 51 | 26,8804 | 27,06,2006 | 140 | 27,1021 | 26,02,2006 | 229 | 28,1827 |
| 21,10,2006 | 52 | 26,851 | 24,06,2006 | 141 | 27,0491 | 25,02,2006 | 230 | 28,1827 |
| 20,10,2006 | 53 | 26,9351 | 23,06,2006 | 142 | 26,9738 | 23,02,2006 | 231 | 28,1827 |
| 19,10,2006 | 54 | 26,9288 | 22,06,2006 | 143 | 27,0163 | 22,02,2006 | 232 | 28,1908 |
| 18,10,2006 | 55 | 26,9445 | 21,06,2006 | 144 | 27,045 | 21,02,2006 | 233 | 28,1451 |
| 17,10,2006 | 56 | 26,969 | 20,06,2006 | 145 | 27,0379 | 20,02,2006 | 234 | 28,2182 |
| 14,10,2006 | 57 | 26,9314 | 17,06,2006 | 146 | 26,9869 | 18,02,2006 | 235 | 28,2182 |
| 13,10,2006 | 58 | 26,9508 | 16,06,2006 | 147 | 27,0369 | 17,02,2006 | 236 | 28,2225 |
| 12,10,2006 | 59 | 26,9537 | 15,06,2006 | 148 | 27,0895 | 16,02,2006 | 237 | 28,1994 |
| 11,10,2006 | 60 | 26,889 | 14,06,2006 | 149 | 27,0836 | 15,02,2006 | 238 | 28,1844 |
| 10,10,2006 | 61 | 26,8919 | 13,06,2006 | 150 | 27,0079 | 14,02,2006 | 239 | 28,2369 |
| 09,10,2006 | 62 | 26,8102 | 10,06,2006 | 151 | 27,0079 | 11,02,2006 | 240 | 28,2411 |
| 07,10,2006 | 63 | 26,8102 | 09,06,2006 | 152 | 26,8801 | 10,02,2006 | 241 | 28,2496 |
| 06,10,2006 | 64 | 26,7803 | 08,06,2006 | 153 | 26,8582 | 09,02,2006 | 242 | 28,2642 |
| 05,10,2006 | 65 | 26,7671 | 07,06,2006 | 154 | 26,7331 | 08,02,2006 | 243 | 28,2524 |
| 04,10,2006 | 66 | 26,7335 | 06,06,2006 | 155 | 26,7089 | 07,02,2006 | 244 | 28,2349 |
| 03,10,2006 | 67 | 26,7948 | 03,06,2006 | 156 | 26,8868 | 04,02,2006 | 245 | 28,1732 |
| 30,09,2006 | 68 | 26,7799 | 02,06,2006 | 157 | 27,0474 | 03,02,2006 | 246 | 28,1901 |
| 29,09,2006 | 69 | 26,7498 | 01,06,2006 | 158 | 26,9355 | 02,02,2006 | 247 | 28,1042 |
| 28,09,2006 | 70 | 26,7944 | 31,05,2006 | 159 | 26,984 | 01,02,2006 | 248 | 28,1305 |
| 27,09,2006 | 71 | 26,7263 | 30,05,2006 | 160 | 27,0652 | 31,01,2006 | 249 | 28,1207 |
| 26,09,2006 | 72 | 26,6665 | 29,05,2006 | 161 | 27,0349 | 28,01,2006 | 250 | 28,024 |
| 23,09,2006 | 73 | 26,6712 | 27,05,2006 | 162 | 27,0349 | 27,01,2006 | 251 | 27,9698 |
| 22,09,2006 | 74 | 26,7674 | 26,05,2006 | 163 | 27,0381 | 26,01,2006 | 252 | 27,9805 |
| 21,09,2006 | 75 | 26,7974 | 25,05,2006 | 164 | 27,0168 | 25,01,2006 | 253 | 27,9898 |
| 20,09,2006 | 76 | 26,7715 | 24,05,2006 | 165 | 26,9876 | 24,01,2006 | 254 | 28,0512 |
| 19,09,2006 | 77 | 26,8048 | 23,05,2006 | 166 | 27,0965 | 21,01,2006 | 255 | 28,2909 |
| 16,09,2006 | 78 | 26,7667 | 20,05,2006 | 167 | 26,9987 | 20,01,2006 | 256 | 28,2863 |
| 15,09,2006 | 79 | 26,8015 | 19,05,2006 | 168 | 27,0663 | 19,01,2006 | 257 | 28,3023 |
| 14,09,2006 | 80 | 26,798 | 18,05,2006 | 169 | 26,9569 | 18,01,2006 | 258 | 28,2697 |
| 13,09,2006 | 81 | 26,7764 | 17,05,2006 | 170 | 27,0209 | 17,01,2006 | 259 | 28,3007 |
| 12,09,2006 | 82 | 26,7965 | 16,05,2006 | 171 | 26,9187 | 16,01,2006 | 260 | 28,474 |
| 09,09,2006 | 83 | 26,7625 | 13,05,2006 | 172 | 26,9431 | 14,01,2006 | 261 | 28,474 |
| 08,09,2006 | 84 | 26,6708 | 12,05,2006 | 173 | 27,0755 | 13,01,2006 | 262 | 28,3966 |
| 07,09,2006 | 85 | 26,6714 | 11,05,2006 | 174 | 27,0359 | 12,01,2006 | 263 | 28,4834 |
| 06,09,2006 | 86 | 26,6406 | 10,05,2006 | 175 | 27,0801 | 11,01,2006 | 264 | 28,4821 |
| 05,09,2006 | 87 | 26,7222 | 07,05,2006 | 176 | 27,0801 | 10,01,2006 | 265 | 28,7825 |
| 04,09,2006 | 88 | 26,7542 | 06,05,2006 | 177 | 27,1258 | 07,01,2006 | 266 | 28,7825 |
| 02,09,2006 | 89 | 26,7542 | 05,05,2006 | 178 | 27,2085 | | | |
Исходная динамика курса доллара представлена на рис. 1.

рис. 1
Укрупним интервал, рассчитав среднемесячный курс валюты
| t | yt |
| 1 | 26,28841 |
| 2 | 26,6212 |
| 3 | 26,86461 |
| 4 | 26,74668 |
| 5 | 26,7635 |
| 6 | 26,91703 |
| 7 | 26,98456 |
| 8 | 27,06277 |
| 9 | 27,57065 |
| 10 | 27,87902 |
| 11 | 28,1946 |
| 12 | 28,30339 |
1. Проведем выравнивание временного ряда методом скользящей средней:
Найдем скользящие средние. Полученные таким образом выровненные значения уже не содержат сезонной компоненты.
Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.
| | t | yt | Скользящая средняя | Центрированная скользящая средняя | Оценка сезонной компоненты |
| | 1 | 26,28841 | | | |
| | 2 | 26,6212 | 26,630225 | | |
| | 3 | 26,86461 | 26,7489975 | 26,68961125 | 0,17499875 |
| | 4 | 26,74668 | 26,822955 | 26,78597625 | -0,03929625 |
| | 5 | 26,7635 | 26,8529425 | 26,83794875 | -0,07444875 |
| | 6 | 26,91703 | 26,931965 | 26,89245375 | 0,02457625 |
| | 7 | 26,98456 | 27,1337525 | 27,03285875 | -0,04829875 |
| | 8 | 27,06277 | 27,37425 | 27,25400125 | -0,19123125 |
| | 9 | 27,57065 | 27,67676 | 27,525505 | 0,045145 |
| | 10 | 27,87902 | 27,986915 | 27,8318375 | 0,0471825 |
| | 11 | 28,1946 | | | |
| | 12 | 28,30339 | | | |
2. Рассчитать сезонную компоненту S и устранить её из исходных членов ряда и получение выровненных данных.
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Эти оценки используются для расчета сезонной компоненты S. Для этого найдем средние за каждый период оценки сезонной компоненты Sj. Сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
| Показатели | 1 | 2 | 3 | 4 |
| 1 | | | 0,1750 | -0,0393 |
| 2 | -0,0744 | 0,0246 | -0,0483 | -0,1912 |
| 3 | 0,0451 | 0,0472 | | |
| Всего за период | -0,0293 | 0,0718 | 0,1267 | -0,2305 |
| Средняя оценка сезонной компоненты | -0,0147 | 0,0359 | 0,0633 | -0,1153 |
| Скорректированная сезонная компонента, Si | -0,0070 | 0,0436 | 0,0710 | -0,1076 |
Рассчитываем скорректированные значения сезонной компоненты Si и заносим полученные данные в таблицу. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины T + E = Y - S. Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Определим компоненту T данной модели. Для этого проведем аналитическое выравнивание ряда (T + E) с помощью линейного тренда.
Для определения параметров уравнения
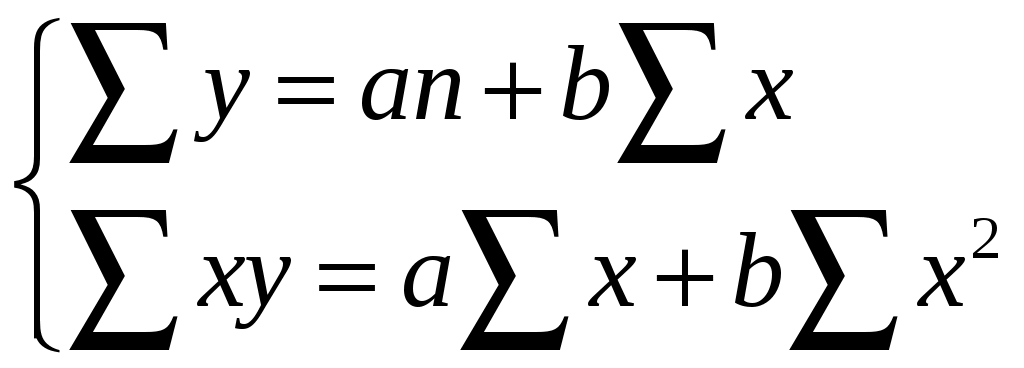
Подставим полученные данные в систему уравнений:
Решим систему уравнений по правилу Крамера:
Δ0 =
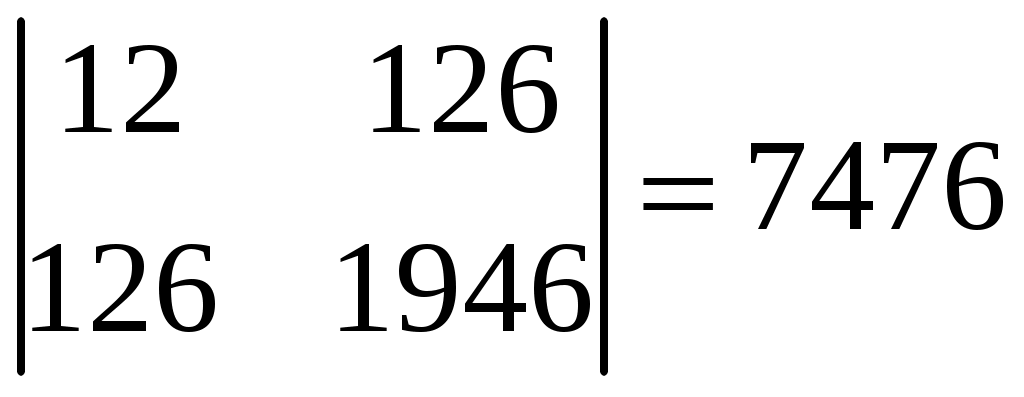
Δ1 =
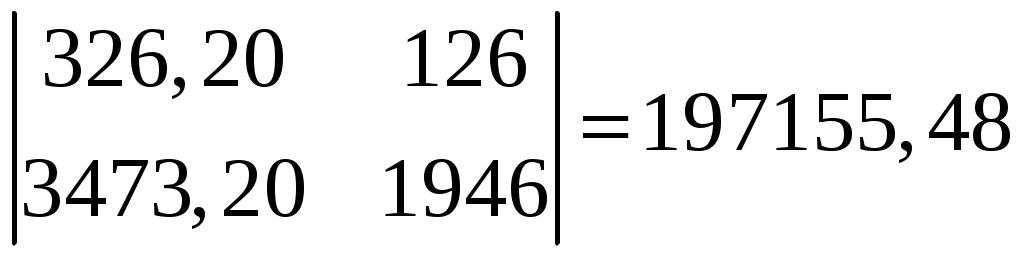
Δ2 =
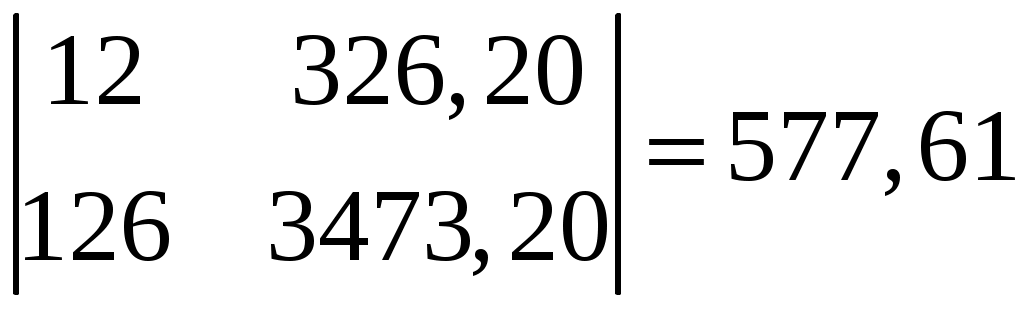
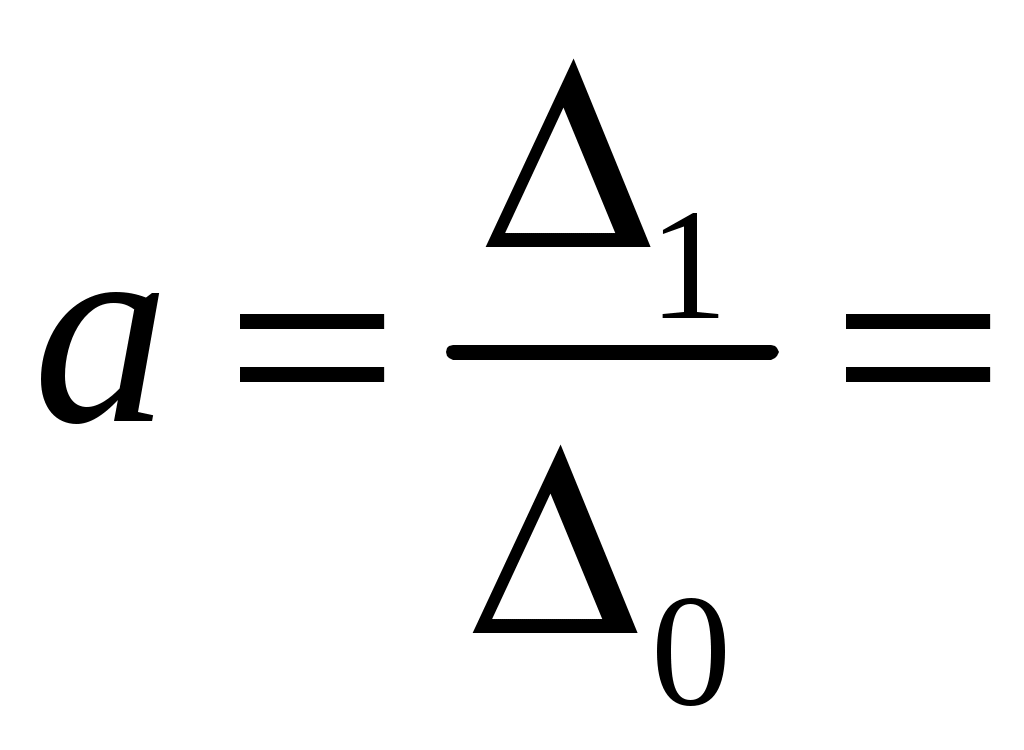
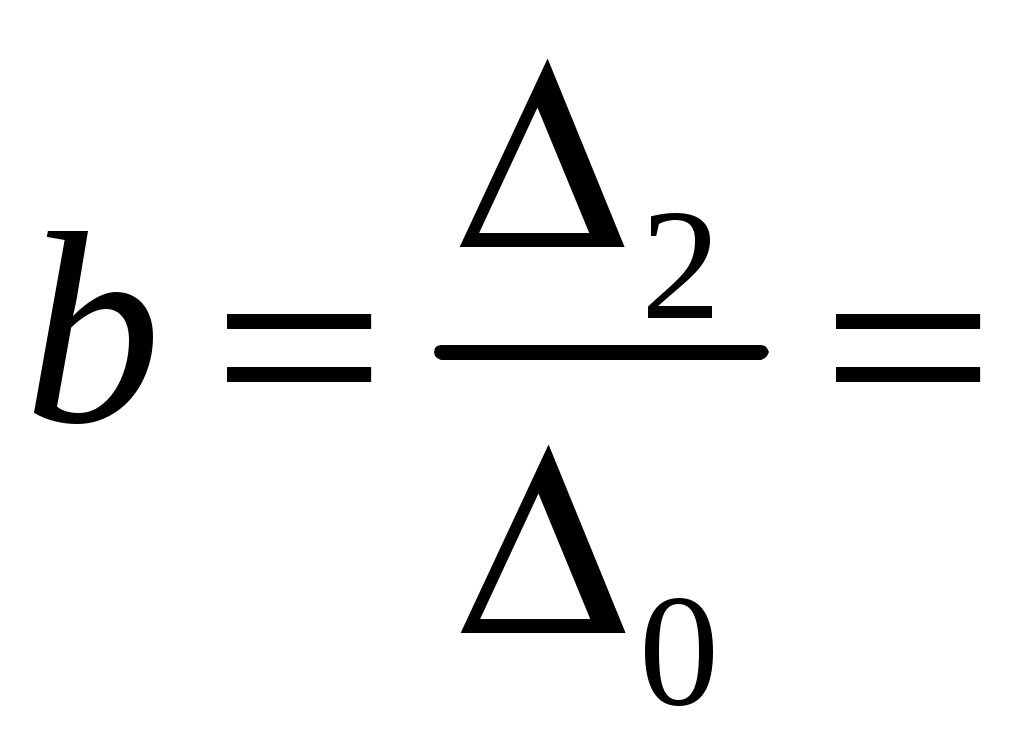
Результаты аналитического выравнивания следующие:
T = 26,372 + 0,077∙t.
Подставляя в это уравнение значения t = 1,...,266, найдем уровни T для каждого момента времени.
| | t | yt | Si | yt - Si | T | T + Si | E = yt - (T + Si) | E2 |
| | 1 | 26,28841 | -0,01 | 26,30 | 26,45 | 26,44 | -0,15 | 0,02 |
| | 4 | 26,6212 | 0,04 | 26,58 | 26,53 | 26,57 | 0,05 | 0,00 |
| | 9 | 26,86461 | 0,07 | 26,79 | 26,60 | 26,67 | 0,19 | 0,04 |
| | 16 | 26,74668 | -0,11 | 26,85 | 26,68 | 26,57 | 0,17 | 0,03 |
| | 25 | 26,7635 | -0,01 | 26,77 | 26,76 | 26,75 | 0,01 | 0,00 |
| | 36 | 26,91703 | 0,04 | 26,87 | 26,84 | 26,88 | 0,04 | 0,00 |
| | 225 | 26,98456 | 0,07 | 26,91 | 27,53 | 27,60 | -0,62 | 0,38 |
| | 256 | 27,06277 | -0,11 | 27,17 | 27,61 | 27,50 | -0,44 | 0,19 |
| | 289 | 27,57065 | -0,01 | 27,58 | 27,69 | 27,68 | -0,11 | 0,01 |
| | 324 | 27,87902 | 0,04 | 27,84 | 27,76 | 27,81 | 0,07 | 0,01 |
| | 361 | 28,1946 | 0,07 | 28,12 | 27,84 | 27,91 | 0,28 | 0,08 |
| | 400 | 28,30339 | -0,11 | 28,41 | 27,92 | 27,81 | 0,49 | 0,24 |
| сумма | 1946 | 326,19642 | | 326,20 | | | 0,00 | 1,01 |

СПИСОК ЛИТЕРАТУРЫ
-
Бородич С.А. Эконометрика. – Мн.: Новое знание, 2004. -
Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 1999. -
Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ, 2002. -
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. – М.: Дело, 2004. -
Орлов А.И. Эконометрика. – М.: Экзамен, 2002. -
Суслов В.И., Ибрагимов Н.М., Талышева Л.П. Эконометрия. – Новосибирск.: СО РАН, 2005. -
Харин Ю.С., Малюгин В.И., Харин А.Ю. Эконометрическое моделирование. – Мн.: БГУ, 2003.