Добавлен: 10.11.2023
Просмотров: 72
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Таблица 3.1 –Параметры материала сердцевины волокна.
| Длина волны, мкм Параметры | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1.8 |
| n | 1.467 | 1.465 | 1.462 | 1.46 | 1.458 | 1.455 |
| NГР | 1.481 | 1.478 | 1.476 | 1.476 | 1.478 | 1.479 |
| DМ, пс/ (нм ·км) | -109.96 | -40.91 | -7.41 | 12.43 | 27.57 | 40.24 |
| DВ, пс/ (нм ·км) | -6.91 | -8.64 | -10.37 | -12.1 | -13.83 | -15.56 |
| DХР, пс/ (нм ·км) | -116.87 | -49.55 | -17.78 | 0.33 | 13.74 | 24.68 |
Таблица 3.2 – Значения показателей преломления и дисперсий.
-
Рассчитаем показатель преломления для следующих длин волн: 0,8; 1,0; 1,2; 1,4; 1,6; 1,8 мкм.
По формуле Селмайера:
=
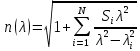
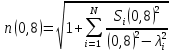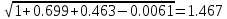
n (1,0) =
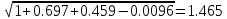
n (1,2) =
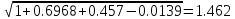
n (1,4) =
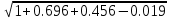= 1.46n (1,6) =
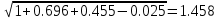
n (1,8) =
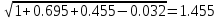
| Длина волны, мкм | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1.8 |
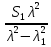 | 0.699 | 0.697 | 0.6968 | 0.696 | 0.696 | 0.695 |
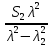 | 0.463 | 0.459 | 0.457 | 0.456 | 0.455 | 0.455 |
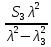 | -0.0061 | -0.0096 | -0.0139 | -0.019 | -0.025 | -0.032 |
| n ( 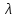 ) | 1.467 | 1.465 | 1.462 | 1.46 | 1.458 | 1.455 |
Таблица 3.3 – Промежуточные расчёты.
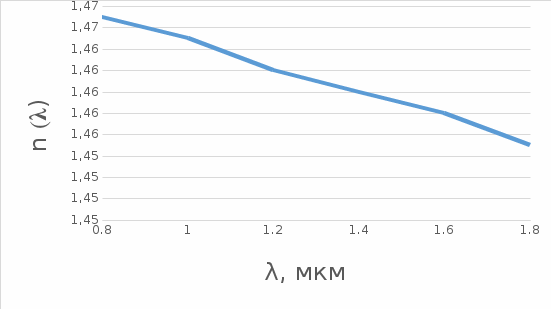
Рисунок 3.1 График зависимости рассчитанного показателя преломления n от длины волны на интервале от 0,8 до
1,8 мкм| Длина волны, мкм | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 |
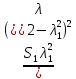 | 0.00638 | 0.0026 | 0.00125 | 0.00067 | 0.00039 | 0.00024 |
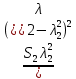 | 0.0166 | 0.00671 | 0.0032 | 0.00172 | 0.001 | 0.00062 |
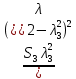 | 0.00966 | 0.00975 | 0.00987 | 0.01 | 0.0101 | 0.0103 |
| Nгр | 1.481 | 1.478 | 1.476 | 1.476 | 1.478 | 1.479 |
Таблица 3.4 – Промежуточные расчеты.
-
Нахождение группового показателя преломления для сердцевины волокна.
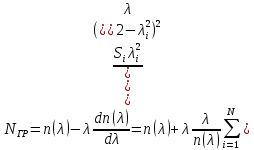
где
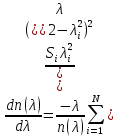
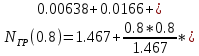0.00966)=1.481
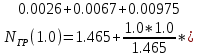)=1.478
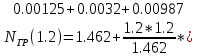)=1.476
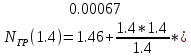+0.00172)+0.01=1.476
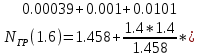)=1.478
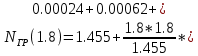0.0103)=1.479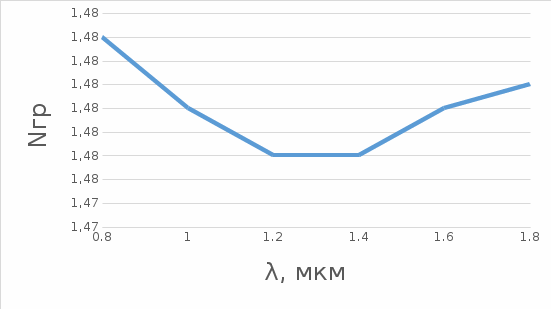
Рисунок 3.2 - График зависимости группового показателя преломления от длины волны на интервале от 0,8 до 1,8 мкм.
-
Нахождение коэффициента удельной материальной дисперсии волокна.
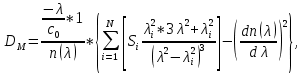
c0 – скорость света в свободном пространстве.
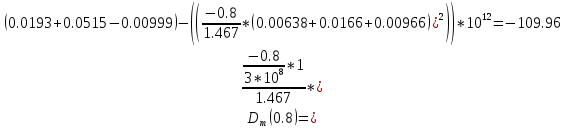
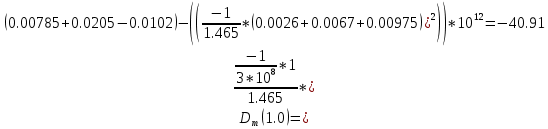
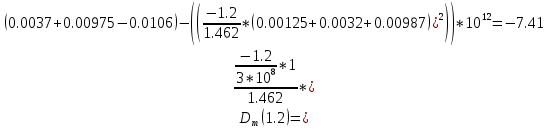
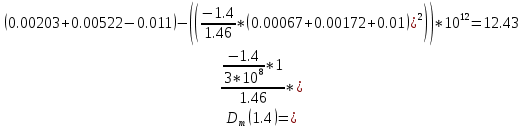
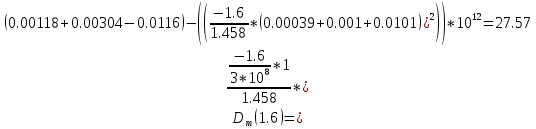
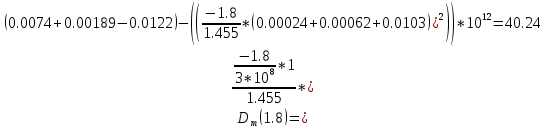
| Длина волны, мкм | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1.8 |
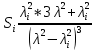 | 0.0193 | 0.00785 | 0.0037 | 0.00203 | 0.00118 | 0.00074 |
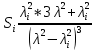| | 0.0515 | 0.0205 | 0.00975 | 0.00522 | 0.00304 | 0.00189 |
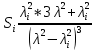| | -0.00999 | -0.0102 | -0.0106 | -0.0110 | -0.0116 | -0.0122 |
| DM пс/(нм*км) | -109.96 | -40.91 | -7.41 | 12.43 | 27.57 | 40.24 |
Таблица 3.5 – Промежуточные расчеты.
-
Нахождение коэффициента удельной волноводной дисперсии волокна в предположении, что волокно работает в одномодовом режиме.
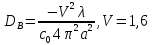
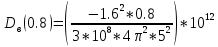=-6.91
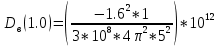=-8.64
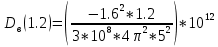=-10.37
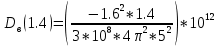=-12.1
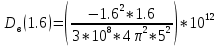=-13.83
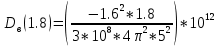=-15.56-
Нахождение коэффициента удельной хроматической дисперсии волокна.
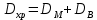
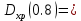-109.96-6.91=-116.87
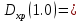-40.91-8.64=-49.55
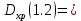-7.41-10.37=-17.78
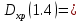12.43-12.1=0.33
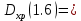27.57-13.83=13.74
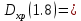40.24-15.56=24.68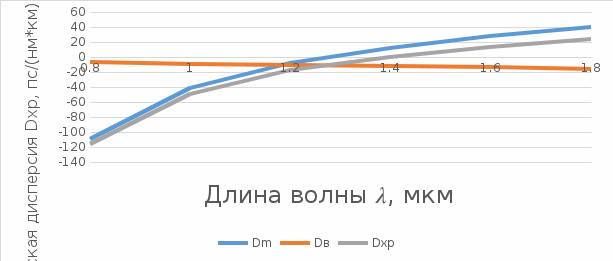
Рисунок 3.3 – график зависимости удельных дисперсий от длины волны для типичного одноходового волокна
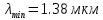
IV часть. Оценка искажения импульсов при распространении по оптическим волокнам.
Изучите конспект лекций, учебную литературу и c помощью методических указаний IV части выполните следующие пункты согласно вашему варианту задания. Все необходимые числовые значения параметров для расчёта приведены в тaбл.4.1, тa6л.4.2 и в Приложениях 1–5:
-
По заданным значениям гауссовского оптического импульса (тaбл.4.1) рассчитать зависимость нормированных значений огибающей напряжённости электрического поля импульса от времени на входе оптического волокна E (0, t). Заполнить тa6л.4.3. Нарисовать зависимость E (0, t). -
По заданному типу оптического волокна (тa6л.4.2 и Приложения 1–5) найти дисперсионные параметры, затухание и рассчитать зависимость нормированных значений огибающей напряжённости электрического поля импульса от времени после распространения на расстояние L1 и L2. Заполнить тaбл.4.3. Нарисовать зависимости E (L1, t) и E(L2, t) на одном рисунке. -
Рассчитать зависимость значения девиации частоты (в ГГц), несущей оптического импульса от времени на расстоянии L2. Заполнить тa6л.4.3. Нарисовать зависимость ????ƒ(????). Схематически oтo6pasить оптический импульс c девиацией частоты без сохранения мacштa6a. -
Предположив, что по оптическому волокну передастся кодовая последовательность «101» в виде оптических импульсов гауссовой формы, прочем «1» соответствует гауссовом импульсу, a «0» - отсутствию излучения, нeo6xoдимo нарисовать на одном рисунке временную зависимость oги6aющиx электрического поля этих импульсов после распространения на расстояние L2. Китовый интервал последовательности импульсов принять равным 2T0. Сделать вывод o возможности достоверного прима этой последовательности на расстоянии L2.
| T0, пс | λ, мкм | Тип ОВ рек. ITU-T | L1 км | L2 км |
| 10 | 1,465 | G.656 | 30 | 60 |
Таблица 4.1 – Исходные данные.
| t | -4T0 | -7T0/2 | -3T0 | -5T0/2 | -2T0 | -3T0/2 | -T0 | -T0/2 |
| E (0, t) | 0,00033 | 0,0021 | 0,011 | 0,043 | 0,13 | 0,32 | 0,6 | 0,88 |
| E (L1, t) | 0.042 | 0.084 | 0,14 | 0,24 | 0,37 | 0,51 | 0,64 | 0,74 |
| E (L2, t) | 0,037 | 0,074 | 0,13 | 0,22 | 0,33 | 0,45 | 0,57 | 0,65 |
| df, ГГц | -97,2 | -85 | -72,9 | -60,7 | -48,6 | -36,4 | -24,3 | -12,1 |
| t | 0 | T0/2 | T0 | 3T0/2 | 2T0 | 5T0/2 | 3T0 | 7T0/2 | 4T0 |
| E (0, t) | 1 | 0,88 | 0,6 | 0,32 | 0,13 | 0,043 | 0,011 | 0,0021 | 0,00033 |
| E (L1, t) | 0,78 | 0,74 | 0,64 | 0,51 | 0,37 | 0,24 | 0,14 | 0,084 | 0,042 |
| E (L2, t) | 0,69 | 0,65 | 0,57 | 0,45 | 0,33 | 0,22 | 0,13 | 0,074 | 0,037 |
| df, ГГц | 0 | 12,1 | 24,3 | 36,4 | 48,6 | 60,7 | 72,9 | 85 | 97,2 |