Файл: Решение задачи Для этого построим координатную плоскость. На плоскости строим границу области допустимых планов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Постановка задачи
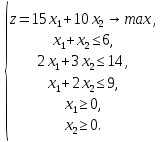
Графическое решение задачи
Для этого построим координатную плоскость.
1. На плоскости строим границу области допустимых планов.
Первая прямая
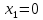 – вертикальная ось.
– вертикальная ось. Вторая прямая
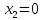 – горизонтальная ось.
– горизонтальная ось.Третья прямая
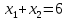 . Для построения находим точки пересечения с осями. Вертикальная ось:
. Для построения находим точки пересечения с осями. Вертикальная ось: 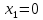 ,
, 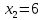 . Горизонтальная ось:
. Горизонтальная ось: 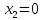 ,
, 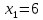 .
.Четвертая прямая
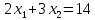 . Точки пересечения с осями. Вертикальная ось:
. Точки пересечения с осями. Вертикальная ось: 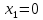 ,
, 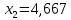 . Горизонтальная ось:
. Горизонтальная ось: 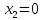 ,
, 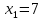 .
.Пятая прямая
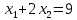 . Точки пересечения с осями. Вертикальная ось:
. Точки пересечения с осями. Вертикальная ось: 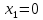 ,
, 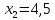 . Горизонтальная ось:
. Горизонтальная ось: 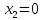 ,
, 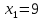 .
.Выбираем полуплоскости, соответствующие неравенствам.
Первая прямая:
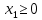 – правая полуплоскость.
– правая полуплоскость. Вторая прямая:
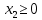 – верхняя полуплоскость.
– верхняя полуплоскость.Третья прямая:
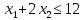 – нижняя полуплоскость.
– нижняя полуплоскость.Четвертая прямая:
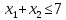 – нижняя полуплоскость.
– нижняя полуплоскость.
Пятая прямая:
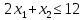 – нижняя полуплоскость.
– нижняя полуплоскость.В пересечении – пятиугольник на рисунке 1. Таким образом, область допустимых планов – пятиугольник.
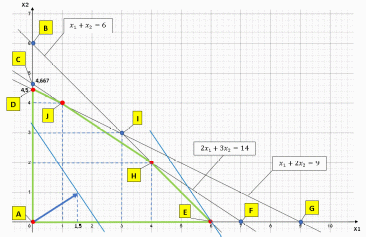
Рис. 1 – Графическое решение задачи
2. Для нахождения оптимального решения задачи на плоскости производим следующие построения.
Вектор направления целевой функции (2,3), координаты которого пропорциональны коэффициентам целевой функции
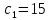 ,
, 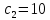 . На рисунке 1 синий вектор.
. На рисунке 1 синий вектор.Прямая линия постоянного уровня целевой функции, перпендикулярная построенному вектору. На рисунке 1 нижняя синяя пунктирная линия.
Передвигаем линию в направлении построенного вектора до крайней вершины построенного пятиугольника. На рисунке 1 верхняя синяя пунктирная линия.
Крайняя вершина – точка H пересечения третьей и четвертой прямых определяет оптимальное решение задачи.
3. Находим координаты крайней вершины.
Решаем систему уравнений
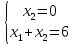
Подставляя
 получаем
получаем  . Таким образом, оптимальный план равен
. Таким образом, оптимальный план равен 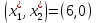 . Подставляя в целевую функцию, находим
. Подставляя в целевую функцию, находим 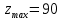 .
.Каноническая форма задачи
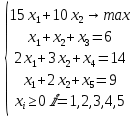
Решение задачи методом полного перебора
Построение опорных планов. Рассматривается система уравнений
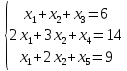
Из набора
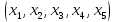 выбираются две переменные (небазисные), равные нулю. Подставляя эти значения в заданную систему уравнений и решая ее, находятся значения остальных переменных (базисных). В случае, если одно из значений переменных опорного плана отрицательно, такой план является недопустимым. Для допустимых планов подсчитаны значения целевой функции. Полученные значения представлены в таблице 1.
выбираются две переменные (небазисные), равные нулю. Подставляя эти значения в заданную систему уравнений и решая ее, находятся значения остальных переменных (базисных). В случае, если одно из значений переменных опорного плана отрицательно, такой план является недопустимым. Для допустимых планов подсчитаны значения целевой функции. Полученные значения представлены в таблице 1.
Таблица 1 – Решение задачи методом перебора
| План | 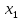 | 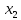 | 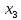 | 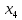 | 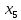 | 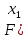 , , 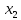 ) ) |
| A | 0 | 0 | 6 | 14 | 9 | 0 |
| B | 0 | 6 | 0 | -4 | -3 | н/д |
| C | 0 | 4,667 | 1,333 | 0 | -0,334 | н/д |
| D | 0 | 4,5 | 1,5 | 0,5 | 0 | 45 |
| E | 6 | 0 | 0 | 2 | 3 | 90 |
| F | 7 | 0 | -1 | 0 | 2 | н/д |
| G | 9 | 0 | -3 | -4 | 0 | н/д |
| H | 4 | 2 | 0 | 0 | 1 | 80 |
| I | 3 | 3 | 0 | -1 | 0 | н/д |
| J | 1 | 4 | 1 | 0 | 0 | 55 |
Оптимальным является опорный план Е, что подтверждает правильность решения задачи графическим способом.