ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 92
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Квантовая оптика
Тепловое излучение
6.230 [5.263]
Имеется два абсолютно черных источника теплового излучения. Температура одного из них Т1=2500 К Найти температуру другого источника, если длина волны, отвечающая максимуму его испускательной способности, на
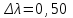 мкм больше длины волны, соответствующей максимуму испускательной способности первого источника (постоянная Вина –
мкм больше длины волны, соответствующей максимуму испускательной способности первого источника (постоянная Вина – 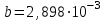 м·К).
м·К). 6.231 [5.264]
Энергетическая светимость абсолютно черного тела Мэ=3,0 Вт/см2. Определить длину волны, отвечающую максимуму испускательной способности этого тела ( постоянная Вина –
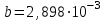 м·К, постоянная Стефана-Больцмана –
м·К, постоянная Стефана-Больцмана – 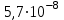 Вт·м-2·К-4 ).
Вт·м-2·К-4 ). 6.232 [5.265]
Излучение Солнца по своему спектральному составу близко к излучению абсолютно черного тела, для которого максимум испускательной способности приходится на длину волны 0,48 мкм. Найти массу, теряемую Солнцем ежесекундно за счет этого излучения. Оцените время, за которое масса Солнца уменьшится на 1 %.
6.234 [5.267]
Медный шарик диаметра
6.235 [5.268]
Температура поверхности Солнца
. Расстояние от Солнца до Земли
Квантовые свойства света
5.6 [5.280]
Лазер излучил в импульсе длительностью
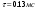 пучок света с энергией
пучок света с энергией 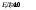 . Найти среднее давление такого светового импульса, если его сфокусировать в пятнышко диаметром
. Найти среднее давление такого светового импульса, если его сфокусировать в пятнышко диаметром 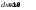 на поверхность, перпендикулярную к пучку, с коэффициентом отражения
на поверхность, перпендикулярную к пучку, с коэффициентом отражения 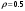 .
.5.14 [5.288]
При увеличении напряжения на рентгеновской трубке в =1,5 раза длина волны коротковолновой границы сплошного рентгеновского спектра изменилась на =26 пм. Найти первоначальное напряжение на трубке.
(
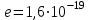 Кл,
Кл, 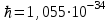 Дж·с,
Дж·с, 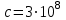 м·с)
м·с)5.18 [5.292]
Определите красную границу фотоэффекта для цинка и максимальную скорость фотоэлектронов, вырываемых с его поверхности электромагнитным излучением с длиной волны 250 нм.
5.19 [5.293]
При поочередном освещении поверхности некоторого металла светом с 1=0,35 мкм и 2=0,54 мкм обнаружили, что соответствующие максимальные скорости фотоэлектронов отличаются друг от друга в =2 раза. Найти работу выхода с поверхности этого металла.
(
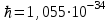 Дж·с,
Дж·с, 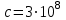 м·с)
м·с)5.28 [5.302]
Узкий пучок монохроматического рентгеновского излучения падает на рассеивающее вещество. При этом длины волн смещенных составляющих излучения, рассеянного под углами
5.30 [5.304]
Фотон с длиной волны =6,0 пм рассеялся под прямым углом на покоившемся свободном электроне. Найти:
а) частоту рассеянного фотона;
б) кинетическую энергию электрона отдачи.
Корпускулярно-волновой дуализм
Волны де Бройля.
5.87 [6.50]
Ч
 астица движется слева направо в одномерном потенциальном поле, см. рис. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы T = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер?
астица движется слева направо в одномерном потенциальном поле, см. рис. Левее барьера, высота которого U = 15 эВ, кинетическая энергия частицы T = 20 эВ. Во сколько раз и как изменится дебройлевская длина волны частицы при переходе через барьер?5.96 [6.59]
Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины b = 1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстоянии l = 50 см, ширина центрального дифракционного максимума
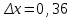 мм.
мм.5.97 [6.60]
Параллельный поток электронов, ускоренных разностью потенциалов U = 25 B, падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 50 мкм. Определить расстояние между двумя соседними максимумами дифракционной картины на экране, расположенном на расстоянии l = 100 см от щелей.
Соотношения (принцип) неопределённостей Гейзенберга
[6.72]
Электрон с кинетической энергией
5.112 [6.75]
Частица массы m движется в одномерном потенциальном поле U = kx2/2 (гармонический осциллятор). Оценить с помощью соотношения неопределённостей минимально возможную энергию частицы в таком поле.
Боровская модель атома водорода
5.58 [6.23]
Найти для водородоподобного иона радиус n-й боровской орбиты и скорость электрона на ней. Вычислить эти величины для первой боровской орбиты атома водорода и иона Не
+.
(
 Кл,
Кл,  Дж·с,
Дж·с, 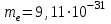 кг,
кг,  м·с,
м·с, 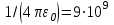 м/Ф,
м/Ф, 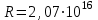 с-1 – постоянная Ридберга)
с-1 – постоянная Ридберга)5.59 [6.24]
Определить
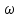 — круговую частоту обращения электрона на n-й круговой боровской орбите водородоподобного иона. Вычислить эту величину для иона Не+ при n=2.
— круговую частоту обращения электрона на n-й круговой боровской орбите водородоподобного иона. Вычислить эту величину для иона Не+ при n=2.(
 Кл,
Кл,  Дж·с,
Дж·с, 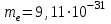 кг,
кг,  м·с,
м·с, 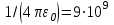 м/Ф,
м/Ф, 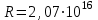 с-1 – постоянная Ридберга)
с-1 – постоянная Ридберга)5.60 [6.25]
Определить для атома водорода и иона Не+: энергию связи электрона в основном состоянии, потенциал ионизации, первый потенциал возбуждения и длину волны головной линии серии Лаймана.
(
 Кл,
Кл,  Дж·с,
Дж·с, 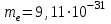 кг,
кг,  м·с,
м·с, 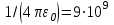 м/Ф,
м/Ф, 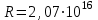 с-1 – постоянная Ридберга)
с-1 – постоянная Ридберга)5.62 [6.26]
Какую наименьшую энергию надо сообщить иону He+, находящемуся в основном состоянии, чтобы он смог испустить фотон, соответствующий головной линии серии Бальмера ?
(
 Кл,
Кл,  Дж·с,
Дж·с, 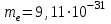 кг,
кг,  м·с,
м·с, 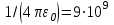 м/Ф,
м/Ф, 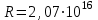
с-1 – постоянная Ридберга)
5.74 [6.38]
Энергия связи электрона в основном состоянии атома He равна Е0=24.6 эВ. Найти энергию, необходимую для удаления обоих электронов из этого атома.
Уравнение Шрёдингера.
5.124 [6.80]
Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергии между уровнями с n1 = 2 и n2 = 3 составляет Е = 0,30 эВ.
5.125 [6.81]
Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины l c абсолютно непроницаемыми стенками (0<x<l). Найти вероятность пребывания частицы в области l/3<x<2l/3.
Многоэлектронные атомы
5.165 [6.112]
Сколько и какие значения квантового числа
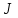 может иметь атом в состоянии с квантовыми числами
может иметь атом в состоянии с квантовыми числами 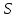 и
и 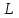 , равными соотоветственно:
, равными соотоветственно:а) 2 и 3; б) 3 и 3; в)
 и 2?
и 2?5.166 [6.113]
Найти возможные значения полных механических моментов атомов, находящихся в состояниях 4P и 5D?
5.169 [6.116]
Атом находится в состоянии, мультиплетность которого равна трем, а полный механический момент
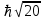 Каким может быть соответствующее квантовое число L?
Каким может быть соответствующее квантовое число L?5.170 [6.117]
Определить максимально возможный механический момент атома в состоянии, мультиплетность которого равна пяти и кратность вырождения по J – семи. Написать спектральное обозначение соответствующего терма.
5.175 [6.122]
Установить, какие из нижеперечисленных переходов запрещены правилами отбора: