Файл: Дискретные элементы и дискретные устройства понятия, свойства, класся Элемент.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 53
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Дискретные элементы и дискретные устройства: понятия, свойства, класс-я
Элемент – некот совокупность элементов, кот. выполняющие одну функцию или операции.
Дискретные элемент – совокупность деталей объеден в общую схему для выполнения зад функции и меняющих свое вых значение скочкообразно при изм вх вел-ны
Классификация: 2 группы, 1) элементы, позв создавать комбинац устройства, осн. Св-вом кот явл сохр своего состояния только в момент поступления вх информации 2) элементы памяти, кот позв создавать ус-ва запомин вх воздействие и не изм. Своего состояния после прекращения вх воздействия
Имеют 2 состояния «0» и «1». пассивные – у кот, вых сигнал образ за счет энергии вх Активные – нетолько за счет энергии входн, но и за счет энергии питания . ДУ – совокупность ДЭлем соед между собой .
-
Функции алгебры логики. Понятие базиса. Теорема Поста-Яблонского.
АЛ является разделом математической логики. Функцию f(X1, X2, …, Xn) называют функцией алгебры логики, если она, как и ее переменные, может принимать только два значения: логический 0 и логическую 1. Поскольку реальные ДУ имеют конечное число входов, то мы будем рассматривать функции конечного числа аргументов. Для nдвоичных переменных x1, x2, …, xn существует k = 2n наборов значений переменных и R = 2k различных ФАЛ. Существует множество способов задания ФАЛ. Среди них наиболее известны такие способы, как: 1) табличный; 2) графический; 3) координатный (при помощи карт Карно); 4) числовой; 5) аналитический; 6) на основе диаграмм двоичного решения; 7) при помощи диаграмм Венна; 8) с использованием контактных схемБазисом называют полную систему функций алгебры логики. Система функций является полной, если она включает в себя по крайней мере одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, одну несамодвойственную, одну немонотонную и одну нелинейную функции (теорема Поста ‑ Яблонского).
-
Элементарные ФАЛ и их реализация (на логических элементах, на контактах реле). Под элементарной ФАЛ понимают ф-ю завис от одной или 2-х переменных. Элементарные функции одной или двух переменных реализуются отдельными логическими элементами. Совокупность логических элементов может реализовать различные ФАЛ в зависимости от схемы соединения их между собой. (рисунки И, ИЛИ, НЕ; таблица миним) -
Способы задания ФАЛ: понятие и сравнительные характеристики.
Существует множество способов задания ФАЛ. Среди них наиболее известны такие способы, как: 1) табличный; 2) графический; 3) координатный (при помощи карт Карно); 4) числовой; 5) аналитический; 6) на основе диаграмм двоичного решения; 7) при помощи диаграмм Венна; 8) с использованием контактных схем.
При табл способе ФАЛ задается таблицей зависимости выходных значений от входных наборов. Такая таблица называется таблицей истинности В ТИ каждому набору аргументов соответствует свое значение функции. (таблица ист с f) Графич способ задания ФАЛ основан на сопоставлении наборам значений переменных ФАЛ точек n-мерного пространства. При этом множество наборов 2n определяет число вершин ФАЛ задается единичным квадратом, если она зависит от двух переменных. кубом, если она зависит от трех аргументов При координатном способе ФАЛ задается в виде координатной карты состояний (карты Карно). При числовом способе задания ФАЛ каждому набору переменных ставится в соответствие определенное число в двоичной системе исчисления и присваивается ему соответствующий десятичный номер. Функция задается в виде десятичных номеров, на которых она принимает единичные или нулевые значения. При аналитич способе ФАЛ задается в виде алгебраического выражения, получаемого при применении каких-либо логических операций к переменным. f=x1…
-
Минимальный базис. Теорема о полноте системы ФАЛ (свойства полной системы).
Базисом называют полную систему функций алгебры логики. Минимальный базис состоит из такого набора функций, исключение из которого любой функции превращает этот набор в неполную систему функций. Наиболее удобным для представления в виде логического выражения функций алгебры логики является базис, содержащий конъюнкцию (умножение), дизъюнкцию (сложение) и инверсию (отрицание) (базис И-ИЛИ-НЕ). Этот базис называется основным. Минимальный базис включает в себя две функции И-НЕ (базис Шеффера) либо ИЛИ-НЕ (базис Пирса). Система функций является полной, если она включает в себя по крайней мере одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, одну несамодвойственную, одну немонотонную и одну нелинейную функции (теорема Поста ‑ Яблонского).
-
Канонические формы представления ФАЛ. Получение канонических форм различными способами (по картам Карно, по ТИ). СКНФ – 1 СДНФ – 0
Каноническими формами представления функций алгебры логики являются дизъюнктивная нормальная форма и конъюнктивная нормальная форма
Совершенная дизъюнктивная нормальная форма (СДНФ) представляет собой алгебраическое выражение, которое принимает значение, равное 1 на тех наборах переменных, на которых значение заданной функции равно 1.
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой алгебраическое выражение, которое принимает значение 0 на тех наборах переменных, на которых значение заданной функции равно 0.Канонические формы представления ФАЛ. Переход от ДНФ к СДНФ и от КНФ к СКНФ и наоборот.
Каноническими формами представления функций алгебры логики являются дизъюнктивная нормальная форма и конъюнктивная нормальная форма.
Совершенная дизъюнктивная нормальная форма (СДНФ) представляет собой алгебраическое выражение, которое принимает значение, равное 1 на тех наборах переменных, на которых значение заданной функции равно 1.
Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой алгебраическое выражение, которое принимает значение 0 на тех наборах переменных, на которых значение заданной функции равно 0.
Кроме совершенных форм ФАЛ существуют и простые: дизъюнктивная нормальная форма (ДНФ) и конъюнктивная нормальная форма (КНФ), которые не содержат в своих конституентах всех аргументов. Конституентой единицы (нуля) называют функцию, которая принимает значение единицы (нуля) при одном из всех возможных наборов переменных и нуля (единицы) при всех других.
-
Методы резервирования дискретных устройств. Классификация и сравнение схем резервирования.
Резервирование дискретного устройства предусматривает установку одного или нескольких идентичных экземпляров устройства. Резервироваться может как все устройство в целом, так и отдельные его элементы или блоки. При поблочном резервировании каждый функциональный блок дискретного устройства заменяют несколькими идентичными блоками. Резервирование целиком Ошибки могут быть двух типов: вместо правильного сигнала логического 0 появляется ложный сигнал логической 1 (ошибка типа 01) или вместо правильного сигнала логической 1 – ложный сигнал логического 0 (1 0). Принято также появление сигнала логической 1 вместо логического 0 называть ложным срабатыванием, а появление 0 вместо 1 – ложным несрабатыванием. Схемы резервирования: с использованием мажоритарного элемента (мажоритарный элемент в соответствии со следующим правилом: на выходе мажоритарного элемента присутствует сигнал логической 1 в том и только в том случае, если на большинство его входов поданы сигналы логической 1), – Схема избыточной структуры с несколькими восстанавливающими органами Схема троированной структуры (рисунок)
-
Методы повышения надежности ДУ. Структурное резервирование: классификация методов. + см 8
Резервирование дискретного устройства предусматривает установку одного или нескольких идентичных экземпляров устройства. Резервироваться может как все устройство в целом, так и отдельные его элементы или блоки. При поблочном резервировании каждый функциональный блок дискретного устройства заменяют несколькими идентичными блоками Резервирование целиком Как правило, поблочное резервирование дает большее повышение надежности по сравнению с резервированием всего устройства, но и требует большего числа восстанавливающих органов. Схемы резервирования: с использованием мажоритарного элемента (мажоритарный элемент в соответствии со следующим правилом: на выходе мажоритарного элемента присутствует сигнал логической 1 в том и только в том случае, если на большинство его входов поданы сигналы логической 1), – Схема избыточной структуры с несколькими восстанавливающими органами Схема троированной структуры
-
Делители частоты. Понятие, принципы построения.
Счетчиком называется устройство, подсчитывающее число импульсов и представляющее собой последовательное устройство с одним двоичным входом и определенным числом внутренних состояний, отождествляемых с некоторым числовым кодом В счетчиках используют числовые коды с различными основаниями счета т. Наиболее часто применяют двоичные (т = 2) и десятеричные (т = 10) счетчики, а также восьмеричные (т = 8) и шестнадцатеричные (т = 16). Максимальное число импульсов, которое может сосчитать счетчик, называется коэффициентом (модулем) счета Ксч. Счетчики могут быть одноразрядными, если Ксч не превышает основание счета m, многоразрядными, если Ксч > m.
-
Минимизация ФАЛ. Минимизация при помощи карт Карно.
Функция представляется при помощи карты Карно. При этом для любой клетки карты существует соседняя по строке и столбцу, такая что координаты этой клетки отличаются от координат рассматриваемой клетки значением лишь одной переменной. Это свойство позволяет выполнять на карте минимизацию функций, отображая процесс склеивания соседних конституентов и минтермов, соответствующих клеткам карты, путем построения различных объединений клеток. Минимальные выражения могут быть получены как на основе ДНФ, так и на основе КНФ. Если требуется получить выражение на базе ДНФ, то в карте учитываются клетки с единицами, а если на основе КНФ, то – с нулями. Правила объединения в контуры при минимизации для ДНФ: 1)все единицы должны быть заключены в прямоугольные контуры; 2) во всех клетках контура должны быть только единицы; 3) число клеток в контуре должно быть кратным степени числа два; 4) контуры могут накладываться друг на друга; 5) контуры, все клетки которых уже вошли в другие контуры, являются лишними; 6) для получения наиболее простой формулы надо выбирать контуры с максимально возможным числом клеток; 7) каждому контуру соответствует конъюнкция, составленная из переменных, значения которых не изменяются во всех клетках контура, т.е. конъюнкций будет столько, сколько в карте контуров.
-
Минимизация ФАЛ. Минимизация методом Квайна.
Метод Квайна имеет четко сформулированный алгоритм осуществления отдельных операций. Для проведения минимизации этим методом требуется достаточно много времени ввиду необходимости попарного сравнения друг с другом каждого члена логической функции. При минимизации по методу Квайна предполагается, что исходная функция задана в СДНФ. Суть метода в следующем.
1 Осуществляется переход от канонической формы записи ФАЛ (СДНФ) к сокращенной на основе формулы склеивания
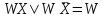 , где W – одинаковая часть выражения в обеих конъюнкциях формулы, Х – переменная, которая в разных конъюнкциях имеет противоположные значения.
, где W – одинаковая часть выражения в обеих конъюнкциях формулы, Х – переменная, которая в разных конъюнкциях имеет противоположные значения.2 Выполняется переход от сокращенной формы ФАЛ к минимальной с применением формулы поглощения
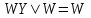 , где Y – часть конъюнкции, которая в одной конъюнкции присутствует, а в другой отсутствует.
, где Y – часть конъюнкции, которая в одной конъюнкции присутствует, а в другой отсутствует.-
Минимизация ФАЛ. Метод существенных переменных.
Метод существенных переменных основан на сопоставлении разрешенных наборов значений переменных, на которых ФАЛ принимает единичное значение, с запрещенными наборами, на которых ФАЛ принимает нулевое значение. В том случае, если хотя бы на одном наборе переменных выполняется неравенство
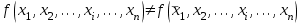 , переменная xi является существенной. При минимизации неполностью заданных функций методом существенных переменных необходимо пройти следующие пять этапов [1].
, переменная xi является существенной. При минимизации неполностью заданных функций методом существенных переменных необходимо пройти следующие пять этапов [1].1-й этап. Построение таблицы существенных переменных. Таблица должна содержать n строк – по числу разрешенных наборов функции, mстолбцов – по числу запрещенных наборов и столбец остатков, в который записываются существенные переменные по результатам сравнения разрешенных наборов строк с запрещенными наборами столбцов.
2-й этап. Заполнение таблицы существенных переменных. Для этого попарно сравнивают разрешенный набор строки с каждым запрещенным набором столбца. В клетку таблицы заносятся те переменные, по которым рассматриваемая пара наборов различается между собой, и с теми значениями, которые переменные имеют в разрешенном наборе.
3-й этап. Обработка таблицы существенных переменных. Она проводится построчно в следующем порядке:
а) определяются те клетки, которые содержат по одной переменной. Эти переменные обводятся кружком и записываются в столбец остатков в виде конъюнкции. Все члены строки, которые содержат переменные, записанные в столбец остатков, отмечаются знаком дизъюнкции «» и исключаются из рассмотрения;
б) среди членов строки, не отмеченных знаком «», выделяется переменная, встречающаяся наиболее часто. Она обводится кружком и приписывается со знаком конъюнкции в столбец остатков к имеющимся там переменным. Члены строки, содержащие данную переменную, отмечаются знаком «» и исключаются из рассмотрения. Этот процесс продолжается до тех пор, пока в строке останутся неотмеченными только клетки, содержащие неповторяющиеся переменные или переменные, повторяющиеся одинаковое число раз;
в) оставшиеся неотмеченными неповторяющиеся переменные или повторяющиеся одинаковое число раз соединяются знаком дизъюнкции, заключаются в скобки и через знак конъюнкции приписываются в столбец остатков к имеющимся там существенным переменным.
4-й этап. Построение таблицы покрытий существенных переменных. Эта таблица аналогична импликантной таблице в методе Квайна. Ее столбцы соответствуют разрешенным наборам, а строки – конъюнкциям существенных переменных, полученных для каждой строки таблицы существенных переменных. Если одним из членов конъюнкции в столбце остатков является дизъюнкция переменных, то осуществляется преобразование по распределительному закону (раскрываются скобки).
5-й этап. Обработка таблицы покрытий. Обработка выполняется, как и обработка импликантной таблицы: проставляются отметки в тех столбцах таблицы, наборы которых покрываются данной комбинацией существенных переменных, т.е. эта комбинация образована в результате сравнения соответствующего разрешенного набора с запрещенными наборами.
-
Опасные состязания в комбинационных схемах. Способы исключения
Ситуации, когда из-за неодновременного срабатывания триггеров, вызванного выше указанными причинами автомат отказывается в непредусмотренные состояния al вместо as и под действием присутствующего на входе сигнала Zk переходит в новое состояние, наз. состязаниями.
Состязания:
1)Критические (гонки)- состязания, когда из непредусмотренного состояния мы переходим далее по графу и не попадаем в состояние as.
2)Не критические —состязания, в результате которых автомат всё таки оказывается в нужном состоянии as после изменения состояния последнего из самых медленных триггеров.
Меры по устранению гонок в структурном автомате:
1)Направленное кодирование состояний абстрактного автомата(Превращение критических состояний в некритические).
2) Cоседние кодирование соседних состояний.
3)Синхронизация структурного автомата.
4)Двойная память.
-
Минимизация ФАЛ. Минимизация методом Квайна — Мак-Класки. См 12
Суть метода в следующем. Члены СДНФ записываются в виде их двоичных номеров. Все номера разбиваются на группы по числу единиц в них. При этом в i-ю группу входят все номера, которые имеют в своем двоичном коде количество единиц равное i. Затем выполняется попарное сравнение членов соседних по номеру групп (т.е. реализуется закон склеивания по отношению к кодовым комбинациям), так как только члены этих групп отличаются лишь в одном разряде. При образовании членов с рангом (числом единиц) выше нулевого в разряды, соответствующие исключенным переменным, пишется знак тире (прочерк). В остальном методика не отличается от метода Квайна.
-
Синхронные конечные автоматы. Особенности синтеза. Сравнение с асинхронными конечными автоматами.
Синхронный автомат - конечный автомат, в котором:
- генератор тактовых импульсов воздействует на автомат;
- выходные сигналы считываются только во время выдачи тактовых импульсов, когда под воздействием входных и промежуточных сигналов автомат уже перешел в новое состояние.
В синхронных конечных автоматах моменты времени, в которые автомат считывает входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учётом «считанного» и в соответствии с соотношениями для функционирования автомата происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала.
Асинхронный конечный автомат считывает входной сигнал непрерывно, и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины x, он может, как следует из соотношений для функционирования автомата, несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдёт в устойчивое состояние, которое уже не может быть изменено данным входным сигналом.
-
Минимизация неполностью заданных ФАЛ. Метод Квайна для неполностью заданных ФАЛ.
При упрощении неполностью заданных ФАЛ методами Квайна и Квайна – Мак-Класки необходимо выполнить следующие этапы.
1 Из частично заданной функции f получить полностью заданную функцию f0 посредством замены на нуль безразличных состояний функции f.
2 Из той же частично заданной функции f получить новую полностью заданную функцию f1 путем замены на единицу безразличных состояний функции f.
3 Упростить функцию f1 обычным путем (как это описано в пп. 4.2.3 или 4.2.4 данного пособия).
4 Составить таблицу перекрытий между элементарными конъюнкциями функции f0 и упрощенной функции f1 и по этой таблице выбрать окончательную минимальную форму частично заданной функции f .
-
Критические состязания элементов памяти. Способы исключения критических состязаний.
Критические (гонки)- состязания, когда из непредусмотренного состояния мы переходим далее по графу и не попадаем в состояние as.
Меры по устранению гонок в структурном автомате:
1)Направленное кодирование состояний абстрактного автомата(Превращение критических состояний в некритические).
2) Cоседние кодирование соседних состояний.
3)Синхронизация структурного автомата.
4)Двойная память.
-
Минимизация неполностью заданных ФАЛ. Метод Квайна–Мак-Класки для неполностью заданных ФАЛ.
При упрощении неполностью заданных ФАЛ методами Квайна и Квайна – Мак-Класки необходимо выполнить следующие этапы.
1 Из частично заданной функции f получить полностью заданную функцию f0 посредством замены на нуль безразличных состояний функции f.
2 Из той же частично заданной функции f получить новую полностью заданную функцию f1 путем замены на единицу безразличных состояний функции f.
3 Упростить функцию f1 обычным путем (как это описано в пп. 4.2.3 или 4.2.4 данного пособия).
4 Составить таблицу перекрытий между элементарными конъюнкциями функции f0 и упрощенной функции f1 и по этой таблице выбрать окончательную минимальную форму частично заданной функции f .
-
Состязания в комбинационных схемах. Опасные состязания в комбинационных схемах.
Ситуации, когда из-за неодновременного срабатывания триггеров, вызванного выше указанными причинами автомат отказывается в непредусмотренные состояния al вместо as и под действием присутствующего на входе сигнала Zk переходит в новое состояние, наз. состязаниями.
Состязания:
1)Критические (гонки)- состязания, когда из непредусмотренного состояния мы переходим далее по графу и не попадаем в состояние as.
2)Не критические —состязания, в результате которых автомат всё таки оказывается в нужном состоянии as после изменения состояния последнего из самых медленных триггеров.
-
Состязания элементов памяти. Критические состязания элементов памяти и их исключение.
Ситуации, когда из-за неодновременного срабатывания триггеров, вызванного выше указанными причинами автомат отказывается в непредусмотренные состояния al вместо as и под действием присутствующего на входе сигнала Zk переходит в новое состояние, наз. состязаниями.
Критические (гонки)- состязания, когда из непредусмотренного состояния мы переходим далее по графу и не попадаем в состояние as.
Меры по устранению гонок в структурном автомате:
1)Направленное кодирование состояний абстрактного автомата(Превращение критических состояний в некритические).
2) Cоседние кодирование соседних состояний.
3)Синхронизация структурного автомата.
4)Двойная память
-
Синтез ФАЛ в различных базисах. Реализация ФАЛ в базисе И-НЕ.
Для того, чтобы вып синтез уст-ва необходимо соблюдения правил: 1) логические функйии должны быть представлены в виде формулылы с обозначением базиса 2) При анализе логич функции использовать свой элемент Рисунок элемента Шеффера. Используется правило Де-Моргана и операции двойного инвертирования, исп. Переместительный закон x1|x2|x3 x1|x3|x2
-
Конечные автоматы. Графический метод синтеза. Этапы синтеза.
Конечный автомат - математическая модель устройства с конечной памятью. Конечный автомат перерабатывает множество входных дискретных сигналов в множество выходных сигналов. Различают синхронные и асинхронные конечные автоматы.
Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.
-
Синтез ФАЛ в различных базисах. Реализация ФАЛ в базисе ИЛИ-НЕ. Нарисовать от руки
Для того, чтобы вып синтез уст-ва необходимо соблюдения правил: 1) логические функйии должны быть представлены в виде формулылы с обозначением базиса 2) При анализе логич функции использовать свой элемент
-
Разложение булевых функций. Методы упрощения контактных схем.
1) Формула разложения: любую булевую функцию
Если последовательно какой-либо контактной схемы вкл. одиночный контакт реле, то все одноименные по действию контакты этого реле, задействованные в схеме, можно закоротить, а все разноименные исключить из схемы
2) Ф-ла упрощения: Если последовательно какой-либо контактной схемы вкл. одиночный контакт реле, то все одноименные по действию контакты этого реле, задействованные в схеме, можно исключить, а все разноименные – закоротить.
-
Конечные автоматы. Классификация.
Конечный автомат - математическая модель устройства с конечной памятью. Конечный автомат перерабатывает множество входных дискретных сигналов в множество выходных сигналов. По способу формирования функций выходов бывают автоматы Мили и Мура.
Асинхронный автомат - конечный автомат, в котором выходные сигналы считываются в любое время, а переход в новое состояние определяется лишь временем срабатывания всех логических элементов, входящих в логический преобразователь.
Синхронный автомат - конечный автомат, в котором:
- генератор тактовых импульсов воздействует на автомат;
- выходные сигналы считываются только во время выдачи тактовых импульсов, когда под воздействием входных и промежуточных сигналов автомат уже перешел в новое состояние.
-
Шифраторы, дешифраторы, преобразователи кодов: назначение, реализации.
Шифратором (кодером) называется устройство, преобразующее сигнал логической 1 на одном из входов в соответствующую кодовую комбинацию на выходах. Шифраторы используют, например, для ввода информации в цифровые системы. Дешифратором (декодером) называется устройство, распознающее различные кодовые комбинации, т. е. преобразующее двоичное число в сигнал логической единицы на одном из выходов, соответствующем десятичной цифре поданной на вход двоичной комбинации. Число входов дешифратора определяется числом символов кодовой комбинации n, а число выходов m = 2n. Дешифраторы по принципу построения делятся на одноступенчатые (линейные) и многоступенчатые. Преобразователем кодов (кодопреобразователем) называется устройство для преобразования одного вида двоичного кода в другой. Преобразование одного кода в другой можно осуществлять последовательным соединением дешифратора и шифратора.
-
Конечные автоматы. Классификация.
Конечный автомат - математическая модель устройства с конечной памятью. Конечный автомат перерабатывает множество входных дискретных сигналов в множество выходных сигналов. По способу формирования функций выходов бывают автоматы Мили и Мура.
Асинхронный автомат - конечный автомат, в котором выходные сигналы считываются в любое время, а переход в новое состояние определяется лишь временем срабатывания всех логических элементов, входящих в логический преобразователь.
Синхронный автомат - конечный автомат, в котором:
- генератор тактовых импульсов воздействует на автомат;
- выходные сигналы считываются только во время выдачи тактовых импульсов, когда под воздействием входных и промежуточных сигналов автомат уже перешел в новое состояние.
-
Конечные автоматы. Описание и способы задания.
Конечный автомат - математическая модель устройства с конечной памятью. Конечный автомат перерабатывает множество входных дискретных сигналов в множество выходных сигналов. Различают синхронные и асинхронные конечные автоматы. По способу формирования функций выходов бывают автоматы Мили и Мура.
Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, дуги — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой должны быть надписаны все они.
Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.
-
Регистры. Последовательно-параллельные регистры: пример реализации и принцип действия Регистрами называются устройства, выполняющие функции приема, хранения, логической обработки и передачи информации. Информация в регистре хранится в виде числа (слова), представленного комбинацией сигналов "0" и "1". Каждому разряду числа, записываемому в регистр, соответствует свой разряд регистра В регистре могут выполняться следующие основные операции над n-разрядным входным кодом х1, x2, x3, ..., хn: а) предварительная установка регистра; б) прием и хранение кода числа х1, x2, x3, ..., хn из другого устройства; в) передача кода числа из регистра в другое устройство (в сумматор, в запоминающее устройство, в другой регистр и т. д.); г) сдвиг хранимого в регистре кода на один или несколько разрядов вправо или влево; д) преобразование последовательного кода в параллельный и наоборот; е) поразрядные логические операции. Классифицируются регистры по способу приема и выдачи кода числа (параллельные, последовательные, параллельно-последовательные), по количеству каналов передачи информации (парафазные и однофазные), по способу тактирования (однотактного и многотактного действия).
Для приема любого кода числа х1, х2, х3, ..., хn и его выдачи применяются системы входных и выходных логических схем.
На рисунке 2.3 приведена функциональная схема регистра на асинхронных RS-триггерах, которая позволяет принимать числа, заданные в параллельном коде потенциальными однофазными сигналами, поступающими на входы системы входных схем "И", и осуществлять выдачу этого числа или с выходов Q (прямой код числа), или с выходов
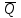 (инверсный код) с помощью элементов 2И-ИЛИ.
(инверсный код) с помощью элементов 2И-ИЛИ.После подачи сигнала У1 триггеры регистра устанавливаются в состояние 000. Поданный на шину приема числа импульсный сигнал У2проходит на единичные (S) входы триггеров регистра только в тех разрядах, где хi = 1. Если код числа х1, x2, х3 задан в виде импульсных сигналов, то необходима синхронизация передачи сигналов информационного кода и сигнала приема кода. При использовании синхронных RS-триггеров входные логические элементы И исключаются, а функции сигнала У2выполняет синхросигнал, подаваемый в триггер. Функциональная схема регистра на синхронных RS-триггерах приведена на рисунке 2.1. Здесь прием информации в регистр осуществляется в парафазном коде (х1,
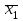 ; x2,
; x2, 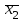 ; x3,
; x3,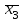 ) без предварительной установки и за один такт. При этом на S-вход каждого триггера подается код данного разряда числа (хi), на вход R– его инверсия (
) без предварительной установки и за один такт. При этом на S-вход каждого триггера подается код данного разряда числа (хi), на вход R– его инверсия (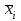 ).
).Выдача числа из регистра может осуществляться как в прямом, так и в инверсном коде. С прямых выходов триггеров регистра снимается прямой код, с инверсных – инверсный. При парафазной выдаче числа используются одновременно оба выхода каждого триггера, при однофазной – только один из них. Так, в схеме, представленной на рисунке 2.3 длявыдачи информации в прямом коде используется сигнал У3, а в инверсном – У4. При парафазной выдаче прямого и инверсного кодов используются две схемы 2И-ИЛИ на один разряд.
-
Регистры. Параллельно-последовательные регистры: пример реализации и принцип действия.