Файл: Дискретные элементы и дискретные устройства понятия, свойства, класся Элемент.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 55

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Совершенная конъюнктивная нормальная форма (СКНФ) представляет собой алгебраическое выражение, которое принимает значение 0 на тех наборах переменных, на которых значение заданной функции равно 0.

Кроме совершенных форм ФАЛ существуют и простые: дизъюнктивная нормальная форма (ДНФ) и конъюнктивная нормальная форма (КНФ), которые не содержат в своих конституентах всех аргументов. Конституентой единицы (нуля) называют функцию, которая принимает значение единицы (нуля) при одном из всех возможных наборов переменных и нуля (единицы) при всех других.

  1. Теорема о полноте системы ФАЛ. Формулировка, пояснения на примерах. Понятие базиса.

Функцию f(X1, X2, …, Xn) называют функцией алгебры логики, если она, как и ее переменные, может принимать только два значения: логический 0 и логическую 1. Система функций является полной, если она включает в себя по крайней мере одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, одну несамодвойственную, одну немонотонную и одну нелинейную функции (теорема Поста ‑ Яблонского). Свойством сохранения нуля функция f(X1, X2, …, Xn) обладает, если она на нулевом наборе аргументов равна нулю, т.е. f(0,0,…,0)=0.

Свойством сохранения единицы функция f(X1, X2, …, Xn) обладает, если она на единичном наборе аргументов равна единице, т. е. f(1, 1,…, 1) = 1.

Свойством самодвойственности обладает функция, у которой инвертирование всех аргументов приводит к инверсии значения функции, т.е. .

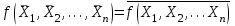Свойством монотонности обладает функция, значение которой при любом возрастании набора не убывает, т. е.



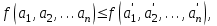
где .

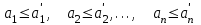Свойством линейности обладает функция, которая может быть представлена полиномом первой степени:



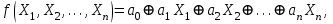
где a0, a1, …, an – коэффициенты, равные нулю или единице.

Базисом называют
полную систему функций алгебры логики. Минимальный базис состоит из такого набора функций, исключение из которого любой функции превращает этот набор в неполную систему функций.

  1. Триггеры: структура, принципы построения, классификация.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. В случае необходимости входным сигналом триггер переводится из одного устойчивого состояния в другое, тем самым изменяется записанная в нем информация.

Наибольшее распространение получили статические (потенциальные) триггеры, в которых устойчивые состояния различаются уровнем постоянного потенциала. Основу статических триггеров составляет бистабильная ячейка на двух логических элементах ИЛИ-НЕ или И-НЕ, охваченных перекрестной положительной обратной связью. Выходные сигналы в триггере взаимно инверсны (противоположны в логическом смысле). Один выход называют прямым, а другой – инверсным. По способу управления триггеры бывают со статическим (срабатывают в момент, когда входной сигнал достигает порогового уровня) и динамическим (реагируют на перепад управляющего сигнала) управлением. По способу ввода информации триггеры подразделяют на асинхронные (ввод информации определяется изменением сигналов на логических входах) и синхронные (смены информационных сигналов еще не достаточно для их переключения – нужен дополнительный командный импульс). Основным и наиболее общим классификационным признаком является функциональный, который позволяет подразделять триггеры по их функциональному назначению и числу входов. Описание работы триггера задается в виде таблицы переходов (состояний), определяющей состояние триггера Qn+1 в момент времениtn+1, если известно его состояние Qn и значение входного сигнала Xn в момент времени tn. При одном входе возможны только два значения входного сигнала и две имеющие практическое значение таблицы состояний

  1. Сумматоры: понятие, классификация, принципы построения.

Двоичные сумматоры выполняют арифметическую операцию сложения двоичных чисел по модулю два ().Существует два вида сумматоров: с параллельным и последовательным действием. У сумматоров с параллельным действием сложение выполняется параллельно, сразу во всех разрядах суммируемых чисел. В сумматорах с последовательным действием имеется только одна одноразрядная суммирующая схема и результат образуется последовательным сложением отдельных разрядов. Таблица истинности такого сумматора для i-го разряда содержит три двоичных входа: аi – первое слагаемое, bi – второе слагаемое и pi–1 – перенос из i1 разряда в i-й. В результате сложения этих трех двоичных чисел образуется двухразрядное число, поэтому сумматор должен иметь два двоичных выхода. Младший выход si результата сложения называется частичной суммой, а старший выход pi – переносом.

Исходя из таблицы истинности, запишем функции выходов si и pi:





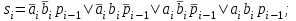
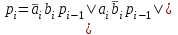
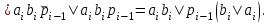
  1. Сумматоры: двоично-десятичный сумматор.

Двоичные сумматоры выполняют арифметическую операцию сложения двоичных чисел по модулю два ().Существует два вида сумматоров: с параллельным и последовательным действием. У сумматоров с параллельным действием сложение выполняется параллельно, сразу во всех разрядах суммируемых чисел. В сумматорах с последовательным действием имеется только одна одноразрядная суммирующая схема и результат образуется последовательным сложением отдельных разрядов.

  1. Реализация схем вычитания на сумматорах.

Двоичные сумматоры выполняют арифметическую операцию сложения двоичных чисел по модулю два (). Последовательный сумматор для сложения одновременно трех слагаемых в дополнительном коде, разряды которых подаются на входы сумматора один за другим, показан на рисунке 2.6. Схема состоит из двух комбинационных одноразрядных сумматоров SM1и SM2 и двух триггеров Т1 и Т2. Сумматор SM1 и триггер Т1 образуют последовательный сумматор для сложения первых двух слагаемых, i-e разряды которых обозначены 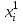и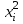 . Сумматор SM2и триггер T2 образуют последовательный сумматор для сложения суммы первых двух слагаемых и третьего слагаемого, i-е разряды которых обозначены 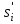и .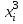

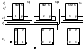
Схема сумматора для сложения четырех разрядов двоичного числа

Входы
Выходы

ai
bi
pi-1
si
pi

0
0
0
0
0

0
0
1
1
0

0
1
0
1
0

0
1
1
0
1

1
0
0
1
0

1
0
1
0
1

1
1
0
0
1

1
1
1
1
1



  1. Динамические триггеры. Особенности включения и функционирования.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. Входы делятся на статические и динамические. Динамические прямые и инверсные входы – соответственно указателями  и .

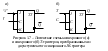
  1. Статические триггеры. Схемы, особенности функционирования.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. Входы делятся на статические и динамические. Инверсные статические входы и выходы триггера обозначают символом логического отрицания 

  1. Т-триггеры. Получение Т-триггеров на основе триггеров других типов.

Триггер представляет собой устройство с двумя устойчивыми состояниями: 0 и 1. Он удобен для обработки двоичной информации. Двум устойчивым состояниям триггера отвечают различные значения выходного сигнала, каждый из которых соответствует логическим 0 и 1. Записанная в триггере двоичная информация (0 или 1) сохраняется до тех пор, пока состояние триггера не изменится. Счетный триггер (Т-триггер) является частным случаем JK-триггера, когда при соединении входов выполняется соотношение К = J. Поэтому Т-триггеры также склонны к генерации и могут быть реализованы как триггеры с динамическим управлением или двухступенчатой структурой. В виде самостоятельных изделий T-триггеры не выпускают, их получают из триггеров других типов.

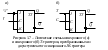
– Логические схемы Т-триггеров, преобразованных из D-триггера с динамическим управлением (а) и двухступенчатого RS-триггера (б)


  1. Счетчики импульсов: понятие, классификация, принципы построения и функционирования. (3 стр5)

Счетчиком называется устройство, подсчитывающее число импульсов и представляющее собой последовательное устройство с одним двоичным входом и определенным числом внутренних состояний, отождествляемых с некоторым числовым кодом. В счетчиках используют числовые коды с различными основаниями счета т. Наиболее часто применяют двоичные (т = 2) и десятеричные (т = 10) счетчики, а также восьмеричные (т = 8) и шестнадцатеричные (т = 16). Максимальное число импульсов, которое может сосчитать счетчик, называется коэффициентом (модулем) счета Ксч. Счетчики могут быть одноразрядными, если Ксч не превышает основание счета m, многоразрядными, если Ксч > m. В многоразрядном счетчике выходное слово будет представлять n-разрядное число, где п – число разрядов счетчика. В счетчиках статического типа состояния изображаются потенциалами на его выходах, число которых равно числу состояний. Состояние каждого разряда может отображаться логической единицей (прямые выходы) или логическим нулем (инверсные выходы) на соответствующем выходе. На остальных выходах должны быть логические инверсные значения. Импульсы считаются как в направлении увеличения, так и в направлении уменьшения числового кода. По направлению счета счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующем счетчике каждый очередной импульс на входе увеличивает значение кода на единицу, а в вычитающем счетчике – уменьшает на единицу. Реверсивный счетчик может работать как суммирующий или как вычитающий счетчик в зависимости от управляющих сигналов, определяющих направление счета.

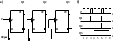Схема построения на Т-триггерах
на D-триггерах

Для перехода к вычитающему счетчику достаточно в цепи переноса заменить инвертирующий выход прямым

  1. Счетчики. Классификация. Синтез счетчиков с последовательным переносом.

Счетчиком называется устройство, подсчитывающее число импульсов и представляющее собой последовательное устройство с одним двоичным входом и определенным числом внутренних состояний, отождествляемых с некоторым числовым кодом. В счетчиках используют числовые коды с различными основаниями счета т. Наиболее часто применяют двоичные (т = 2) и десятеричные (т = 10) счетчики, а также восьмеричные (т = 8) и шестнадцатеричные (т = 16). Максимальное число импульсов, которое может сосчитать счетчик, называется коэффициентом (модулем) счета Ксч. Счетчики могут быть одноразрядными, если Ксч не превышает основание счета m, многоразрядными, если Ксч > m. В многоразрядном счетчике выходное слово будет представлять n-разрядное число, где п – число разрядов счетчика. В счетчиках статического типа состояния изображаются потенциалами на его выходах, число которых равно числу состояний. Состояние каждого разряда может отображаться логической единицей (прямые выходы) или логическим нулем (инверсные выходы) на соответствующем выходе. На остальных выходах должны быть логические инверсные значения. Импульсы считаются как в направлении увеличения, так и в направлении уменьшения числового кода. По направлению счета счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующем счетчике каждый очередной импульс на входе увеличивает значение кода на единицу, а в вычитающем счетчике – уменьшает на единицу. Реверсивный счетчик может работать как суммирующий или как вычитающий счетчик в зависимости от управляющих сигналов, определяющих направление счета. В счетчиках с последовательным переносом триггер i-гo разряда переключается выходным сигналом триггера (i  1)-го разряда счетчика. В счетчиках с параллельным переносом для формирования сигналов переноса в схему вводят конъюнктуры. На все триггеры счетчика одновременно воздействуют входной (счетный) сигнал и сигналы с выходов других триггеров. последовательным (а) и параллельным (б) переносами



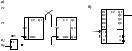
  1. Счетчики. Классификация. Синтез счетчиков с параллельным переносом.

Счетчиком называется устройство, подсчитывающее число импульсов и представляющее собой последовательное устройство с одним двоичным входом и определенным числом внутренних состояний, отождествляемых с некоторым числовым кодом. В счетчиках используют числовые коды с различными основаниями счета т. Наиболее часто применяют двоичные (т = 2) и десятеричные (т = 10) счетчики, а также восьмеричные (т = 8) и шестнадцатеричные (т = 16). Максимальное число импульсов, которое может сосчитать счетчик, называется коэффициентом (модулем) счета Ксч. Счетчики могут быть одноразрядными, если Ксч не превышает основание счета m, многоразрядными, если Ксч > m. В многоразрядном счетчике выходное слово будет представлять n-разрядное число, где п – число разрядов счетчика. В счетчиках статического типа состояния изображаются потенциалами на его выходах, число которых равно числу состояний. Состояние каждого разряда может отображаться логической единицей (прямые выходы) или логическим нулем (инверсные выходы) на соответствующем выходе. На остальных выходах должны быть логические инверсные значения. Импульсы считаются как в направлении увеличения, так и в направлении уменьшения числового кода. По направлению счета счетчики делятся на суммирующие, вычитающие и реверсивные. В суммирующем счетчике каждый очередной импульс на входе увеличивает значение кода на единицу, а в вычитающем счетчике – уменьшает на единицу. Реверсивный счетчик может работать как суммирующий или как вычитающий счетчик в зависимости от управляющих сигналов, определяющих направление счета. В счетчиках с последовательным переносом триггер i-гo разряда переключается выходным сигналом триггера (i  1)-го разряда счетчика. В счетчиках с параллельным переносом для формирования сигналов переноса в схему вводят конъюнктуры. На все триггеры счетчика одновременно воздействуют входной (счетный) сигнал и сигналы с выходов других триггеров. последовательным (а) и параллельным (б) переносами

Смотрите также файлы