Файл: Практическая работа 6 и 7 уравнение состояния идеального газа и Изопроцессы на графике.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 569
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 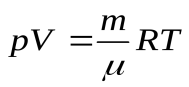 . (17.2)
. (17.2)
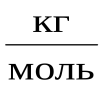
где R = 8,31 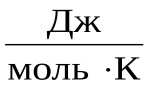 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
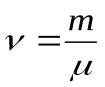 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 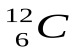 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 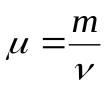
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
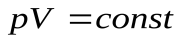 или
или 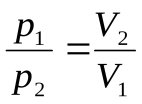 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н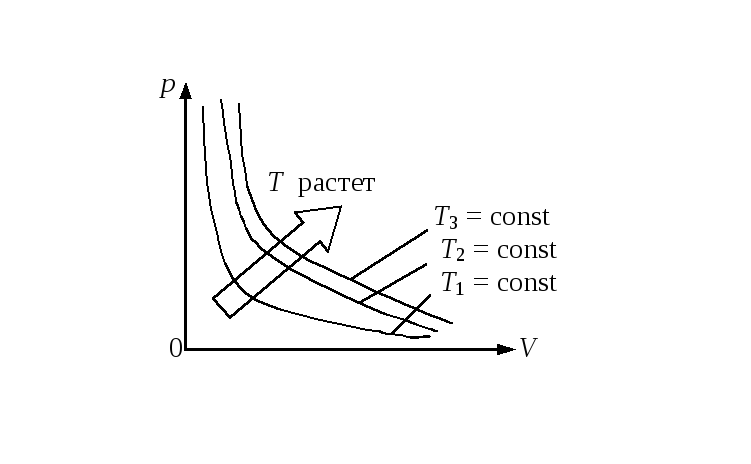 азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
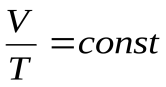 или
или 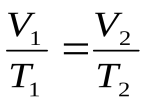 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р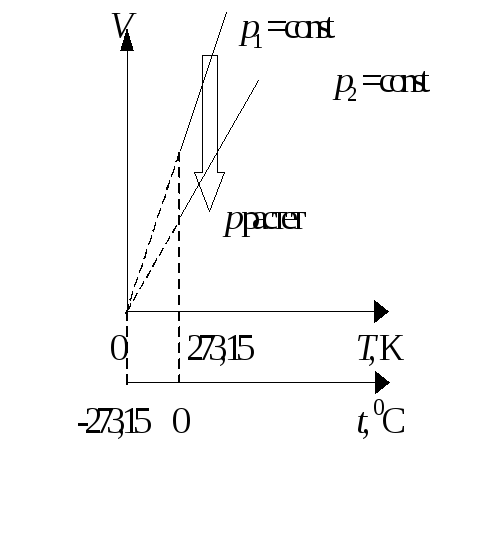 ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
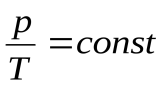 или
или 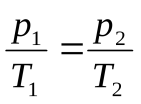 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н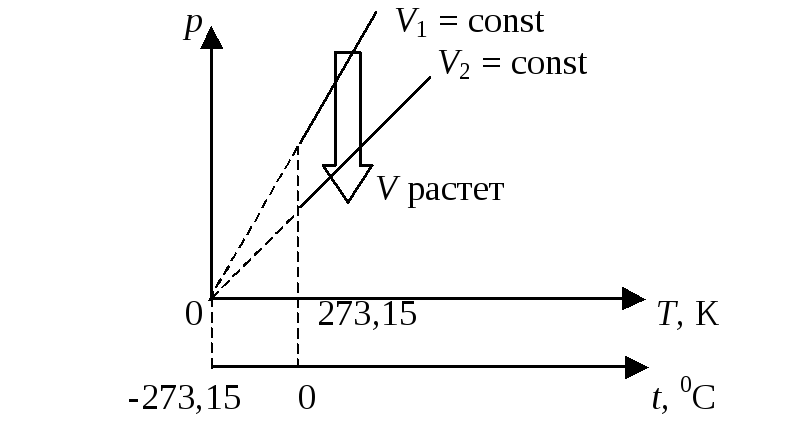 азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 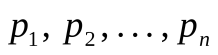 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 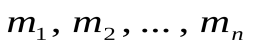 и молярными массами
и молярными массами 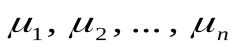 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,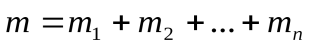 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
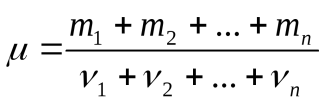 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (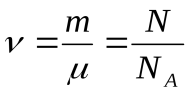 )
)
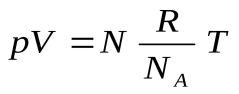 , (17.10)
, (17.10)
где 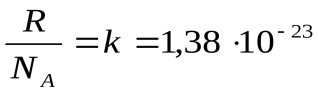
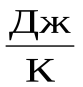 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 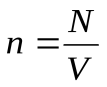 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г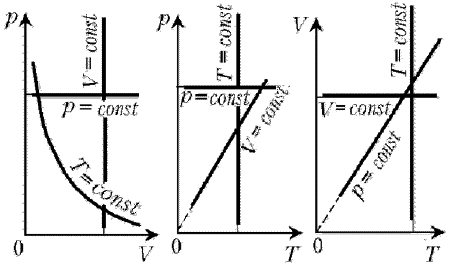 рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П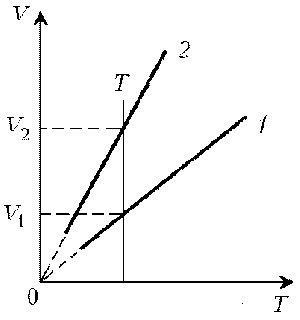 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П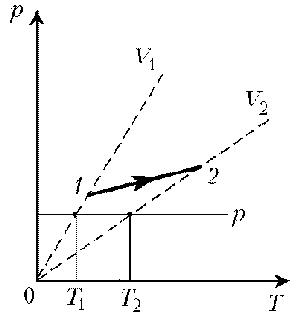 ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П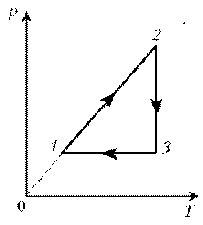 ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1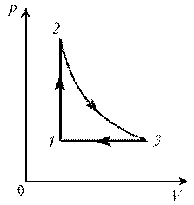 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П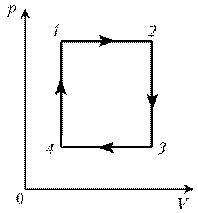 ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1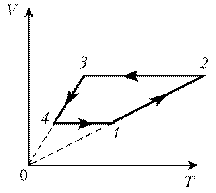 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П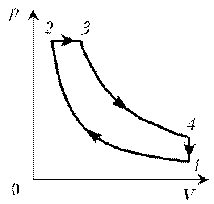 ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2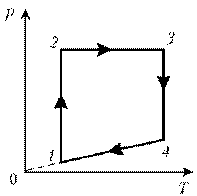 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П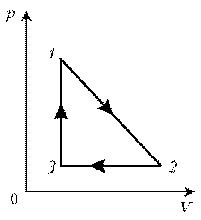 ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1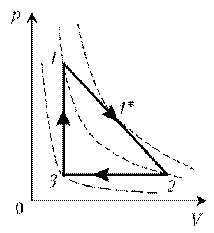 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П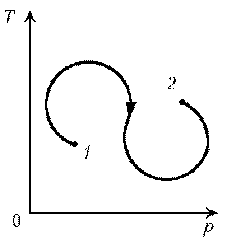 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и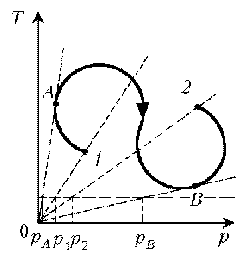 зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П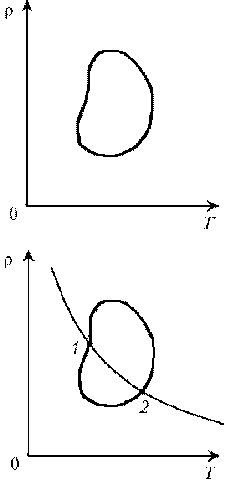 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
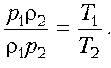
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П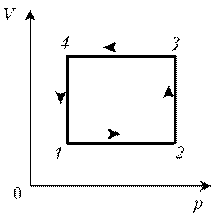 ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
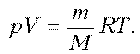
П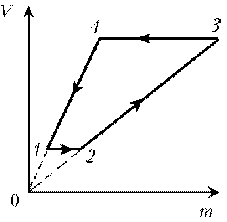 о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
-
П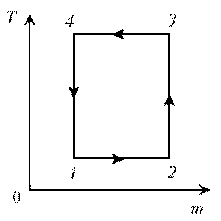 ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева: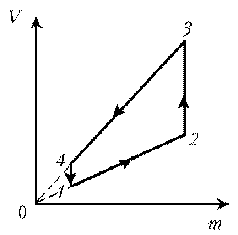
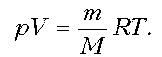
1–2: р = const; T = const; V
m; m; V.
2–3: р = const; m = const; V
T; T; V.
3–4: р = const; T = const; V
m; m; V
4–1: р = const; m = const; V
T; T; V.
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
-
П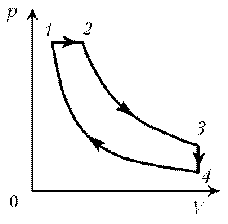 ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .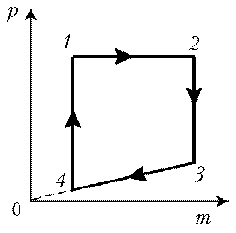
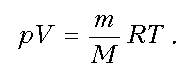
1–2: T = const, р = const; V
m; V; m
2–3: T = const, р
1/V; m = const; р
3–4: T = const, V = const; р
m; p; m
4–1: T = const, р
1/V; m = const; р
ЗАДАЧИ ПО ИЗОПРОЦЕССАМ
Изо- - значит, неизменный, равный. Изопроцесс - это такой процесс, который производят с газом либо при неизменной температуре, либо при неизменном давлении, либо при неизменном объеме. При этом газ подчиняется уравнению состояния идеального газа, которое превращается в каждом процессе либо в закон Бойля-Мариотта, либо в закон Гей-Люссака, либо в закон Шарля, в зависимости от того, какая величина сохраняет свое значение.
Примеры решения задач
Задача 1. График перехода газа из состояния 1 в состояние 2 в координатах р, Т изображен на рис. 17.4. Как изменился при этом объем газа, если масса газа не изменилась?
Р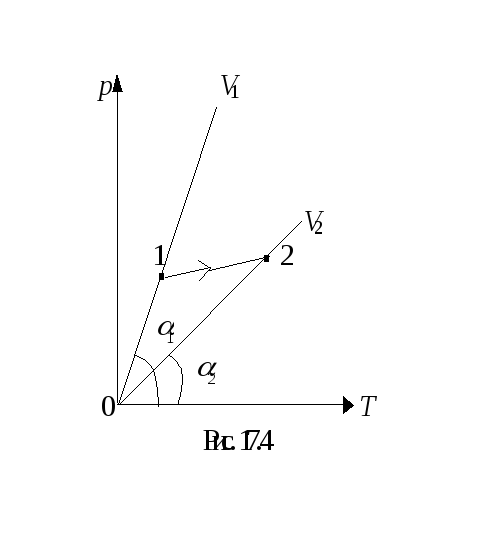 ешение
ешение
Проведем через точки 1 и 2 две изохоры (рис.17.4). Одна изохора соответствует объему V1, другая – V2. Из рис.17.4 видно, что углы наклона изохор 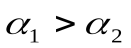 .
.
Тогда
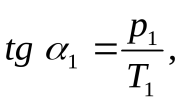 а
а 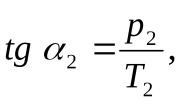
а так как
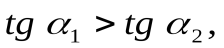
то
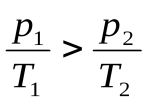 . (1)
. (1)
Из уравнения Менделеева - Клапейрона найдем
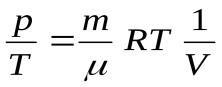 ,
,
т.е.
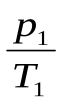
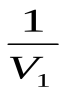 ,
,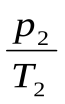
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 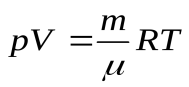 . (17.2)
. (17.2)
где R = 8,31 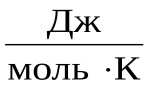 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
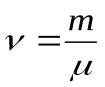 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 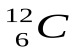 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 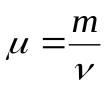
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
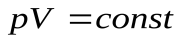 или
или 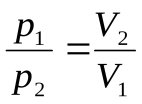 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
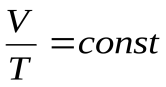 или
или 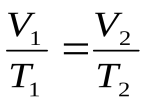 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
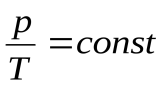 или
или 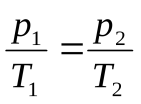 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 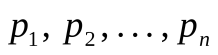 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 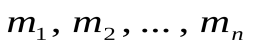 и молярными массами
и молярными массами 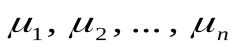 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,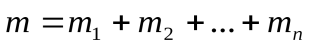 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
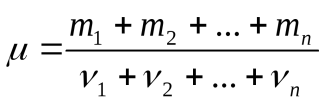 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (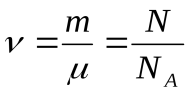 )
)
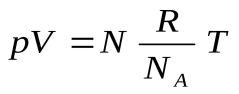 , (17.10)
, (17.10)
где 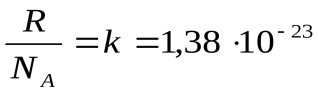
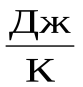 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 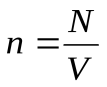 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П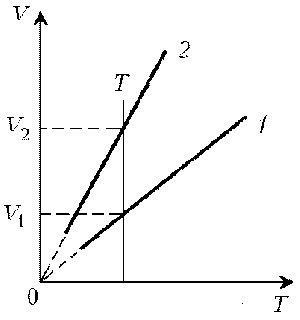 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П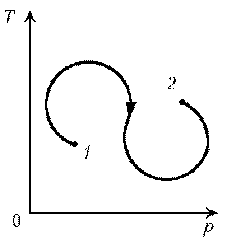 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П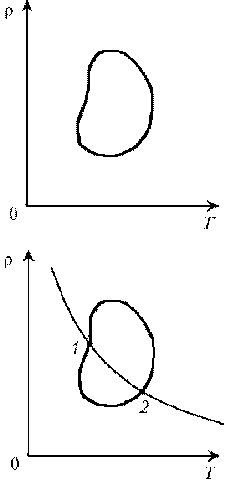 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
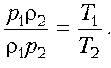
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
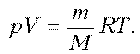
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
-
П ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
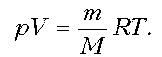
1–2: р = const; T = const; V
m; m; V.
2–3: р = const; m = const; V
T; T; V.
3–4: р = const; T = const; V
m; m; V
4–1: р = const; m = const; V
T; T; V.
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
-
П ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .
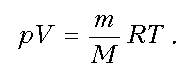
1–2: T = const, р = const; V
m; V; m
2–3: T = const, р
1/V; m = const; р
3–4: T = const, V = const; р
m; p; m
4–1: T = const, р
1/V; m = const; р
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 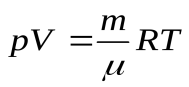 . (17.2)
. (17.2)
где R = 8,31 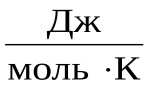 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
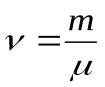 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 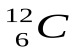 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 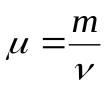
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
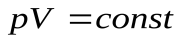 или
или 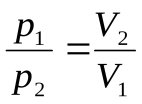 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
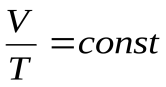 или
или 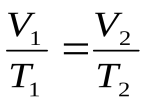 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
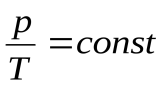 или
или 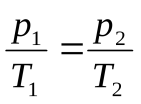 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 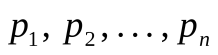 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 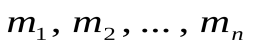 и молярными массами
и молярными массами 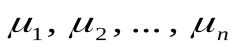 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,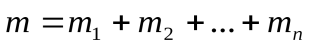 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
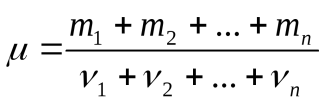 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (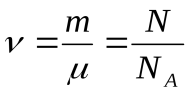 )
)
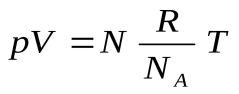 , (17.10)
, (17.10)
где 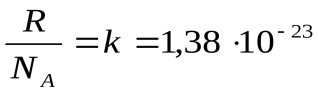
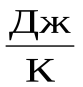 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 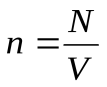 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П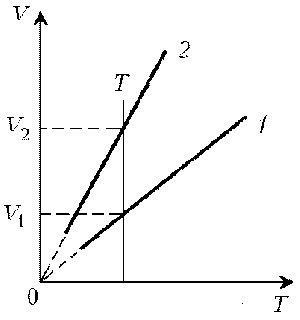 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П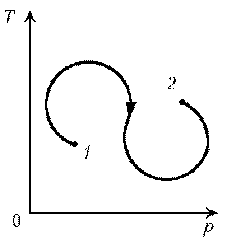 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П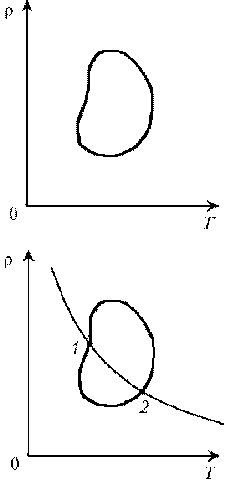 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
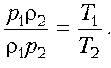
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
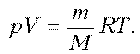
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
-
П ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
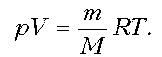
1–2: р = const; T = const; V
m; m; V.
2–3: р = const; m = const; V
T; T; V.
3–4: р = const; T = const; V
m; m; V
4–1: р = const; m = const; V
T; T; V.
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
-
П ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .
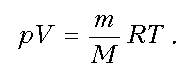
1–2: T = const, р = const; V
m; V; m
2–3: T = const, р
1/V; m = const; р
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 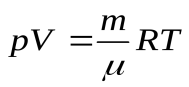 . (17.2)
. (17.2)
где R = 8,31 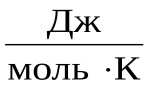 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
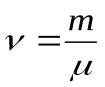 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 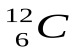 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 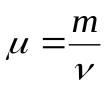
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
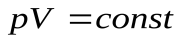 или
или 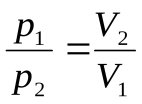 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
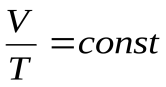 или
или 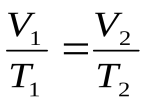 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
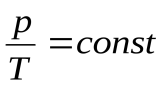 или
или 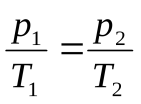 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 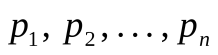 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 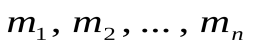 и молярными массами
и молярными массами 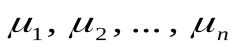 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,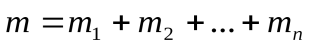 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
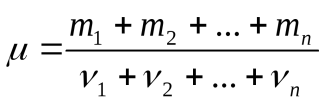 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (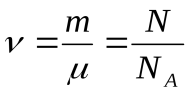 )
)
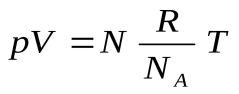 , (17.10)
, (17.10)
где 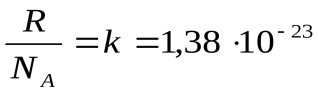
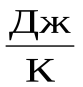 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 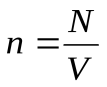 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П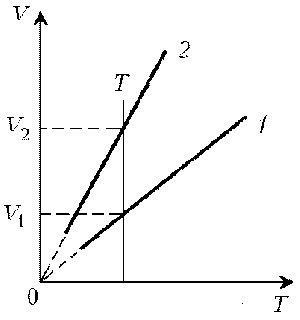 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П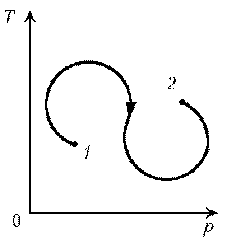 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П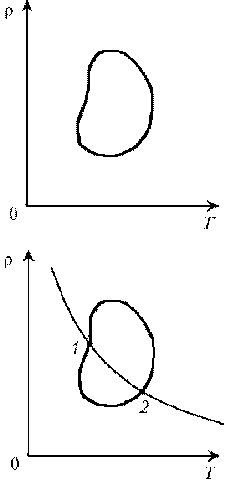 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
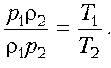
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
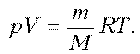
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
-
П ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
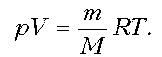
1–2: р = const; T = const; V
m; m; V.
2–3: р = const; m = const; V
T; T; V.
3–4: р = const; T = const; V
m; m; V
4–1: р = const; m = const; V
T; T; V.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 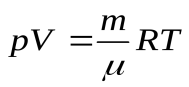 . (17.2)
. (17.2)
где R = 8,31 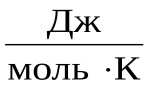 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
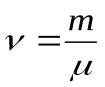 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 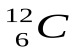 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 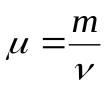
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
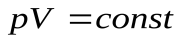 или
или 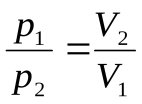 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
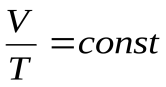 или
или 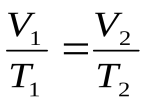 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
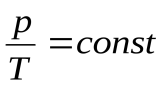 или
или 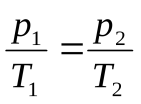 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 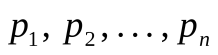 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 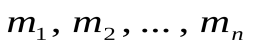 и молярными массами
и молярными массами 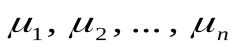 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,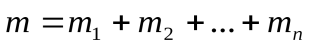 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
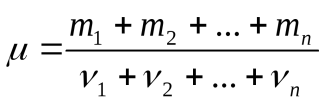 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (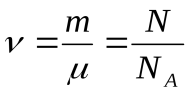 )
)
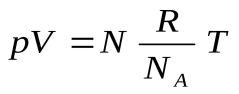 , (17.10)
, (17.10)
где 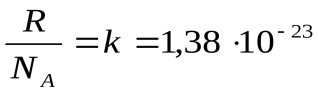
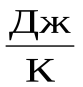 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 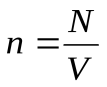 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П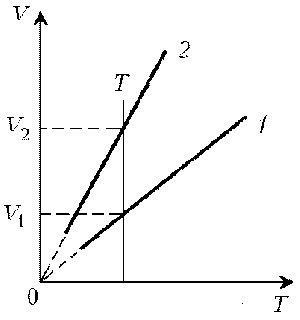 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П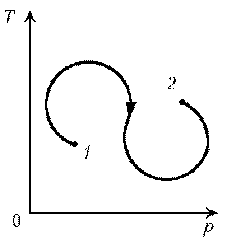 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П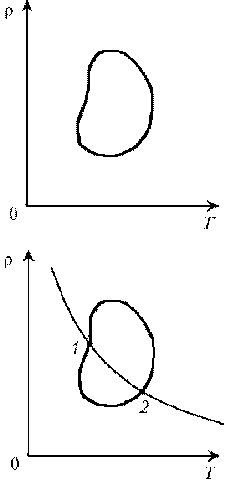 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
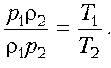
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
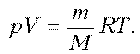
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
-
П ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
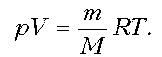
1–2: р = const; T = const; V
m; m; V.
2–3: р = const; m = const; V
T; T; V.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 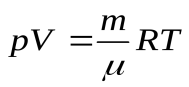 . (17.2)
. (17.2)
где R = 8,31 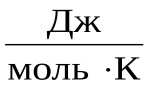 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
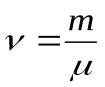 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 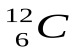 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 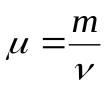
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
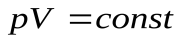 или
или 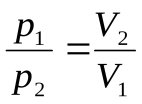 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
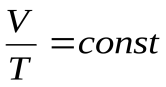 или
или 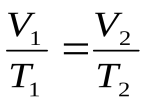 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
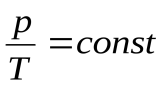 или
или 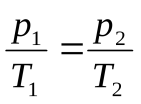 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 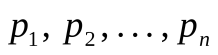 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 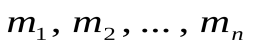 и молярными массами
и молярными массами 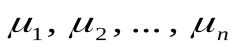 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,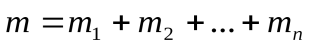 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
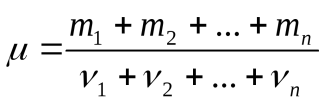 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (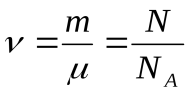 )
)
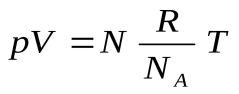 , (17.10)
, (17.10)
где 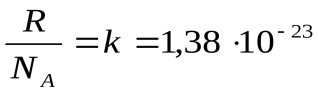
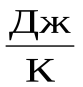 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 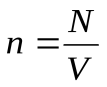 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П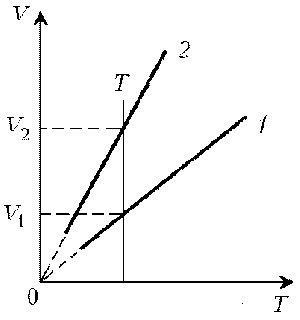 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П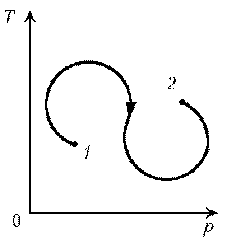 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П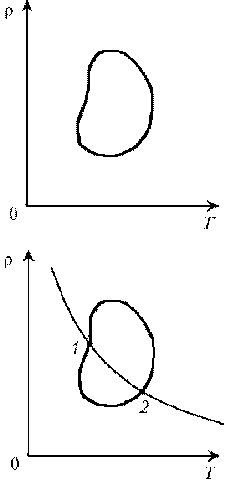 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
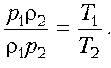
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
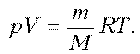
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
3–4: T = const, V = const; m
р; p; m
4–1: T = const, р = const; m
V; V; m
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 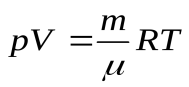 . (17.2)
. (17.2)
где R = 8,31 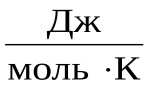 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
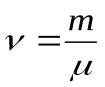 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 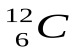 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 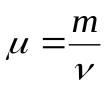
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
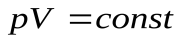 или
или 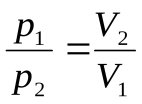 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
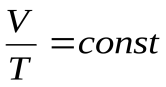 или
или 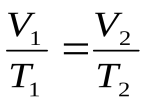 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
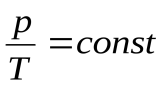 или
или 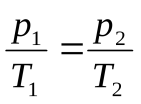 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 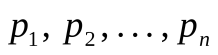 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 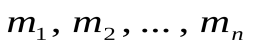 и молярными массами
и молярными массами 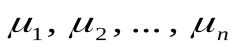 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,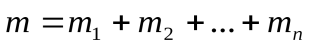 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
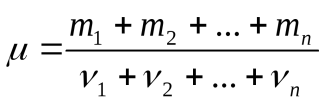 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (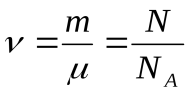 )
)
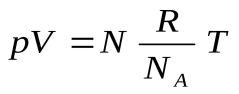 , (17.10)
, (17.10)
где 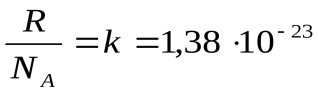
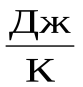 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 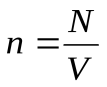 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П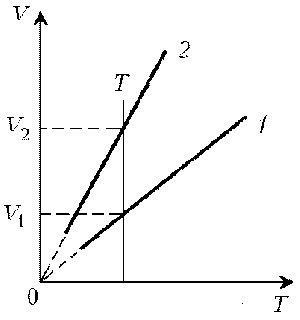 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П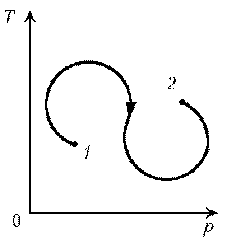 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П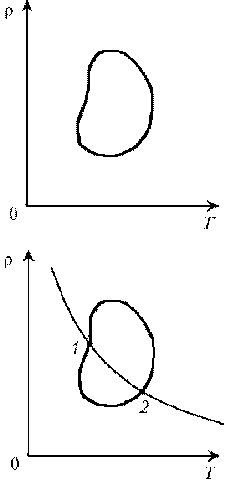 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
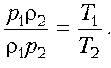
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
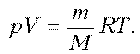
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
р; р; m
2–3: T = const, р = const; m
V; V; m
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 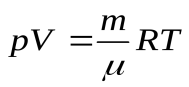 . (17.2)
. (17.2)
где R = 8,31 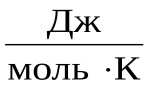 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
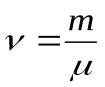 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 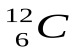 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 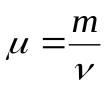
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
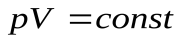 или
или 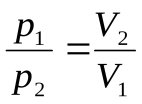 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
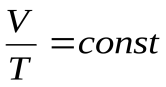 или
или 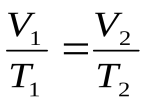 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
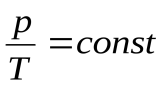 или
или 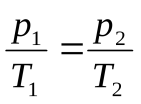 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 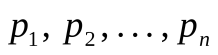 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 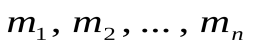 и молярными массами
и молярными массами 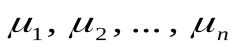 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,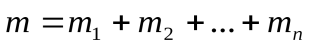 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
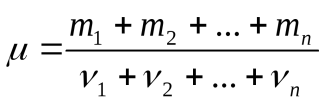 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (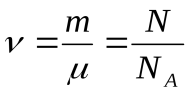 )
)
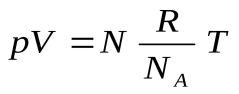 , (17.10)
, (17.10)
где 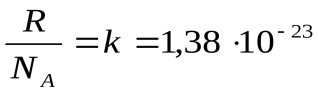
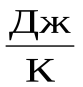 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 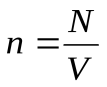 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П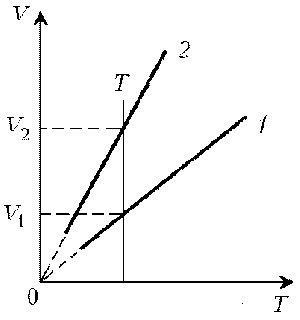 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П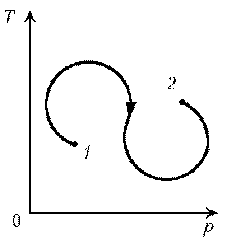 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П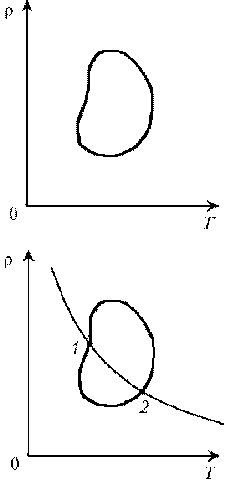 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
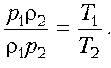
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется...
-
П ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
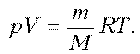
П о условию, T, M и R – постоянные, следовательно, m
о условию, T, M и R – постоянные, следовательно, m
рV.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 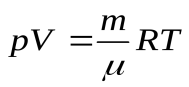 . (17.2)
. (17.2)
где R = 8,31 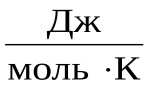 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
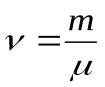 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 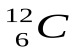 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 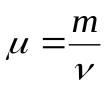
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
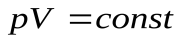 или
или 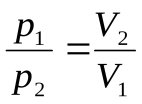 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
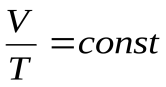 или
или 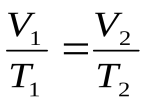 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
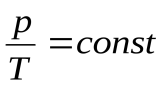 или
или 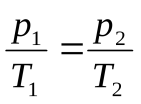 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 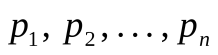 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 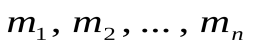 и молярными массами
и молярными массами 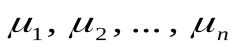 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,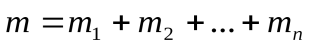 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
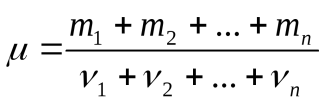 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (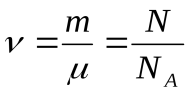 )
)
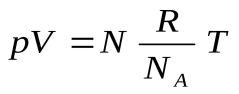 , (17.10)
, (17.10)
где 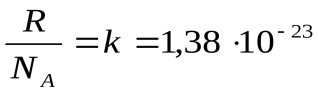
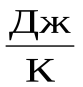 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 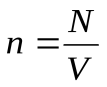 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П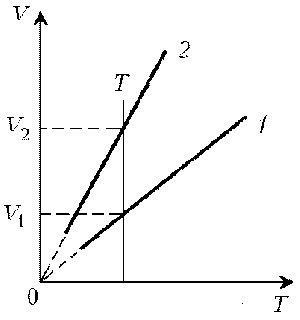 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
4–1: изохорический процесс; закон Шарля; р
T; р; T.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
-
П ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1 –1*: переход на более «высокую» изотерму, значит, температура растет.
–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
-
П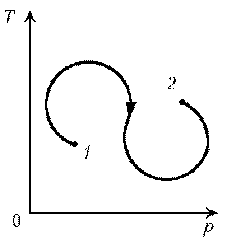 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При и зотермическом процессе р
зотермическом процессе р
1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 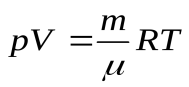 . (17.2)
. (17.2)
где R = 8,31 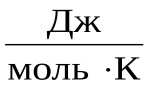 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
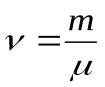 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 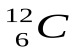 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 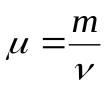
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
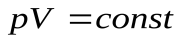 или
или 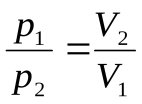 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
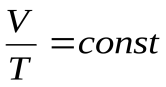 или
или 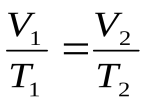 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
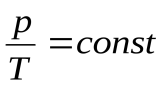 или
или 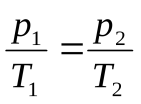 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 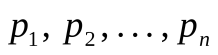 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 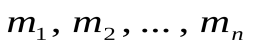 и молярными массами
и молярными массами 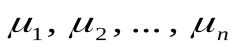 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,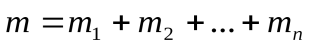 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
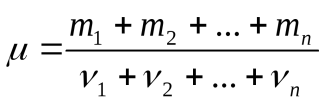 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (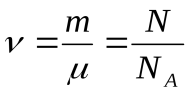 )
)
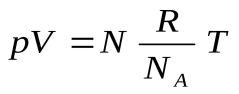 , (17.10)
, (17.10)
где 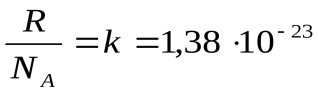
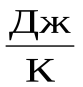 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 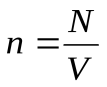 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П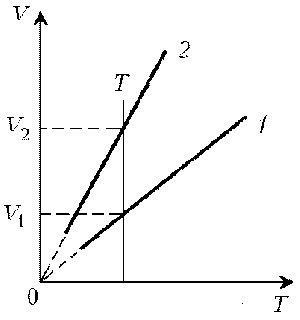 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
2 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V
T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 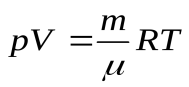 . (17.2)
. (17.2)
где R = 8,31 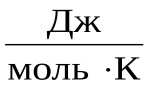 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
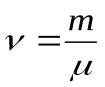 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 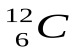 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 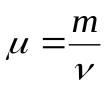
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
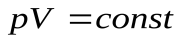 или
или 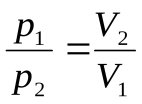 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
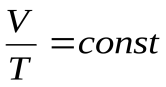 или
или 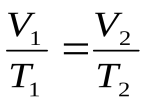 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
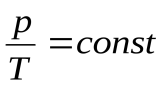 или
или 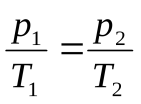 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где  – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами  и молярными массами
и молярными массами  можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,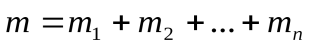 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
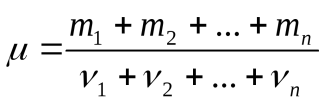 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (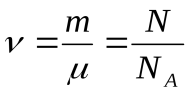 )
)
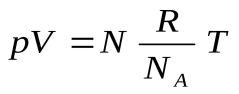 , (17.10)
, (17.10)
где 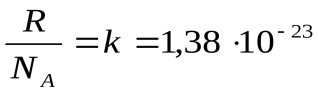
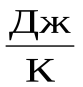 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 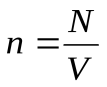 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П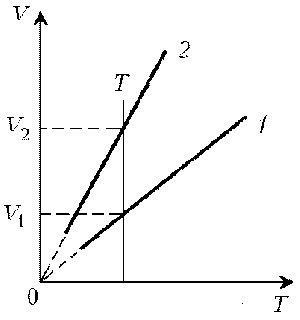 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
4–1: изохорический процесс; закон Шарля; р
T; р; T.
-
П ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 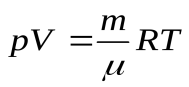 . (17.2)
. (17.2)
где R = 8,31 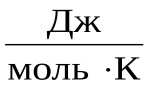 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
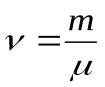 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 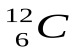 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 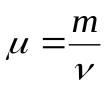
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
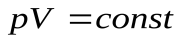 или
или 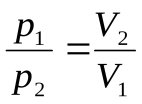 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
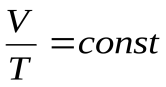 или
или 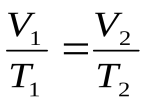 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
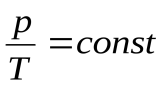 или
или 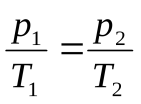 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 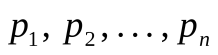 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 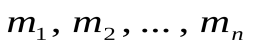 и молярными массами
и молярными массами 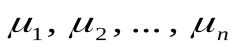 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,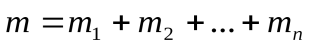 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
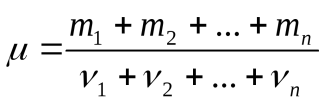 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (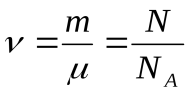 )
)
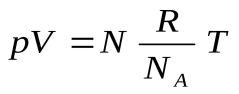 , (17.10)
, (17.10)
где 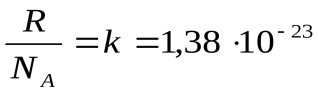
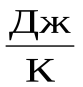 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 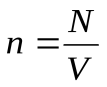 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П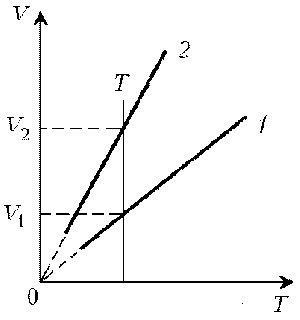 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
2–3: изохорический процесс; закон Шарля; р
T; р; T.
3–4: изобарический процесс; закон Гей-Люссака; V
T; V; T.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 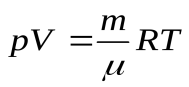 . (17.2)
. (17.2)
где R = 8,31 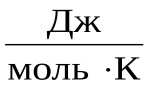 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
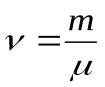 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 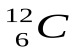 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 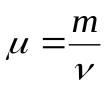
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
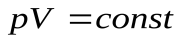 или
или 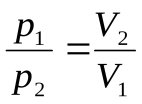 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
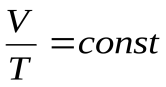 или
или 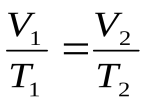 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
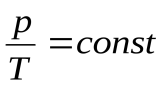 или
или 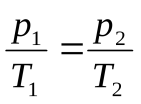 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где  – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами  и молярными массами
и молярными массами  можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,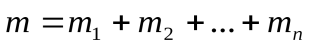 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
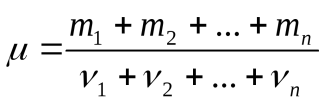 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (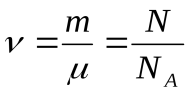 )
)
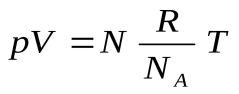 , (17.10)
, (17.10)
где 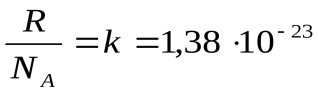
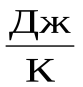 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 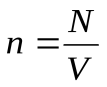 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П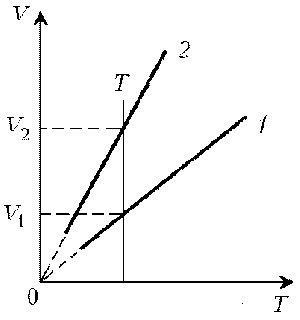 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
3–1: изобарический процесс; закон Гей-Люссака; V
T; T; V.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
-
П ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
1 –2: изобарический процесс; закон Гей-Люссака; V
–2: изобарический процесс; закон Гей-Люссака; V
T; V; T.
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 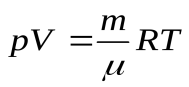 . (17.2)
. (17.2)
где R = 8,31 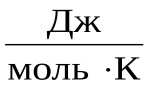 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
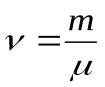 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 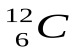 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 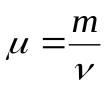
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
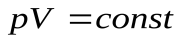 или
или 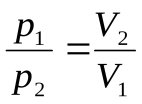 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
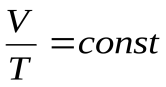 или
или 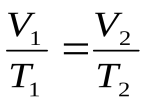 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
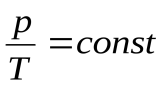 или
или 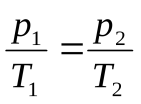 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где 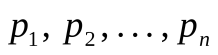 – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами 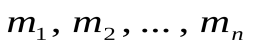 и молярными массами
и молярными массами 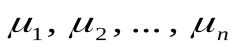 можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,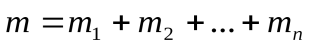 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
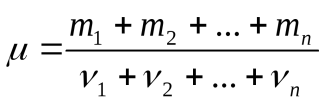 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (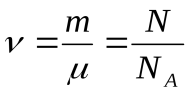 )
)
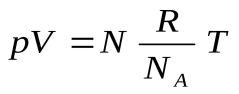 , (17.10)
, (17.10)
где 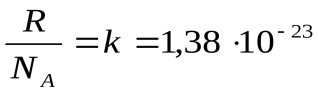
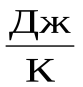 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 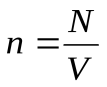 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П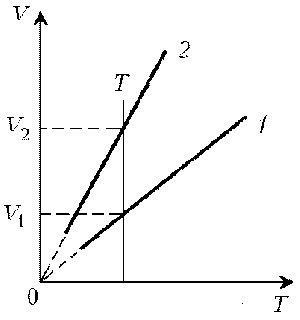 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р
T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р
1/V; р; V
Практическая работа № 6 и 7
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА и Изопроцессы на графике
Контрольные вопросы для подготовки к занятию – ответить на эти вопросы в письменном виде!
1. Какой газ называется идеальным?
2. Какие физические величины характеризуют идеальный газ? Дайте их определения и единицы измерения.
3. Что называется процессом, изопроцессом?
4. Сформулируйте и запишите уравнения изопроцессов. Начертите диаграммы в координатах рV, VT, рT.
5. Запишите уравнение состояния идеального газа для произвольной массы.
6. Запишите выражение и сформулируйте закон Дальтона.
!!! После изучения теоретической части и разбора приведенных и решенных (ниже по тексту) задач надо перейти в конец файла (стр. 23 и 25), где даны задания по 6-й и 7-й практическим работам для самостоятельного их выполнения
Краткие теоретические сведения и основные формулы
В молекулярно-кинетической теории пользуются моделью идеального газа, в котором:
- молекулы газа считаются материальными точками;
- столкновения молекул газа между собой и со стенками сосуда абсолютно упругие;
- потенциальной энергией взаимодействия между молекулами по сравнению с их кинетической энергией пренебрегают.
Модель идеального газа можно применять и при изучении реальных газов, так как многие газы (азот, водород, гелий, кислород, воздух и др.) в условиях, близких к нормальным, а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки на собственный объем (размеры) молекул и действующие молекулярные силы (потенциальную энергию), можно перейти к теории реальных газов.
Состояние заданной массы газа определяется значениями трех его параметров: давления р, объема V и термодинамической температуры Т. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически в виде функции
f (р, V, T) = 0. (17.1)
Соотношение (17.1), определяющее связь между параметрами, представляет собой уравнение состояния данной массы газа.
Уравнением состояния идеального газа является уравнение Менделеева – Клапейрона: 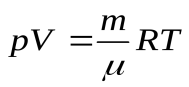 . (17.2)
. (17.2)
где R = 8,31 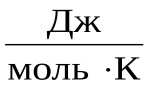 – молярная (универсальная) газовая постоянная.
– молярная (универсальная) газовая постоянная.
Отношение массы вещества к его молярной массе равно числу молей:
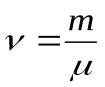 . (17.3)
. (17.3)
Моль – единица количества вещества, равная такому его количеству, в котором содержится столько же структурных элементов (атомов, молекул, ядер), сколько содержится атомов в 0,012 кг изотопа углерода 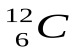 . Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
. Из определения моля следует, что 1 моль различных веществ (газообразных, жидких, твердых) содержит одинаковое число АвогадроNА = 6,022.1023 моль-1 структурных элементов.
Молярная масса – это масса одного моля вещества: 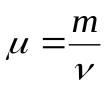
 (17.4)
(17.4)
Процессы, протекающие при каком-либо постоянном термодинамическом параметре, называются изопроцессами.
Процесс, протекающий при постоянной температуре называется изотермическим
Для данной массы (т = const) определенного ( = const) газа произведение  , и тогда уравнение (17.2) можно записать в виде
, и тогда уравнение (17.2) можно записать в виде
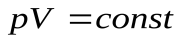 или
или 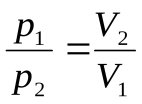 , (17.5)
, (17.5)
что является выражением опытного закона Бойля - Мариотта. Кривая, изображающая зависимость между давлением и объемом при Т = const, н азывается изотермой (рис.17.1).
азывается изотермой (рис.17.1).
Рис. 17.1
Процесс, происходящий при постоянном внешнем давлении, называется изобарным. Он подчиняется закону Гей-Люссака
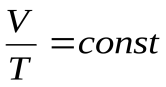 или
или 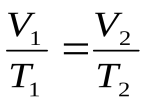 (17.6)
(17.6)
при m = const, = const.
На диаграмме в координатах V, T этот процесс изображается прямой, называемой изобарой (рис.17.2).
Р ис.17.2
ис.17.2
Процесс, происходящий при постоянном объеме, называется изохорным. Он подчиняется закону Шарля
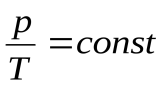 или
или 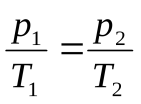 (17.7)
(17.7)
при m = const, = const.
На диаграмме в координатах р, Т он изображается прямой, н азываемой изохорой (рис.17.3)
азываемой изохорой (рис.17.3)
Рис.17.3
Для смеси идеальных газов справедлив закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений, входящих в нее газов, т.е.
 ,
,
где  – парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
– парциальные давления - давления, которые оказывали бы газы смеси, если бы они одни занимали объем, равный объему смеси при той же температуре.
И тогда уравнение состояния для смеси газов с массами  и молярными массами
и молярными массами  можно записать также в виде (17.2), где
можно записать также в виде (17.2), где ,
,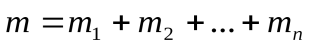 , а молярная масса смеси газов (согласно ее определению) равна
, а молярная масса смеси газов (согласно ее определению) равна
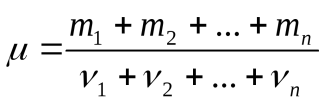 . (17.8)
. (17.8)
Согласно определению числа Авогадро, число молекул, содержащихся в молях, равно
N = NA . . (17.9)
И тогда уравнение (17.2) примет вид (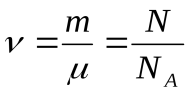 )
)
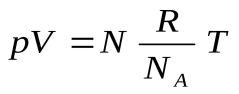 , (17.10)
, (17.10)
где 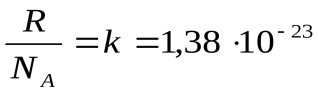
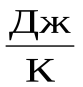 – постоянная Больцмана.
– постоянная Больцмана.
Поделив обе части равенства (17.9) на объем V, получим уравнение состояния идеального газа в виде
р = n k T, (17.11)
где 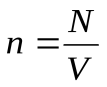 - концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
- концентрация частиц – число частиц в единице объема. Давление газа прямо пропорционально концентрации молекул и его температуре.
Уравнения (17.2) и (17.11) описывают равновесные состояния идеального газа.
Равновесным состоянием газа называется такое состояние, при котором все его параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Соотношение между температурой Т, измеренной по термодинамической шкале, и температурой t, измеренной по шкале Цельсия, следующее: Т = t + 273,15 К.
Главная страница «Первого сентября» • Главная страница журнала «Физика» • Содержание №29/2003
Архив
М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые законы
Г рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
рафические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
-
П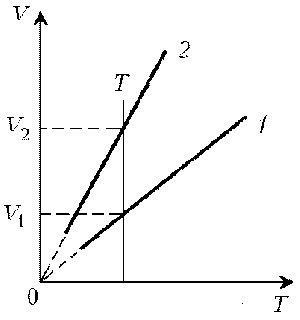 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за линии. Эти линии выражают прямо пропорциональную зависимость между объемом газа и его температурой, а это возможно для идеального газа только при изобарическом процессе, следовательно, изображенные линии графика – изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
-
П ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то, что линия графика не описывается ни одним из изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V
T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то 1 > 2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.П
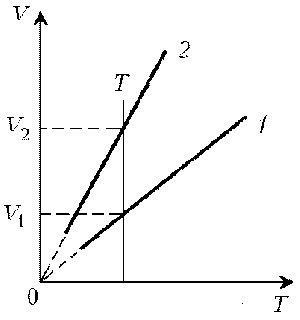 ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
ример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?П
 ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
ример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
-
П ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
ример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1
 –2: изохорический процесс; закон Шарля; р
–2: изохорический процесс; закон Шарля; р 3–1: изобарический процесс; закон Гей-Люссака; V
П
 ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.
ример 4. Для постоянной массы идеального газа представлен цикл на диаграмме р, V. Изобразить этот цикл на диаграмме V, T.2–3: изохорический процесс; закон Шарля; р
4–1: изохорический процесс; закон Шарля; р
П
 ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
ример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.2
 –3: изобарический процесс; закон Гей-Люссака; V
–3: изобарический процесс; закон Гей-Люссака; V4–1: изохорический процесс; закон Шарля; р
П
 ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
ример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.П
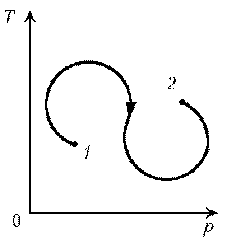 ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
ример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?1–А: р1 > рA V1 < VA 1 > А .
А–В: рВ > рА VВ < VА В > А
В–2: рВ > р2 VВ < V2 В > 2
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
-
П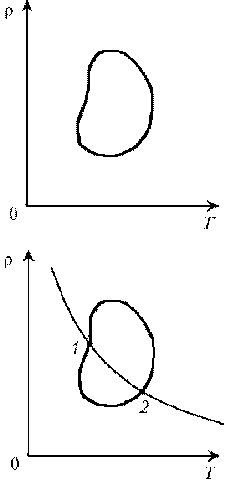 ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
ример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/. Тогда:
р1V1 = р1m/1 = RT1;
р2V2 = p2 m/2 = RT2.
Теперь остается разделить одно уравнение на другое:
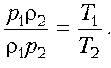
Но р1 = р2, значит, 1T1 = 2T2, или T = const, или
П
 ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
ример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m
3–4: T = const, V = const; m
-
П ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
ример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:

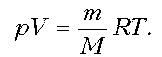
1–2: р = const; T = const; V
3–4: р = const; T = const; V
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
-
П ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
ример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .

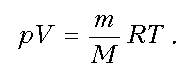
1–2: T = const, р = const; V
3–4: T = const, V = const; р
ЗАДАЧИ ПО ИЗОПРОЦЕССАМ
Изо- - значит, неизменный, равный. Изопроцесс - это такой процесс, который производят с газом либо при неизменной температуре, либо при неизменном давлении, либо при неизменном объеме. При этом газ подчиняется уравнению состояния идеального газа, которое превращается в каждом процессе либо в закон Бойля-Мариотта, либо в закон Гей-Люссака, либо в закон Шарля, в зависимости от того, какая величина сохраняет свое значение.
Примеры решения задач
Задача 1. График перехода газа из состояния 1 в состояние 2 в координатах р, Т изображен на рис. 17.4. Как изменился при этом объем газа, если масса газа не изменилась?
Р
 ешение
ешениеПроведем через точки 1 и 2 две изохоры (рис.17.4). Одна изохора соответствует объему V1, другая – V2. Из рис.17.4 видно, что углы наклона изохор
Тогда
а так как
то
Из уравнения Менделеева - Клапейрона найдем
т.е.
,
следовательно, из неравенства (1) получим
Ответ:
Задача 2. На рис.17.5 представлены две изобары для одной и той же массы газа. Найдите отношение давлений, если углы наклона изобар равны
Решение
Найдем для одной и той же температуры отношение
Из уравнения Менделеева - Клапейрона
Т
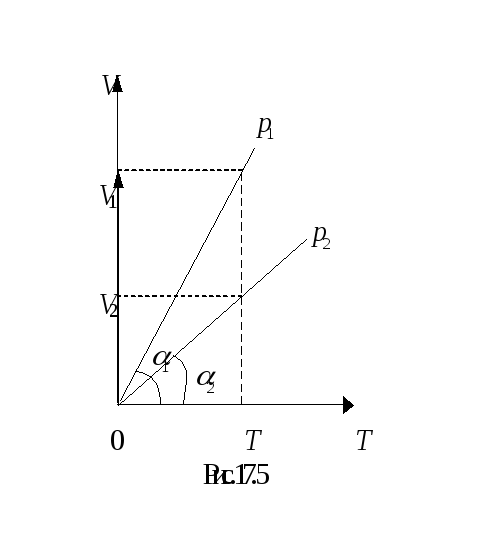 огда
огдаОтвет:
Задача 3. Идеальный газ находится в состоянии 1 с параметрами
Решение
Перевести газ из состояния 1 в состояние 2 можно с помощью изопроцессов.
I.
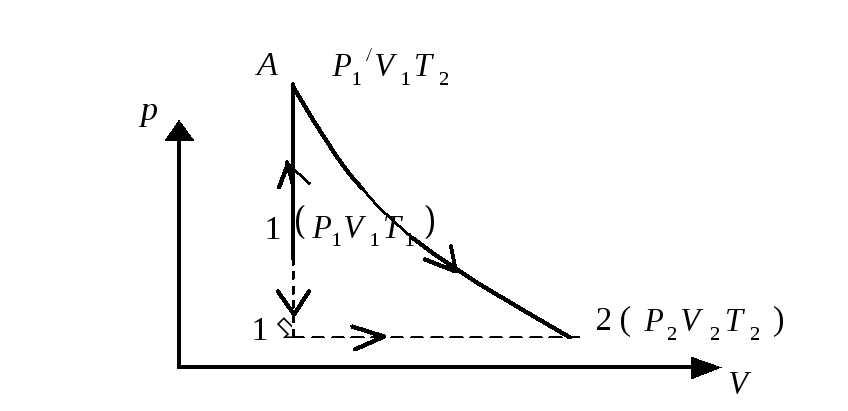 из состояния 1 в состояние 1 изохорно, т.е. V = const, а затем из 1 в 2 изобарно. В процессе 1-1
из состояния 1 в состояние 1 изохорно, т.е. V = const, а затем из 1 в 2 изобарно. В процессе 1-1 Рис. 17.6
II. Из 1-го во 2-е состояние можно перевести газ, если сначала газ нагреть при постоянном объеме до температуры Т2, а затем изотермически изменить его объем до V2 (расширить). При изотермическом процессе газ подчиняется закону Бойля - Мариотта рV = const при m = const, = const, T = const.
Задача 4. Замкнутый процесс (цикл) изображен в координатах р, V. Изобразите этот процесс в координатах р, T и V, T.
Решение
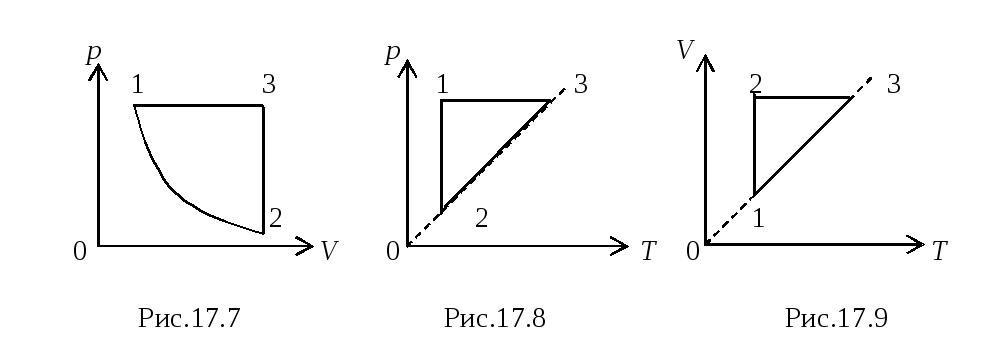
1. На участке 1-2 газ изотермически расширяется, его объем увеличивается, температура постоянна, давление падает. рV = const при m = const и = const. В координатах р, Т изотерма представляет собой прямую, параллельную оси давлений, причем давление падает (точка 1 выше точки 2) (рис.17.7).
2. На участке 2-3 газ изохорически нагревается, его давление увеличивается. В координатах р,Т изохора представляет собой прямую, проходящую через 0 и точку 2.
3. Участок 3-1 – изобара, причем температура на этой прямой изменяется от Т3 до первоначальной Т1, следовательно, изобара должна проходить через первую точку параллельно оси температур. Так можно найти точку 3 в координатах р,Т (рис. 17.8).
Координаты V, T (рис. 17.9).
1. Участок 1-2 – изотерма, причем объем возрастает, значит точка 1 ниже точки 2 (см. рис.17.9).
2. Участок 2-3 – изохорное нагревание – прямая параллельная оси температур.
3. Участок 3-1 – изобарное охлаждение, причем система возвращается к первому состоянию. Точку 3 находим как точку пересечения изохоры и изобары.
Задача 5. На диаграмме V – T изображены процессы перехода идеального газа постоянного количества из состояния 1 в состояние 3. Каким соотношением связаны конечное давление Р3 и начальное давление Р1?
Решение
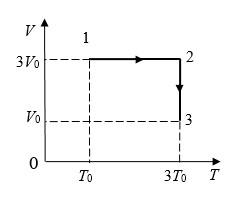
При изохорном процессе:
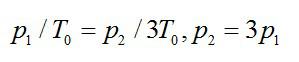
Далее при изотермическом:
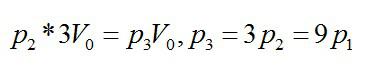
Ответ: Р3=9Р1
Задача 6. Для самостоятельного решения предлагается еще один цикл
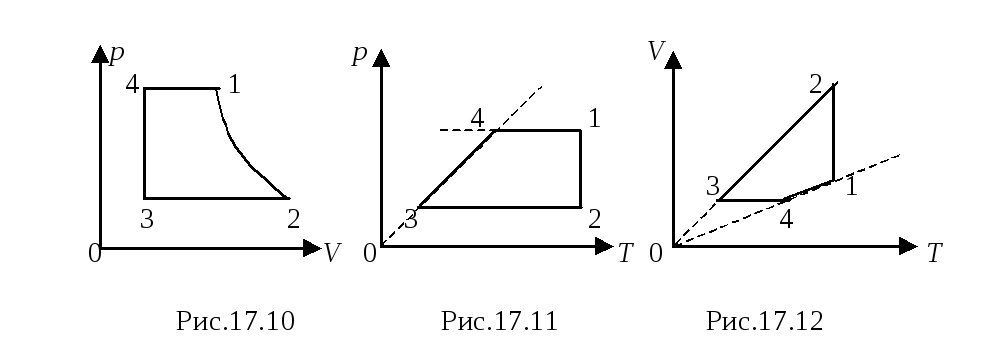
Примеры решения задач на графики изопроцессов - поэтапно
Задача 1. Перечертить процесс, происходящий с газом из осей
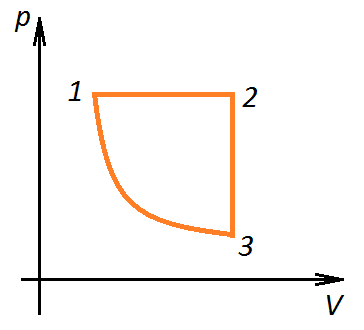
Начнем с анализа имеющегося графика. Итак, процесс 1-2 – изобара, потому что давление не меняется. Объем растет, следовательно, растет температура. Процесс 2-3 – изохора. Объем неизменен, давление падает – следовательно, и температура падает тоже. Последний участок – 3-1 – изотерма. Объем уменьшается, давление растет. Попробуем изобразить этот цикл в новых осях. Возьмем оси
Обратите внимание: начальную точку лучше ставить в центр, так как пока мы еще не знаем, куда нам предстоит затем двигаться: вверх, вниз, вправо или влево, и лучше будет оставить место для любого отрезка.
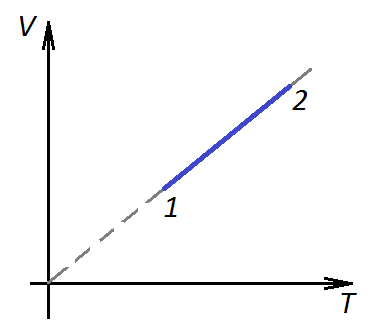
Следующий процесс – изохора – изображается в осях
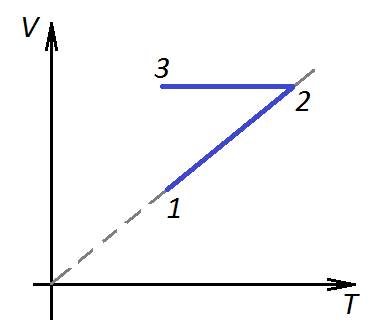
Ну и последний этап – изотерма, вертикальная прямая в осях
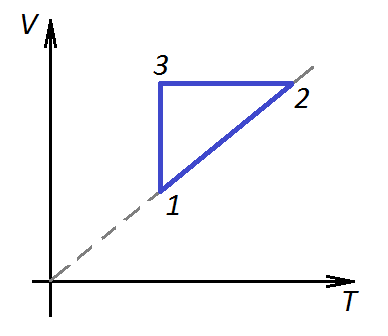
Теперь рассмотрим оси
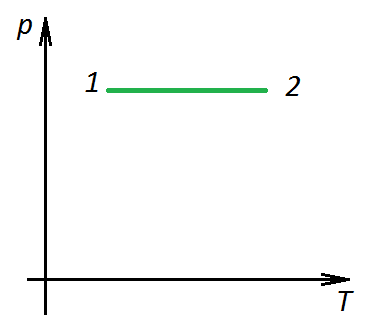
Следующий процесс – изохора – изображается в осях
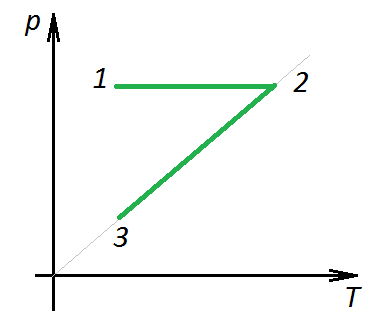
После чего по изотерме нужно подняться вверх до достижения начального давления
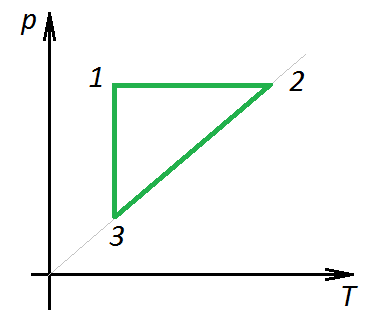
Задача 2. Перечертить процесс, происходящий с газом из осей
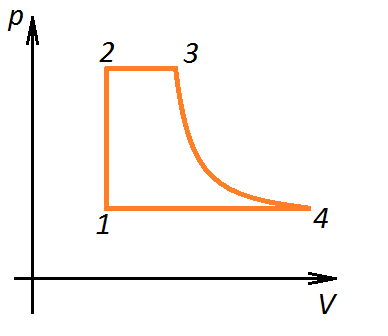
Проанализируем представленный цикл, можно даже подписать на нем названия процессов. Процесс 1-2 – изохора, давление растет, следовательно, и температура также. Затем следует изобара, объем растет, следовательно, температура тоже продолжает расти. Далее видим изотерму, по ней мы спускаемся до начального давления – давление падает, а значит, растет объем. Наконец, замыкает процесс опять изобара, но теперь объем уменьшается, следовательно, температура падает.