1. 
   Постановка задачи
   

Необходимопозаданнойструктурнойсхеменадежностиинформационнойсистемы и заданным значениям интенсивности отказов ее элементов, согласновыданномуварианту,необходимо:

1. 
   построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня не ниже 0,1;
   
2. 
   по графику вероятности безотказной работы определить время наработки системы, которое соответствует заданному гамма – процентному ресурсу системы;
   
3. 
   обеспечить за счет структурного резервирования элементов системы, при заданном увеличение времени наработки системы не менее чем в 1,5 раза.
   

2. 
   Ход работы
   

Нарисунке1представленаструктурнаясхеманадежнойсистемы.

---

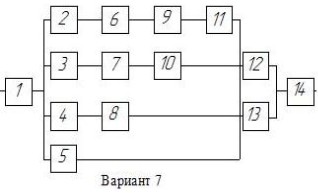
Рисунок 1 - Структурная схема надежной системыИсходныезначенияинтенсивностиотказовэлементовсоставляют:- ^{λ1=0.05x10−61/ч}- ^{λ2=λ3=λ4=0.5x10−61/ч}- ^{λ5=λ6=λ7=λ8=0.005x10−61/ч}- ^{λ9=λ10=1.0x10−61/ч}- ^{λ11=0.1x10−61/ч}- ^{λ12=λ13=0.2x10−61/ч}- ^{λ14=0.1x10−61/ч}- ^{γ= 65%}где– вероятность безотказной работы системы, по истечении определенноговременинепрерывнойработы(наработки)системы,выраженныйвпроцентах.Всеэлементысистемыработаютврежименормальнойэксплуатации.Резервированиеотдельныхэлементовили групп элементовдолжноосуществлятьсяидентичнымипонадежностирезервнымиэлементамиилигруппамиэлементов.Переключателиприрезервированиисчитаютсяидеальными.Насхемеобведенныепунктиромmэлемента

---

являютсяфункциональнонеобходимыми.Произведемрасчетвероятностибезотказнойработызаданнойсхемынадежности.Висходнойсхемеэлементы2,6,9и11образуютпоследовательноесоединение.ЗаменяемихквазиэлементомA.Расчитываемпоформуле:P_A=q₂q₆q₉q₁₁Элементы3,7и10образуютпоследовательноесоединение,котороезаменяемэлементом B.P_B=q₃q₇q₁₀Элементы 4 и 8 образуют последовательное соединение, которое заменяемэлементомС.P_С=q₄q₈В преобразованной схеме элементы A, B, C и 5 образуют параллельноесоединение.Рассчитываемпо формуле:P_D=1-П(1-qi)=1-[(1-qA)*(1-qB)*(1-qC)*(1-q5)]Висходнойсхемеэлементы12,13образуютпараллельноесоединение.ЗаменяемихквазиэлементомE.Учитывая,чтоp₈p₉p₁₀,получимP_E=1-[(1-q12)*(1-q13)]Преобразованнаясхемаизображенанарисунке2.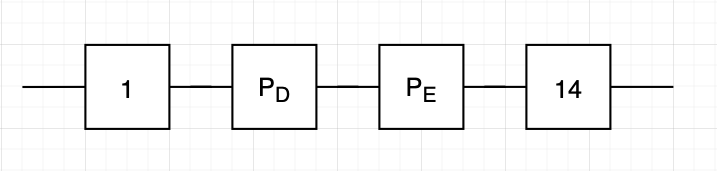Рисунок2–ПреобразованнаясхеманадежностиВпреобразованнойсхемеэлементы1,D,Eи14образуютпоследовательноесоединение.ТогдавероятностьбезотказнойработывсейсистемыопределяетсявыражениемP=p₁p_Dp_Ep₁₄.Таккакпоусловиювсеэлементысистемыработаютвпериоденормальнойэксплуатации,товероятностьбезотказнойработыэлементовс1по14подчиняютсяэкспоненциальномузаконуp

---

_i(t)=e^−λit.Результатырасчетоввероятностейбезотказнойработыэлементов1-14исход-нойсхемыпоприведеннойвышеформуледлянаработкидо3 0,03*106 часовпредставленыв таблице1.Таблица1–Результатырасчетоввероятностейбезотказнойработы

	Наработка, t – 30000ч
Элемент	λ, 10−6	0,5	1	1,5	2	2,5	3
1	0,05	0,9993	0,9985	0,9978	0,9970	0,9963	0,9955
2,3,4	0,5	0,9925	0,9851	0,9778	0,9704	0,9632	0,9560
5,6,7,8	0,05	0,9993	0,9985	0,9978	0,9970	0,9963	0,9955
9,10	0,005	0,9999	0,9999	0,9998	0,9997	0,9996	0,9996
11	0,1	0,9985	0,9970	0,9955	0,9940	0,9925	0,9910
12,13	0,2	0,9970	0,9940	0,9910	0,9881	0,9851	0,9822
14	0,1	0,9970	0,9970	0,9971	0,9971	0,9971	0,9971
A	-	0,9902	0,9805	0,9710	0,9615	0,9521	0,9428
B	-	0,9917	0,9835	0,9753	0,9672	0,9592	0,9513
C	-	0,9918	0,9836	0,9756	0,9675	0,9596	0,9517
D	-	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000
E		0,9940	0,9881	0,9822	0,9763	0,9704	0,9646
P	-	0,9903	0,9837	0,9771	0,9705	0,9640	0,9576

---

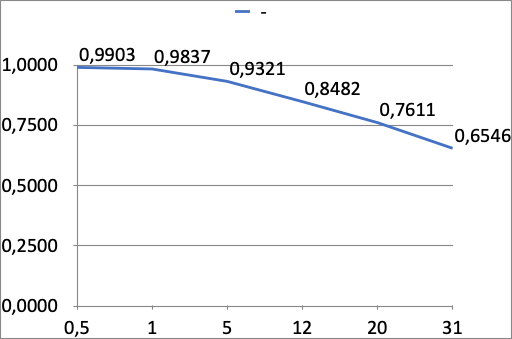
Результаты расчетов вероятностей безотказной работы квазиэлементов A,B,С, D, EиPтакжепредставлены втаблице1.Пополученнымрезультатамстроимграфикзависимостивероятностибезотказной работы системы от времени эксплуатации, представленный нарисунке3.Рисунок3–Графикзависимостивероятностибезотказнойработысистемыотвремениэксплуатацииусловиям задания находим время, превышающее в 1,5 раза время,соответствующеевероятности безотказнойработы, равное0,65(P_γ=0,65).t′=1,5*t=1,395*10⁶ч

---

Смотрите также файлы

• Лабораторная работа Базовые логические операции и, или, не.docx

• Отчет по лабораторной работе 3 По дисциплине Химия (наименование учебной дисциплины, согласно учебному плану).docx

• Московская международная академия.docx

• Износостойкие сопла для распыления абразивных суспензий.pdf

• Туляремия.docx