Лабораторная работа 1.

Базовые логические операции: и, или, не

Теоретическое введение:

Цель работы: изучение принципа работы базовых логических элементов и устройств, реализующих основные логические операции.

Основными операциями булевой алгебры являются отрицание (инверсия), логическое сложение (дизъюнкция) и логическое умножение (коньюнкция).

Логической переменной можно называть высказывание, относительно которого, можно однозначно сказать истинно оно или ложно. При этом третьего варианта не дано. Таблица истинности логической переменной представляет собой таблицу, в которой записаны все возможные варианты состояния этой переменной.

Рассмотрим основные логические операции.

Отрицание – такая логическая операция над одной переменной, в результате которой появляется новое высказывание, которое принимает истинное значение, если входное высказывание истинно. Отрицание обозначается чертой над переменной, например, Ā читается «НЕ А». Таблица истинности этой операции приведена на рисунке 1а.

Инвертор (НЕ) логическое отрицание

Таблица истинности И Обозначение

X	__ X,  X
0	1
1	0

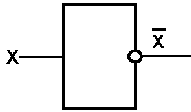
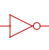
Рис. 1а

Логическое сложение – такая логическая операция над двумя и более исходными данными (высказываниями), в результате которой появляется новое сложное высказывание, принимающее истинное значение, если истинно хотя бы одно из высказываний, и ложное, если одновременно ложны все исходные высказывания. Обозначается знаком плюс, например, А+В читается «А ИЛИ В». Таблица истинности операции логического сложения над двумя переменными приведена на рисунке 1б.

Дизъюнкция (И) логическое сложение

Таблица истинности И Обозначение

X	Y	X+Y
0	0	0
0	1	1
1	0	1
1	1	1

---

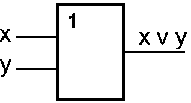
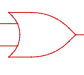
Рис. 1б

Логическое умножение – такая логическая операция над двумя и более исходными данными (высказываниями), в результате которой появляется новое сложное высказывание, принимающее истинное значение, если одновременно истинны все исходные высказывания, и ложное, если ложно хотя бы одно из исходных высказываний. Обозначается в виде произведения в обычной алгебре, например, А˟В, А·В.

Таблица истинности операции логического умножения над двумя переменными приведена на рисунке 1в.

Конъюнкция (И) логическое умножение

Таблица истинности И Обозначение (наше) (зарубежное)

X	Y	X*Y
0	0	0
0	1	0
1	0	0
1	1	1

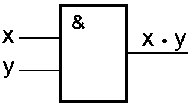
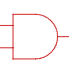
Рис. 1в

Логические функции – это выражения, состоящие из логических переменных (то есть переменных, способных принимать лишь два значения – 0 и 1) и операций над ними. Область науки, изучающая логические функции называется булевой алгеброй. Для описания логических функций существует несколько способов: математическое выражение и таблица истинности. Таблица истинности логической функции представляет собой таблицу, в которой записаны все возможные варианты состояния системы (значения переменных) и соответствующие им значения логической функции.

Используя основные логические операции, можно реализовать логическую схему (структуру) любой степени сложности, выполняющую заданный закон функционирования, т.е. основные логические операции образуют функционально полный набор логических элементов.

Задача синтеза сложных логических схем эквивалентна представлению

---

сложных булевых функций простыми функциями, в качестве которых могут быть использованы операции И, ИЛИ, НЕ, образующие функционально полный набор логических элементов, то есть позволяют реализовать логическую схему любой сложности. На самом деле существует ряд других логических операций (импликация, эквивалентность, штрих Шеффера, стрелка Пирса), но все их можно выразить через базисные.

Данные логические элементы, даже можно комбинировать попарно (ИЛИ, НЕ) и (И, НЕ) и вместе они составляют полный логический базис (рисунок 2)

Схема И-НЕ

Таблица истинности И-НЕ Обозначение

X	Y	____ X*Y
0	0	0
0	1	1
1	0	1
1	1	1

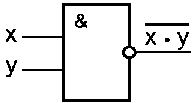
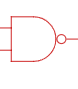
Схема ИЛИ-НЕ

Таблица истинности ИЛИ-НЕ Обозначение

X	Y	____ X+Y
0	0	0
0	1	1
1	0	1
1	1	1

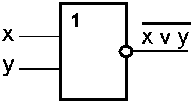
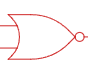
Рис. 2 Базисные функции

Каждая из функция И-НЕ, ИЛИ-НЕ является полным логическим базисом.

Экспериментальная часть

Работа в Nandgame

Целью экспериментальной части является изучение функционально полных наборов логических элементов и приобретение практических навыков реализации основных тождеств булевой алгебры на основе заданных функционально полных наборов логических элементов.

---

Порядок выполнения:

• 
  Зайти на сайт nandgame.com.
  
• 
  При желании переключить интерфейс на русский.
  

• 
  Изучить интерфейс. Входы (input) в виде логических переменных, расположены снизу. Щелчком мыши по ним вы можете менять их состояние с 0 на 1 и обратно. Кроме них внизу находится блок питания (Power), он всегда выдает логическую единицу.
  
• 
  Ознакомиться с заданием, которое представлено в текстовом виде.
  
• 
  Изучить спецификацию, представленную в виде таблицы истинности логической функции.
  

• 
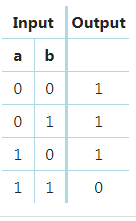
  Используя указанный в задании на лабораторную работу набор логических элементов, нарисовать схемы, реализующие логические операции для заданной логической функции.
  
• 
  Реализовать функцию управления, согласно спецификации. Для реализации вам представлены два электромеханических реле – нормально-разомкнутое (default off) и нормально – замкнутое (default on).
  

• 
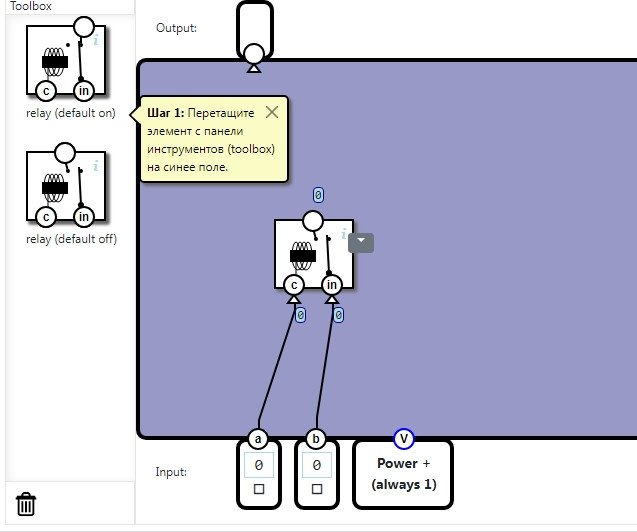
  Проверить своё решение, нажав кнопку «Check solution», при возникновении ошибок – исправить их.
  

• 
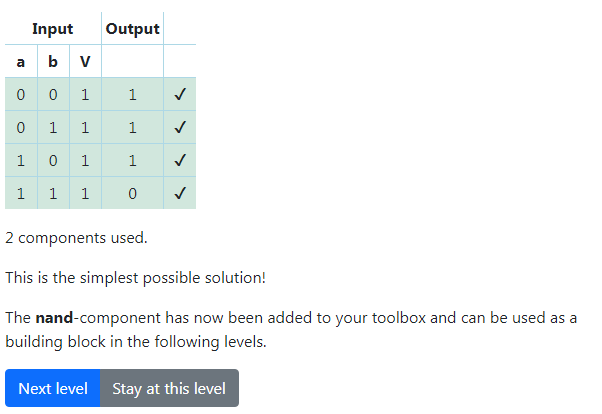
  Если уровень успешно пройден – перейти к следующему заданию, нажав на кнопку «Next level».
  
• 
  Повторить все пункты для следующей логической функции. Необходимо выполнить все задания уровня «Logic gates».
  

Работа в Tinkercad

• 
  Зарегистрироваться tinkercad.com (можно зарегистрировать отдельный аккаунт, можно зайти через Google account)
  
• 
  Зайти - Мои проекты – Цепи – Создать проект (выбрать Цепь)
  
• 
  Пустой проект - Основные элементы справа (лучше выбрать все)
  
• 
  Логика элементы И, Или, Не и т.д. и их описание.
  
• 
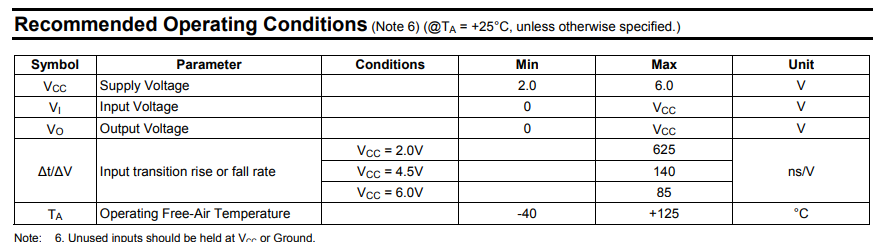
  Например схема 4 логических элемента И (74HC08), имеет питание, землю, 8 входов и 4 выхода, нужен Datasheet например https://www.diodes.com/assets/Datasheets/74HC08.pdf
  

---

• 
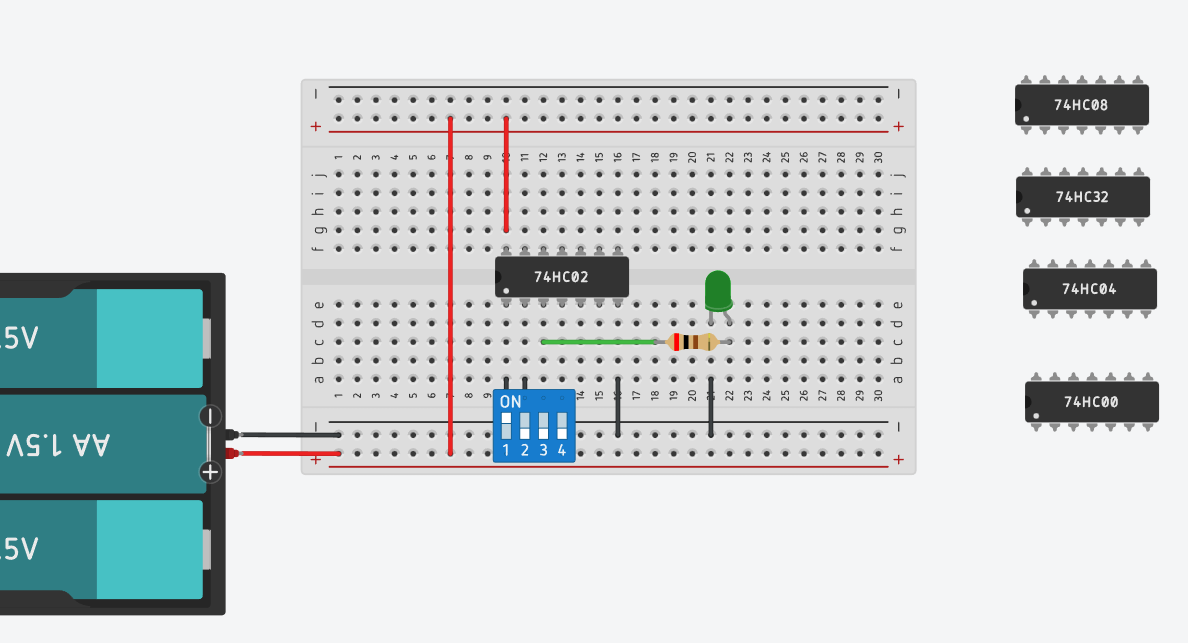
  Нужно питание Vcc например 4,5 или 6 В, (3-4 батареи по 1.5 В), переключатель для входов 1А, 1В (4 однополюсных DIP переключателя). Для идентификации значения на выходе можно использовать светодиод LED (как правило ток 20мA), а на выходе напряжение Vcc, поэтому нужен также резистор (100-200 Ом). Для удобства можно использовать малую макетную плату.
  
• 
  Создать схему для проверки и проверить таблицу истинности элементов (И. ИЛИ , НЕ, ИЛИ-НЕ, И-НЕ)
  
• 
  Ознакомиться с цепью в режиме принципиальной схемы и списка элементов.
  

Пример реализации Tinkercad -

• 
  Доказать что И-НЕ ИЛИ-НЕ являются полным логическим базисом. Т.е. реализовать с их помощью схемы И, ИЛИ, НЕ
  

Список контрольных вопросов

1. Что такое логическая операция?

2. Какие операции и тождества булевой алгебры Вы знаете?

3. Что такое логические операции? Логическое отрицание.

4. Логическое сложение. Логическое умножение.

5. Что такое таблица истинности?

6. Докажите основные тождества булевой алгебры.

7. Что такое булевы функции двух аргументов? Приведите примеры булевых функций.

8. Что такое функционально полный набор логических элементов? Приведите примеры функционально полных наборов.

9. Реализуйте булевы функции двух аргументов, используя функционально полные логические наборы:

а) И-НЕ; б) ИЛИ-НЕ; в) И, НЕ; г) ИЛИ, НЕ.

10. По заданной таблице определите логическую операцию.

Лабораторная работа 2. Синтез логических схем

Теоретическое введение:

Цель работы:

Ознакомиться с основными тождествами и законами булевой алгебры.

Основные тождества булевой алгебры

Комбинируя основные логические операции, можно получать новые, более сложные высказывания или суждения. Существует 15 основных тождеств булевой алгебры (тавтология), получающихся с помощью основных логических операций:

1 A+Ā=1 Элементарное высказывание

2 A·Ā=0 Элементарное высказывание

3 A+1=1 Элементарное высказывание

4 A·1=A Элементарное высказывание

5 A+A=A Соотношение абсорбции

6 A·A=A Соотношение абсорбции

7  A=А Двойное отрицание

8 (A+B)+C=A+(B+C) Сочетательное тождество для логической суммы

9 (AB)C=A(BC) Сочетательное тождество для логического произведения

10 A+B=B+A Переместительное тождество для логической суммы

---

Смотрите также файлы

• Отчет по лабораторной работе 3 По дисциплине Химия (наименование учебной дисциплины, согласно учебному плану).docx

• Московская международная академия.docx

• Износостойкие сопла для распыления абразивных суспензий.pdf

• Туляремия.docx

• Лицо привлечено к уголовной ответственности за незаконную предпринимательскую деятельность при сдаче в аренду жилого помещения третьим лицам без регистрации в качестве индивидуального предпринимателя.docx