Файл: Контрольная работа 1 вариант 1 по дисциплине Теория инженерного эксперимента л.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
ФГБОУ ВО «Кубанский государственный технологический университет»
ИНГЭ
КОНТРОЛЬНАЯ РАБОТА № 1 вариант №1
по дисциплине Теория инженерного эксперимента л
студент 1 курса, шифр 19-ОЗНМ-340 , специальность 21.04.01
Фамилия Ланцов д
Имя Александр Отчество Геннадьевич д
Дата поступления работы___________________________________
Оценка___________________Рецензент_____Шостак Н. А.______
« » 201 г. Подпись_____________
2019 г.
Объект исследованияв данной работе является передвижная парогенерирующая установка, производящая тепло в количестве Q, Дж, затрачивая дизельное топливо в количестве М, кг/с.
Задача данной работы: оптимизации работы- отношение Q/М должно быть максимальным, насколько это возможно.
Чаще всего в инженерной практике стремятся сформировать функцию типа y = f(x1,x2,...,xn), с помощью которой можно прогнозировать поведение объекта при изменении его параметров и условий работы, а также определять значения x1,x2,..., xn, соответствующие экстремальным значениям y.
Для нашего примера выберем три фактора: x1 – давление пара (атм), x2 – его расход (кг/с), x3 – площадь поверхности теплообмена (м2).
Таблица 1 – Кодирование факторов
| | X1 | X2 | X3 |
| Основной уровень 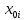 | 40 | 3 | 15 |
| Интервал варьирования 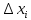 | 10 | 2 | 5 |
| Верхний уровень | 50 | 5 | 20 |
| Нижний уровень | 30 | 1 | 10 |
В данной работе воспользуемся методом полного факторного эксперимента для 3х факторов. Матрица планирования и результаты эксперимента приведены ниже в таблице 2.
С помощью ПФЭ ищут математическое описание процесса в виде уравнения:
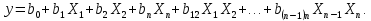
Его называют уравнением регрессии, а коэффициенты – коэффициентами регрессии.
Таблица 2 – Матрица планирования и результаты эксперимента
| № опыта | X0 | X1 | X2 | X3 | X1X2 | X1X3 | X2X3 | X1X2X3 | yэ (МДж/м3) | yрасч |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 31,4 | 31,3 |
| 2 | 1 | -1 | 1 | 1 | -1 | -1 | 1 | -1 | 31,3 | 31,2 |
| 3 | 1 | 1 | -1 | 1 | -1 | 1 | -1 | -1 | 31,9 | 31,8 |
| 4 | 1 | -1 | -1 | 1 | 1 | -1 | -1 | 1 | 31 | 30,8 |
| 5 | 1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 33 | 32,9 |
| 6 | 1 | -1 | 1 | -1 | -1 | 1 | -1 | 1 | 29,1 | 28,9 |
| 7 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 1 | 32 | 31,8 |
| 8 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 31,7 | 31,6 |
Рассчитаем линейные коэффициенты регрессии:
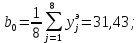
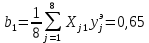
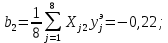
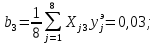
Теперь рассчитаем коэффициенты парного взаимодействия:
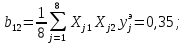
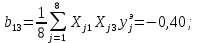
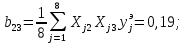
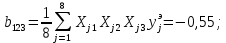
Некоторые из коэффициентов регрессии могут оказаться пренебрежимо малыми – незначительными. Для определения факта незначимости коэффициента необходимо определить оценки дисперсии, с которой они определялись. Для определения
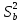вычислим: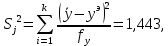
где k – число параллельных опытов (k = 3);
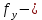число степеней свободы (
;
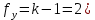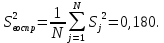
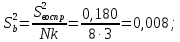
С оценками дисперсий
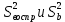связывают число степеней свободы: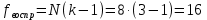
Принято считать, что коэффициент регрессии значим, если выполнено условие:
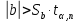
В таблице коэффициентов Стьюдента находим
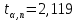для 
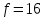и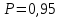 
. Тогда: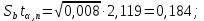
Для проверки значимости коэффициентов регрессии рассмотрим следующие соотношения:
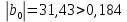
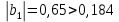
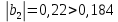
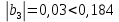
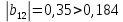
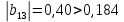
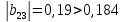
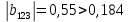
Видим, что коэффициент регрессии
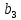незначим.Теперь проверим адекватность полученного уравнения регрессии. Эту проверку осуществляют с помощью критерия Фишера. Для начала вычислим оценку дисперсии адекватности:
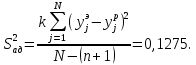
Число степеней свободы, связанных с этой оценкой дисперсии:
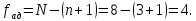
Расчетное значение критерия Фишера:
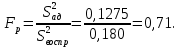
Табличное значение критерия Фишера
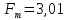. Условие 
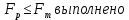. Следовательно, уравнение регрессииадекватно представленным результатам эксперимента: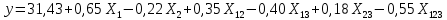
Перейдем в уравнении регрессии от кодированных переменных к физическим. Для этого представим кодированные переменные, используя таблицу 1, следующим образом:
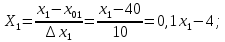
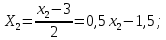
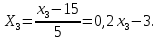
Подставим их в полученное выше уравнение регрессии и преобразуем:
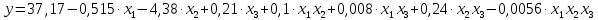
Используя полученное выше уравнение, исследователь избавляется от необходимости переводить всякий раз условия опыта в кодированные переменные.