Добавлен: 22.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт машиностроения
(наименование института полностью)
Кафедра "Сварка, обработка материалов давлением и родственные процессы"
(наименование кафедры/департамента/центра полностью)
15.03.01 Машиностроение
(код и наименование направления подготовки, специальности)
Технологии сварочного производства и инженерия поверхностей
(направленность (профиль) / специализация)
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №5
по учебному курсу «Высшая математика 2»
Вариант 1
| Студент | Перлухин А. В. (И.О. Фамилия) |
| Группа | пидб-2105а |
| Преподаватель | Лисненко А. П. (И.О. Фамилия) |
Тольятти 2023
| № п/п | Задача | Ответ |
| 1 | Вычислить объем тела, заданного представленными уравнениями, используя его поперечные сечения: | |
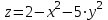 , , 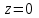 |  куб.ед. куб.ед. | |
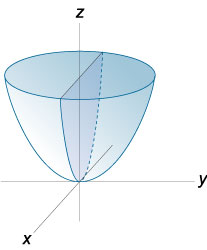 | ||
| Решение: Заданная фигура – эллиптический параболоид, отсекаемый плоскостью z = 0. Каноническое уравнение параболоида: 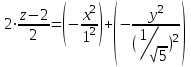 Уравнение сечения: 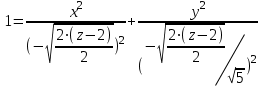 Это эллипс, площадь которого равна произведению полуосей: 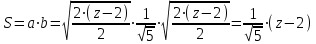 А объем тела, заданного уравнениями, и поперечным сечением равен: 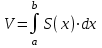 или или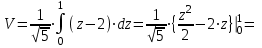 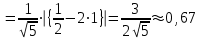 куб.ед. куб.ед. | ||
| 2 | Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, заданной представленными линиями: | |
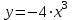 , , 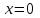 , , 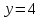 | 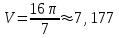 куб.ед. куб.ед. | |
| Чертеж: 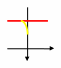 | ||
| Решение: Объем тела, образованного вращением вокруг оси ОХ определяется из формулы (тело заштриховано на рисунке): 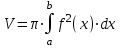 Линиями х = 0 и у = 4 определяются пределы интегрирования: х меняется в пределах от -1 до 0. А уравнение линии: у = -4х3. Тогда получаем: 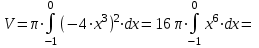 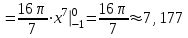 куб.ед. куб.ед. | ||