Файл: Контрольная работа по эконометрике контрольная работа выполняется на листах формата на титульном листе указываются.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 57
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 14.
х - среднемесячная оплата труда (ден. ед.);
у - уровень рентабельности торговой деятельности (у.е.).
| x | 127 | 133 | 149 | 156 | 162 | 182 | 197 | 201 | 195 | 204 |
| y | 2,01 | 2,12 | 2,77 | 3,62 | 3,80 | 4,01 | 4,33 | 4,54 | 4,20 | 4,60 |
Вариант 15.
х - среднемесячный товарооборот (на душу населения) (тыс. руб.);
у - уровень рентабельности (у.е.).
| x | 21 | 22 | 27 | 28 | 29 | 33 | 35 | 38 | 39 | 40 |
| y | 2,01 | 2,12 | 3,62 | 2,77 | 3,80 | 4,01 | 4,33 | 4,6 | 4,5 | 4,4 |
Вариант 16.
х - удельный вес продовольственных товаров в товарообороте (%);
у - уровень рентабельности (у.е.).
| x | 67 | 70 | 73 | 74 | 77 | 83 | 84 | 85 | 88 | 90 |
| y | 4,33 | 4,01 | 3,80 | 3,62 | 2,77 | 2,01 | 2,12 | 2,0 | 1,9 | 1,8 |
Вариант 17.
х - средняя заработная плата (тыс. руб.);
у - прожиточный минимум на душу населения (тыс. руб.).
| x | 41,08 | 31,63 | 30,04 | 26,49 | 30,97 | 28,90 | 32,77 | 28,69 | 40,57 | 30,62 |
| y | 14,9 | 12,9 | 14,6 | 15,2 | 13, 1 | 13,3 | 13,7 | 13,4 | 16,3 | 12,8 |
Вариант 18.
х - средняя взвешенная цена акций (руб.);
у - объем продаж (тыс. шт.).
| x | 84,4 | 82,4 | 80,1 | 63,4 | 76,2 | 75,1 | 74,8 | 73,0 |
| y | 79,5 | 279 | 71,4 | 243 | 76,3 | 74,7 | 211 | 75 |
Вариант 19.
x - объем выпуска продукции (тыс. ед.);
y - издержки производства (тыс. руб.).
| x | 1 | 2 | 4 | 3 | 5 | 3 | 4 | 6 |
| y | 30 | 70 | 150 | 100 | 170 | 100 | 150 | 175 |
Вариант 20
х - средняя заработная плата (тыс. руб.);
у - прожиточный минимум на душу населения (тыс. руб.).
| x | 35,3 | 37,6 | 40,1 | 32, 6 | 45,2 | 42,8 | 48, 3 | 51,2 | 60,1 | 47,3 |
| y | 16,0 | 16,9 | 17,0 | 15,3 | 19,2 | 18,9 | 20,2 | 21,8 | 29,8 | 19,8 |
2. Множественная регрессия и корреляция
Задача 2. Изучается зависимость результирующего показателя y от факторов
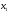 и
и 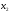
.
Требуется (для всех вариантов):
-
Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. -
Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. -
С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации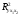 .
. -
С помощью частных F-критериев Фишера и t-статистики Стьюдента оценить целесообразность включения в уравнение множественной регрессии фактора после
после  и фактора
и фактора  после
после  .
. -
По возможности составить уравнение линейной парной регрессии , оставив лишь один значащий фактор.
Таблица 1 (для вариантов 1-10).
Обозначения и наименование показателей
производственно-хозяйственной деятельности предприятий
| Обозначение показателя | Наименование показателя |
| y1 | Производительность труда, тыс. руб./чел. |
| y2 | Индекс снижения себестоимости продукции |
| y3 | Рентабельность |
| x1 | Трудоемкость единицы продукции |
| x2 | Удельный вес рабочих в составе ППР |
| x3 | Удельный вес покупных изделий |
| x4 | Коэффициент сменности оборудования, смен |
| x5 | Премии и вознаграждения на одного работника ППР, тыс. руб. |
| x6 | Удельный вес потерь от брака, % |
| x7 | Фондоотдача активной части ОПФ, руб./руб. |
| x8 | Среднегодовая численность ППР, чел. |
| x9 | Среднегодовая стоимость ОПФ, млн. руб. |
| x10 | Среднегодовой фонд заработной платы ППР |
| x11 | Фондовооруженность труда, тыс. руб./чел. |
| x12 | Оборачиваемость нормируемых оборотных средств, дн. |
| x13 | Оборачиваемость ненормируемых оборотных средств, дн. |
| x14 | Непроизводительные расходы, тыс. руб. |
Вариант 1
| y1 | 9,4 | 9,9 | 9,1 | 5,5 | 6,6 | 4,3 | 7,4 | 6,6 | 5,5 | 9,4 | 5,7 | 5,2 | 10 | 6,7 |
| x1 | 0,23 | 0,43 | 0,26 | 0,43 | 0,38 | 0,42 | 0,3 | 0,37 | 0,34 | 0,23 | 0,41 | 0,41 | 0,22 | 0,31 |
| x3 | 0,4 | 0,19 | 0,44 | 0,25 | 0,02 | 0,06 | 0,15 | 0,24 | 0,11 | 0,47 | 0,2 | 0,24 | 0,54 | 0,29 |
Вариант 2
| y2 | 62 | 53,1 | 56,5 | 30,1 | 18,1 | 13,6 | 89,8 | 76,6 | 32,3 | 199 | 90,8 | 82,1 | 76,2 | 37,1 |
| x1 | 0,23 | 0,43 | 0,26 | 0,43 | 0,38 | 0,42 | 0,3 | 0,37 | 0,34 | 0,23 | 0,41 | 0,41 | 0,22 | 0,31 |
| x5 | 0,88 | 0,57 | 0,7 | 0,84 | 1,04 | 0,66 | 0,86 | 1,27 | 0,68 | 0,86 | 0,45 | 0,74 | 1,03 | 0,96 |