Лабораторная работа №2«Исследование резонансных явлений в линейных электрических цепях.»Цель работы – изучение основных свойств, законов и режимов работы линейных электрических цепей синусоидального тока. Экспериментальное определение значений параметров элементов, входящих в исследуемую цепь исследование их влияния на режим её работы. Экспериментальное исследование режимов резонанса напряжений и резонанса токов.

1. 
   Основные понятия и определения.
   

Реактивные индуктивные и емкостные сопротивления цепи перемененного тока могут уравновесить друг друга. В этом случае наступает режим работы называемый резонансом.При резонансе сопротивление цепи является чисто активным, угол сдвига фаз между током и напряжением равен нулю. Резонанс в цепи можно получить тремя способами: изменяя частоту напряжения цепи, индуктивность, емкость или и то и другое одновременно.Угловая частота при которой наступает резонанс, называется резонансной. Различают резонанс при последовательном соединении элементов цепи – резонанс напряжений и при параллельном – резонанс токов.

2. 
   Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений.
   

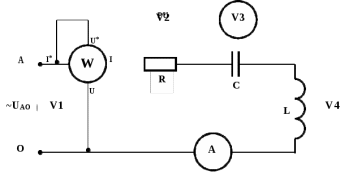
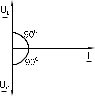
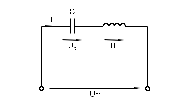
Когда по цепи (рис.2.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на конденсаторе U_C отстает от тока I на 90⁰, а напряжение на катушке индуктивности U_L опережает ток на 90⁰. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 180⁰). Рис.2.1 Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис.2.2), либо преимущественно емкостной (рис.2.3). Если напряжения U_LиU_С имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется

---

резонансом напряжений (рис.2.4).

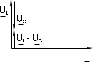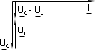Рис.2.2	Рис.2.3	Рис.2.4

При резонансе напряжений реактивное сопротивление цепи оказывается равным нулю.X = X_L – X_CПри заданных значениях L и C резонанс может быть получен путем изменения частоты.Поскольку X_L = L, а X_C = 1 / C, то резонансная частота ₀ может быть определена из уравнения:₀L – 1 / ₀C = 0,откуда 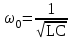и 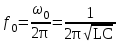.Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения U_L и U_C могут существенно (в десятки раз!) превышать приложенное напряжение.Частотными характеристиками обычно называют зависимости сопротивлений и проводимостей цепи от частоты синусоидального приложенного напряжения. 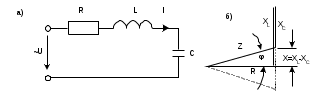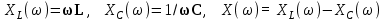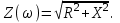Иногда к ним относят также зависимости от частоты токов, напряжений, фазовых сдвигов и мощностей.В последовательном резонансном контуре (рис.2.5а) активное сопротивление не зависит от частоты, а индуктивное, ёмкостное и реактивное сопротивления изменяются в соответствии со следующими выражениями: .Рис.2.5Полное сопротивление, как следует из треугольника сопротивлений (рис.2.5б):Вид этих зависимостей от частоты представлен на рис.2.6а. При резонансной частоте ₀=1/√(LC):X_L₀)=X_C₀)= √(L/C)=

---

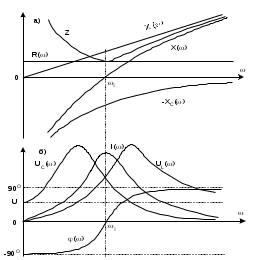
Это сопротивление называется характеристическим сопротивлением резонансного контура, а отношение/R=Q– добротностью резонансного контураНа рис.2.6б показаны графики изменения тока, напряжений на участках цепи и фазового сдвига при изменении частоты и неизменном приложенном напряжении в соответствии со следующими формулами:I()=U/Z); U_L()=LI(); U_C=I/C; φ=arctg[L-1/(CR)].Если Q>1, то при резонансе напряжения U_L(_) и U_C(_) превышают приложенное н апряжение в Q раз.Рис.2.6При <₀ цепь носит ёмкостный характер ( ток опережает напряжение на угол ), при =₀ - активный, а при >₀ - индуктивный (ток отстаёт от напряжения).

3. 
   Параллельное соединение конденсатора и катушки индуктивности.
   Понятие о резонансе токов.
   

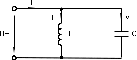
Когда к цепи (рис.3.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.Рис.3.1Общий ток цепи I разветвляется на ток в конденсаторе I_C (емкостная составляющая общего тока) и ток в катушке I_L(индуктивная составляющая общего тока), причем ток I_L отстает от напряжения U на 90⁰, а I_C опережает на 90⁰.Токи I_C и I_L имеют противоположные фазы (180⁰) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов (рис.3.2-3.4).Когда I_C = I_L и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис.3.2)

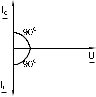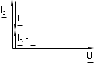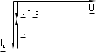Рис.3.2	Рис.3.3	Рис.3.4

---

Когда I_C  I_L, т.е. преобладает ток конденсатора, общий ток цепи I является по характеру емкостным и опережает напряжение U на 90⁰ (рис.3.3).Когда I_C I_L, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 90⁰ (рис.3.4).Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.При резонансе токов реактивная проводимость цепи B = B_L – B_C равна нулю. Резонансная частота определяется из уравнения 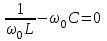,откуда, так же, как и при резонансе напряжений, и .Полная проводимость при резонансе токов оказывается близкой к нулю. Остается нескомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. 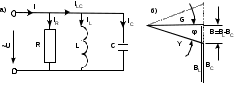Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи I_L и I_C могут превышать его в десятки раз.В параллельном резонансном контуре (рис.3.5а) активная проводимость не зависит от частоты, а индуктивная, ёмкостная и реактивная проводимости изменяются в соответствии со следующими выражениями:B_L()=1/ωL; B_C()=ωC; B()= B_L()- B_C();Рис.3.5Полная проводимость, как следует из треугольника проводимостей (рис.3.5б):Y()= 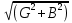Вид этих зависимостей от частоты представлен на рис.3.6а.При резонансной частоте ₀=1/ 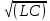:B_L(₀)=B_C(₀)= 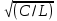=Эта проводимость называется характеристической проводимостью резонансного контура, а отношение

---

/G=Qтакже как и в последовательном контуре – добротностью. При изменении частоты и неизменном приложенном напряжении токи изменяются пропорционально соответствующим проводимостям:I()=UY); I_L()=U/L; I_C=UC, I_LC=UB().При резонансной частоте =₀ ток I, потребляемый от источника, имеет минимум и равен току в активном сопротивлении I_R, а ток на реактивном участке цепи I_LС равен нулю (см. рис.3.6а). Реальные кривые могут несколько отличаться от рассмотренных идеальных, так как здесь не учитывалось активное сопротивление катушки.Угол сдвига фаз (рис.3.6б) изменяется в соответствии с выражением:φ=arctg[(1/L-C)/G].При <₀ цепь носит индуктивный характер (ток отстаёт от напряжения на угол ), при =₀ - активный, а при >₀ - ёмкостный (ток опережает напряжение). Если Q>1, то при резонансе токов I_L(_) и I_C(_) превышают ток источника I в Q раз. Рис. 3.6На рис.3.6б кроме () построены также зависимости от частоты полного Z() и реактивного X() сопротивлений. B общем случае (см.сплошные линии на рисунке):Z()=1/Y()=1/√(G²+B²);X()=B/(G²+B²).При резонансе полное сопротивление принимает максимальное значение а реактивное обращается в ноль.В идеализированном случае, когда активная проводимость настолько мала, что ей можно пренебречь (G=0):X()=1/B; Z()=1/|B|.Тогда в точке резонанса кривые X() и Z() имеют разрыв (см. пунктирные линии на рис.3.6б).

4. 
   Частотные характеристики
   

последовательного резонансного контура.Исследование резонанса напряжений.Задание.Снимите экспериментально частотные характеристики последовательного резонансного контура Z(ɷ), Х(ɷ), I(ɷ), U_C(ɷ), U_L(ɷ), φ(ɷ).Порядок выполнения работы

---

Смотрите также файлы

• Конспект занятия по лепке способом пластилинографии Одуванчики для лесных зверят.docx

• Области применения теории решения изобретательских задач.rtf

• Задача философии 3 Каноника Эпикура 4 Физика Эпикура 6 Этика Эпикура 9 Атеизм Эпикура 11.doc

• Новосибирский государственный технический университет кафедра прочности летательных аппаратов.docx

• Предметные требования с овз прописывались по каждому предмету дополнительным блоком.docx