Файл: Решение. Интерференционный максимум в произвольной точке а экрана будет наблюдаться при разности хода, где (1).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
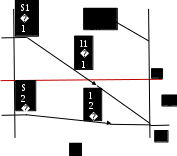
Задача 13.13. В опыте Юнга свет с длиной волны 600 нм падает на узкую щель, за которой расположены параллельные ей еще две щели
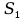 и
и 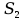 , расстояние между которыми равно 0,15 мм (рис. 13.12). Чему равно расстояние между двумя соседними интерференционными полосами, наблюдаемыми на экране, расположенном на расстоянии 90 см от щелей
, расстояние между которыми равно 0,15 мм (рис. 13.12). Чему равно расстояние между двумя соседними интерференционными полосами, наблюдаемыми на экране, расположенном на расстоянии 90 см от щелей 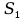 и
и 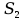 ?
?Дано:
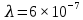 нм,
нм, 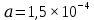 м,
м, 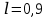 м;
м; 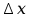 - ?
- ?Решение. Интерференционный максимум в произвольной точке А экрана будет наблюдаться при разности хода:
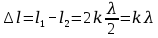 , где
, где 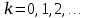 (1)
(1)Выразим
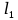 и
и 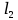 (см. рис. 13.12):
(см. рис. 13.12):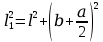 ,
, 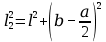 ,
, 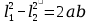 ,
, 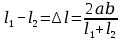 .
.Ввиду того что
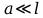 , можно считать
, можно считать 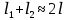 .
.Тогда
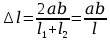 . (2)
. (2)Приравнивая уравнения (1) и (2), получим
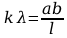 ,
, 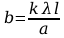 .
.Расстояние между нулевым (k=0) и первым (k=1) максимумами равно:
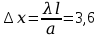 мм.
мм.Таким же будет расстояние между другими соседними интерференционными полосами.
Задача 13.14. В точку А на экране
, отстоящем от точечного источника света S на расстоянии 1,28 м, приходят два луча: один непосредственно от источника, другой после отражения от плоского зеркала B, параллельного лучу SA (рис. 13.13). Каким будет результат интерференции точки А, если длина волны равна 500 нм, а расстояние от луча SA до плоскости зеркала равно 4 мм?
Дано:
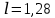 м,
м, 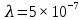 м,
м, 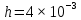 м.
м.Решение. Расстояние SBA равно:
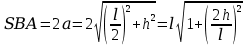 . (1)
. (1)Величина
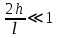 , поэтому можно воспользоваться формулой приближенных вычислений:
, поэтому можно воспользоваться формулой приближенных вычислений: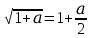 ,
, 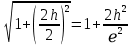 . (2)
. (2)Подставляя выражение (2) в уравнение (1), получим
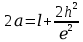
Геометрическая разность хода между двумя лучами равна
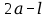 .
.При отражении в точке B от оптически более плотной среды теряется полуволна, поэтому оптическая разность хода лучей равна:
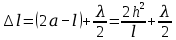
Найдем сколько полу волн укладывается на этой разности хода:
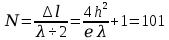 полуволна.
полуволна.