Файл: Окружности, описанная около треугольника и вписанная в треугольник.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 43
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Раздел: | Окружность. Геометрические построения | |
| ФИО педагога: | Юнусова А.В. | |
| Дата: | 27.04.2023 | |
| Класс: 7 | Количество присутствующих: | Количество отсутствующих: |
| Тема урока: | Окружности, описанная около треугольника и вписанная в треугольник | |
| Цели обучения в соответствии с учебной программой. | 7.1.2.14 знать определения окружностей, вписанной в треугольник и описанной около треугольника; | |
| Цели урока: | познакомить учащихся с понятиями вписанной и описанной окружностей треугольника и их свойствами | |
Ход урока
| Этапы урока/ время | Действия педагога | Действия ученика | Оценивание Рубрика | Ресурсы |
| Начало урока/ 2 мин | Приветствие. Сообщение темы, цели урока и ожидаемого результата | Записывают число и тему урока. Совместно с учителем формулируют цели урока. Настраиваются на положительный настрой урока. | | |
| Середина урока/ 38 мин | Актуализация знаний (2 мин) Устно: 1) Что такое окружность? 2) Дайте определение треугольника? 3) Что такое перпендикуляр? 4) Серединный перпендикуляр? 5) Что такое касательная? 6) Что такое биссектриса треугольника? Индивидуальная работа (9 мин) Решение направляющих задач 1. Постройте треугольник и проведите серединные перпендикуляры к каждой стороне. 2. Постройте треугольник и проведите биссектрисы его углов Изучение нового материала (4 мин) Ознакомления с новыми понятиями. Определение 1: Окружность, проходящую через вершины треугольника, называютописанной около треугольника. Чтобы найти центр описанной окружности около треугольника, надо построить серединные перпендикуляры к сторонам треугольника. Точка пересечения серединных перпендикуляров и является центром описанной окружности. ОА = ОВ = ОС = R. 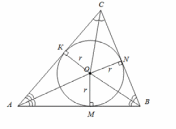 Групповая работа (9 мин) Цель которого сделать определенные выводы, укрепить навыки по построению и научится прислушиваться к другим ученикам. Ознокомление с теоремами: (3 мин) Теорема 1: Серединные перпендикуляры треугольника пересекаются в одной точке и является центром описанной около треугольника окружности. Теорема 2: Биссектрисы треугольника пересекаются в одной точке и является центром вписанного в треугольник окружности. Самостояетльно выполняют доказательства теорем с помощью заполнения пропусков в карточках Формативное оценивание Тест | Демонстрируют свои знания и умения Решают направляющие задачи Анализируют и записывают определения Разбирают совместно с учителем понятие описанной окружностей треугольника Распределяются на группы Укрепляют навыки по построению Ученики показывают умение обосновывать свое понимание Анализируют и записывают теоремы Выполняют самостоятельно теоретический тест | Взаимооценивание Формативное оценивание (за каждый правильный ответ 1 б) | Приложение 1 Приложение 2 |
| Конец урока / 5 мин | Рефлексия «дерево достижений» -Какую цель мы поставили сегодня на уроке? -Достигли мы целей, которые ставили в начале урока  Домашняя работа: | Анализируют деятельность на уроке «Красное яблоко» - урок прошел полезно, плодотворно (все понятно) «Желтое яблоко» - не все получилось, но я старался (хорошо) «Зеленое яблоко» - не смог справиться со всеми заданиями, еще нужно поработать (удовлетворительно). Ознакомляются с домашним заданием | Самооценивание | Стикеры |
Приложение 1
Группа А
Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите серединные перпендикуляры с каждой стороны. Ответьте на вопросы:
-
Пересекаются ли все серединные перпендикуляры в одной точке? -
Могу ли я построить окружность с центром в точке пересечения серединных перпендикуляров и проходящая через вершины треугольника? -
Как бы вы могли эту окружность назвать?
Группа В
Постройте треугольник со сторонами 7 см и 5 см и с углом между ними в 70 ̊ и проведите биссектрису с каждого угла треугольника. Ответьте на вопросы:
-
Пересекаются ли все биссектрисы в одной точке? -
Могу ли я построить окружность с центром в точке пересечения биссектрис и касающаяся сторон треугольника?
-
Как бы вы могли эту окружность назвать?
Приложение 2
Теорема 1: Серединные перпендикуляры треугольника пересекаются в одной точке и является центром описанной около треугольника окружности.
-
Постройте произвольный треугольник АВС. -
Проведите серединные перпендикуляры к сторонам АВ и АС пересекающиеся в точке D. -
Докажите, что DA = DB. -
Аналогично, DA = DС. -
Делаем вывод, что DС= DB, значит точка D _____________ от вершин С и B. То есть лежит на серединном перпендикуляре стороны СB. -
Значит точка D равно__________ от всех вершин треугольника. Соответственно является центром ________________ около треугольника окружности.
Теорема 2: Биссектрисы треугольника пересекаются в одной точке и является центром вписанного в треугольник окружности.
-
Постройте произвольный треугольник АВС. -
Проведите биссектрисы с вершин А и В пересекающиеся в точке L. -
Докажите, что точка L равноудалена от сторон АС и АВ. Аналогично, и от сторон BC и ВА. -
Делаем вывод, что точка L ______________ от сторон СА и СВ, значит точка L лежит на биссектрисе угла ___. -
Значит точка D равно__________ от всех сторон треугольника. Соответственно является центром ________________ в треугольник окружности.
Приложение 3
Тест
-
Центр окружности, вписанной в треугольник, совпадает с точкой … -
Если точка А равноудалена от сторон данного угла, то она лежит на … -
Если точка В лежит на серединном перпендикуляре, проведенному к данному отрезку, то она … -
Около любого … можно описать окружность -
Центр вписанной в равнобедренный треугольник лежит на … -
Центр окружности, описанной около треугольника, совпадает с точкой -
Если точка Д лежит на биссектрисе данного угла, то она …. -
Если точка С равноудалена от концов данного отрезка, то она лежит на… -
В любой … можно вписать окружность -
Центр описанной окружности около прямоугольного треугольника лежит…