ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 13
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Обнаружение объектов с использованием каскадных классификаторов – один из самых простых способов обнаружения объектов. Метод устарел и в наши дни используется редко, однако все еще считается эффективным и довольно быстрым. Его основная идея заключается в выделении объектов на изображении с помощью фильтра – в данном случае примитивов Хаара. Метод основан на машинном обучении, в процессе которого функция обучается на выборки из положительных и отрицательных изображений. Под положительными изображениями подразумеваются те, которые содержат целевой объект, под отрицательными – те, на которых его нет. Обучение каскадного классификатора требует достаточно большой выборки из таких изображений, но для достижения точности распознавания в 80% достаточно 500 положительных и 1000 отрицательных (соотношение положительных и отрицательных приятно брать как 1:2). Следующим шагом будет извлечение особенностей из этих изображений с помощью признаков Хаара. Эти признаки представляют собой двоичную аппроксимацию, двоичную маску – черное белое изображение и являются основой для выделения сложных. Другими словами, примитивы из прямоугольников, которые могут находиться в двух состояниях -1 и 1 (черное и белое). Признаки Хаара классифицируются на три группы: линейные, граничные и центральные. (Рис.2). Граничные служат для определения границ объекта, центральные – точечных деталей, линейные – вытянутых форм.
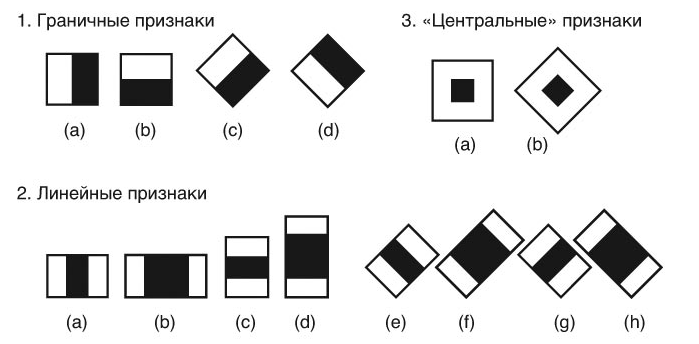
Рис.2. Классификация простых признаков Хаара.
Для получения этих примитивов с положительных изображений бинаризации области, использующий следующий алгоритм:
-
Берется область положительного изображения, где находится нужный нам объект. -
Эта область сильно уменьшается в размерах, для избавления от детализации (высоких частот). -
Далее, уменьшенная область из RGB режима в режим градации серого. Этим приемом уменьшается значение каждого нашего бита втрое. К примеру, если мы сжали нашу область до размера 10х10 пикселей, то каждому из них теперь соответствует лишь одно значение – значение серого. -
Находим среднее для всех пикселей. -
На основе среднего для каждого пикселя получаем 0, если его значение меньше среднего, и 1 – если больше.
Преимущества этого алгоритма заключаются в том, что ни масштабирование, не изменения яркости и контраста не сильно влияют на итоговый результат. Уже на основе таких примитивов будут формироваться классификаторы, называющиеся функциями Хаара. Каждая функция будет представлять собой отдельное значение веса, равное либо сумме пикселей под белыми и черными прямоугольниками, либо их отношению. (Последнее используется для уменьшения влияния масштабирования изображения). Для получения такой суммы пикселей используется метод оптимизации, называемы интегральным преобразованием изображения. Интегральное изображение – матрица, элементы которого хранят сумму ячеек выше и левее относительно них самих, включая и собственные их значения. Таким образов, вычисление сумма для прямоугольника на Рис.3 сводится к простой формуле А – (C + B + D). Алгоритм является очень быстрым, ведь для получения сумма мы обращаемся к памяти только 4 раза. Полученные на позитивных изображениях нашей выборки функции называются слабыми классификаторами. Такие функции принимают на вход изображения, вычисляют значение признака Хаара, сравнивают его с порогом и возвращают либо 0, либо 1. Далее, из этих слабых классификаторов составляются новые, сложные классификаторы, путем перебора все возможных слабых классификаторов и выбора из них тех, что допускают меньше всего ошибок, работающие дольше, но эффективнее. Значение порога сильного классификатора прямо пропорционально количеству неверно классифицированных хороших примеров и обратно пропорционально количеству неверно классифицированных плохих примеров. Это значит, что можно добиться минимального количества ложных негативных срабатываний за счет увеличения ложных положительных срабатываний.
Основываясь на данном принципе, формируется конечный каскад, состоящий из множества стадий, через которые последовательно будет проходить изображение. Стадия – набор признаков (сложных классификаторов). С каждой новой стадией формируются все более сложные классификаторы.
Каскадирование необходимо в первую очередь для того, чтобы увеличить скорость работы алгоритма, т.к. сложные классификаторы работают очень медленно.
Понятно, что объект не будет хорошо определяться в сложном классификаторе, если до этого он плохо определялся в более простом. Поэтому, по мере прохождения изображения через эти стадии, более сложные классификаторы будут применяться только к тем элементам изображения, которые хорошо определялись на предыдущих. Такой принцип гарантирует рациональную трату ресурсов.
Каждая стадия содержит в себе порог и критическое значение.
В процессе работы алгоритма, вдоль изображения начинает двигаться окно того же размера, что и наши примитивы. С каждым обходом окном изображения, его размеры увеличиваются на заданный шаг. Внутри каждого окна считается сумма яркостей sum и сумма квадратов яркостей пикселей ssq, из который вычисляются математическое ожидание m = sum * n, где n – нормировочный множитель, обратно пропорциональный количеству пикселей внутри движущегося окна, и дисперсия v = sqq * n – sqr(m). Из m и v вычисляется стандартное отклонение sd = sqrt(v), при v >= 0 или 1, при v < 0. Полученное стандартное отклонение сравнивается с пороговым значением, и если оно меньше него, то текущее окно отсеивается в самом начале и более не рассматривается за низкой вероятностью наличия в нем нужного объекта. Далее, для каждого окна на каждой стадии считается суммирующийся коэффициент, который сравнивается с критическим значением текущей стадии. В случае, если критическое значение больше, то стадия считается не пройденной, иначе, окно переходит на следующую. Когда окно проходит все стадии, считается, что в нем обнаружен искомый объект.
Данный метод каскадных классификаторов реализован в библиотеке OpenCV.
Для начала, нам нужно будет собрать выборку из положительных и отрицательных изображений, в нашем случае в соотношении 245/387. Далее формируем два текстовых файла (позитивные_примеры.dat, негативные_примеры.dat), в котором будут храниться пути к нашим изображениям. Для этого позитивные и негативные изображения группируем в папки, для удобства даем им одинаковые имена с индексациями (выделяем все изображения => F2 => даем новое имя первому файлу => жмем Enter), открываем данные директории в терминале/cmd и прописываем следующую команду:
dir /b>название_файла.txt
В файле с путями позитивных изображений необходимо напротив каждого указать количество объектов и координаты смежных вершин прямоугольной области, в которой расположен наш объект, поэтому, для удобства, лучше обрезать каждое позитивное изображение так, чтобы в нем находился один экземпляр нашего объекта, а координаты указать в виде 0 0 высота ширина.
Выглядеть должно следующим образом:

Далее, нам нужно создать вектор позитивных изображений. Для этого будем использовать программу
opencv_createsamples.exe расположенный в папке дистрибутива OpenCV. Запускаем ее через терминал, передавая ей необходимые параметры:
C:\Users\kosin\Downloads\opencv\build\x64\vc15\bin\opencv_createsamples.exe
-info C:\learning\goods\Cropper\goods.dat
-vec C:\my_samples.vec
-num 246
-w 50 -h 35
В первой строке указываем путь до нашей программы. Во второй строке параметру -info передаем полный путь файла со списком позитивных изображений. Далее в параметр -vec записываем имя файла – вектора, который мы хотим получить. Параметру -num передаем количество позитивных изображений, он не обязателен, но желателен во избежание ошибок. Все изображения нужно масштабировать и привести к общему размеру. Размер должен отражать примерные пропорции распознаваемого объекта, чем параметр меньше, тем быстрее в дальнейшем будет работать алгоритм. Их указываем в последней строке, где W – ширина, H – высота.
Результатом работы программы будет вектор положительных изображений, который будем использовать для обучения нашего каскада.
Для обучения каскада будем использовать программу opencv_traincascade.exe, расположенные там же, где и предыдущая.
Запускаем ее через терминал, передавая ей необходимые параметры:
C:\Users\kosin\Downloads\opencv\build\x64\vc15\bin\opencv_traincascade.exe
-data C:\test_cascade
-vec C:\my_samples.vec
-bg C:\learning\bads.txt
-numStages 25
-minhitrate 0.990
-maxFalseAlarmRate 0.4
-numPos 179 -numNeg 386 -w 70 -h 55 -mode ALL -precalcValBufSize 1024 -precalcIdxBufSize 1024
-
-data -путь до директории, куда будут сохраняться xml файла наших stage и итогового каскада. -
-vec -путь до нашего вектора положительных изображений -
-bg -файл с негативными изображениями -
-numStages -количество стадий итогового каскада, чем значение больше, тем медленнее будет проходить обучение и тем больше будет точность нашей модели. Стандартного указывают значения в диапазоне [15, 30] -
-minhitrate -пороговый коэффицент, показывающий позитивного примера. Как и говорилось ранее, чем оно выше, тем больше количество ложных негативных срабатываний. -
-maxFalseAlarmRate -уровень ложных срабатываний, по умолчанию ставят 0.5, значение напрямую зависит от minhitrate и качества нашей выборки. Чем оно выше, тем быстрее будет достигнут его значение при котором наше обучение закончится. -
-numPos -количество позитивных изображений. При высоком значении параметра minhitrate большее количество изображений будут считаться непригодными для обучения и пропускаться, поэтому, желательно указывать около 75% от всей положительной выборки. -
-numNeg -количество отрицательных примеров, указывается как есть. -
(-w -h) -размеры примитивов, указываются те же значения, что и при создании вектора изображений. -
-mode -при значении ALL использует весь набор признаков Хаара, обучение получается дольше, а результат – лучше. -
(-precalcValBufsize -precalcIdxBufsize) -количество выделяемой оперативной памяти.
По окончании обучения в указанной папке появятся xml файла стадий и самого каскада.
Их мы будем использовать в нашей программе, которую реализуем на языке python.
Импортируем библиотеку OpenCv:
import cv2
Создадим переменную video, в которую с помощью метода VideoCapture запишем наше тестовое видео, указывая к нему путь из директории нашего проекта.
В переменную cas_xml запишем наш каскадный файл для дальнейшей работы с ним.
video = cv2.VideoCapture('videos/test.mp4')
Т.к. видео – поток изображений, откроем бесконечный цикл по обработке кадров нашего видеопотока и добавим условия выхода из него.
while True:
flag, img = video.read()
img_gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
found = cas_xml.detectMultiScale(img_gray, minSize=(70, 55))
cnt_detected = len(found)
if cnt_detected > 0:
for(a, b, width, height) in found:
cv2.rectangle(img, (a, b), (a+width, b+height), (255, 0, 0), 2)
cv2.imshow('test', img)
if cv2.waitKey(50) & 0xFF == ord(' '):
break
В первой строке нашего цикла в переменную img сохраняем текущий кадр. Далее, в переменную img_gray сохраним копию img в градациях серого для увеличения скорости обработки кадра.
Found – список, который будет содержать данные распознанных объектов. Для получения этого списка применяем к нашему xml файлу метод detectedMultiScale(), которому передаем наше изображение в градациях серого, минимальные размеры объекта, другими словами, размеры окна, о которых говорилось ранее.
В переменную cnt_detected сохраняем длину нашего списка.
Далее проверяем, если cnt_detected > 0, то в цикле принимаем такие параметры, как координаты верхнего левого угла распознанного объекта, высоту и ширину, и передаем эти значения в метод rectangle(), рисующий прямоугольник уже на RGB кадре.
Метод imshow() выводит изображение на экран.
Последнее условие – условие выхода из бесконечного цикла. Метод waitKey() выполняет задержку программы на переданное ему время ms.