МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН ФИЛЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ОБРАЗОВАНИЯ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ «МИСИС» В ГОРОДЕ АЛМАЛЫК.


Лабораторная работа №4


Дисциплина: “ Маркшейдерия”


Выполнил: Студент гр.1-20

Умаралиев Отабек

Принял: доц. Мамаджанов М.М
АЛМАЛЫК-2023

ВАРИАНТ 21


Задача 1. Выразить значение угла 37°46'30'' в виде десятичной дроби

Решение. Используем расчетную формулу

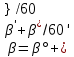
где β°. β' и β" - значение соответственно градусов, минут и секунд угла. Для условий данной задачи
B=37°+(46'+30"/60")/60' = 37,758°.
Задача 2. Выразить значения угла, заданного в виде 10,718333°, в градусах, минутах и секундах.

Решение. Вначале определяем числа минут и секунд, выраженные в секундах, как произведение
0,718333*3600"=2550".
Далее определяем число минут как частное
2550"/60"=42'.
При этом остаток, выраженный в секундах, должен быть меньше 60". Затем получаем окончательный результат: 10°42'30".
Задача 3. Вычислить географический азимут линии, расположенной в западной части зоны, если сближение меридианов равно 3°15', а дирекционный угол линии составляет 241°

Решение. Линия расположена в западной части зоны, поэтому значение сближения меридианов следует использовать со знаком "-". Географический азимут линии вычисляют по формуле (3):

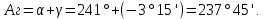
Задача 4. Определить географический азимут линии, если известно, что ее магнитный азимут составляет А_м = 136° при восточном склонении магнитной стрелки (δ =4°15').

Решение. Склонение магнитной стрелки восточное, значит, величину δ следует брать со знаком "+". Географический азимут определяют по формуле (2):

---

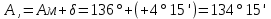
Задача 5. Определить значение румба линии, если ее дирекционный угол равен 301°.

Решение. Табличное значение румба определяют по формуле

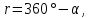
где α - дирекционный угол линии. Для условий задачи
.
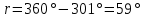С учетом обозначения координатной четверти по сторонам горизонта запишем окончательную величину румба: r = СЗ:60°.
Задача 6. Определить табличное значение угла, если дирекционный угол линии α = 336°.
Решение. Если α = 335°, то значение румба r = СЗ:25° (IV координатная четверть). Таким образом, табличный угол составит r= 24°.
Задача 7. Что означает Х_A = 6063 км и Y_A = 5675 км?

Решение. Точка A находится на расстоянии 6063 км к северу от экватора, в 5-й зоне и на расстоянии 675 км к востоку от осевого меридиана.
Задача 8. Определить географические координаты точки с прямоугольными координатами X = 0 км и Y = 9500 км.

Решение. Данная точка расположена на осевом меридиане 7-й зоны (в значении Y = 9500 цифра 9 указывает на номер зоны−N= 9, а действительная величина ординаты составляет Y = 500- 500=0 км). Таким образом, для точки осевого меридиана 9-й зоны географическая долгота составляет 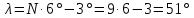. Поскольку X = 0 км, то следует принять, что точка находится на экваторе, т.е. ее географическая широта будет равна нулю (φ = 0°). Следовательно, для рассматриваемой точки имеем λ = 51° и φ= 0°.
Задача 9. Установить высоту точки C, если известно, что высота точки D равна 207,4 м, а превышение между точками по направлению от D к С составляет h=-12,6 м.

Решение. В соответствии с формулой (12) получаем
H_C=H_D-h= 207,4 - (-12,6) = 220,0 м.
Задача 10. Определить приращение координат по оси Y, если известно, что дирекционный угол линии α = 231°, а ее горизонтальная проекция d=70 м.

Решение. Поскольку α = 231°, то румб r = 50° (III четверть - ЮЗ) и, следовательно, приращение ∆Y должно быть со знаком "". Его значение вычисляем по формулам (8), (9):
∆Y = -d sinα = -d sin r = -70∙sin 50°= -53.6 м.
Задача 11. Вычислить дирекционный угол α для значения ∆Х = -121 м и ∆Y=+100 м.

---

Решение. По одной из формул обратной геодезической задачи вычисляем значение румба:

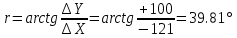
Учитывая, что приращение координат имеют знаки соответственно для ∆Y "+" и для ∆X "-" (II четверть), определяем дирекционный угол:
α = 180° - 39.81° = 140,19°.
Задача 12. Определить значение абсциссы точки В, если известно, что X_A = 500 м, горизонтальная проекция d_AB = 141 м и дирекционный угол α_AB =240°.

Решение. Поскольку α_AB = 141°, то румб линии АВ составляет r_AB = 40° (III четверть - ЮЗ) и, следовательно, приращение ∆Х будет иметь знак "-". Его значение вычисляем по формуле
∆X = d cosα =- d_AB cos r_AB = -141∙cos40° = -107.25 м,
тогда абсцисса В в соответствии с одной из формул прямой геодезической задачи составляет
X = X_A + ∆Х = 500 м + (-70 м) = 430 м.
Задача 13. Установить величину горизонтальной проекции d для значений:1) ∆Y = +100 м и α= 50°; 2) ∆Х = -200 м и α= 140°; 3) ∆Х =50 м и ∆Y =40 м.

Решение. 1. Для значений ∆Y= +100 м на α = 50° используем формулу (11) в виде
d = ∆Y/sinα = 100/sin 50° = 130.54 м.
2. Для значений ∆Х = -200 м и α= 140° используем формулу (11) в виде
d = ∆Х /cos α = -200/cos140° = 261.1 м.
3. Для значений ∆Х = 50 м и ∆У= 40 м используем формулу (11) в виде

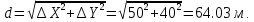
Задача 14. Определить длину и угол наклона линии, если известны координаты и высоты се точек А и В: Х_A =21, Y_A = 21, Н_A = 21 н Хв = 100 м, Yв = 100 м, Нв=200 м.

Решение. Для получения требуемых результатов используем формулы (13)−(15). После подстановки исходных данных задачи в расчетные формулы получаем
;

.
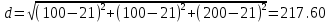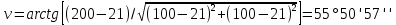Задача 15. Вычислить значение наклонной длины l для горизонтального проложения 100 м и угла наклона ν = 81°.

Решение. Величину / определяем по формуле
l =d/cosv=100 м/0,174 = 574,71 м.

---

Смотрите также файлы

• Основные функции эмоций.docx

• Лекция 11 1 Задания дать определения понятиям.docx

• Экзаменационная работа по математике. Фамилия.doc

• Тема Нормативноправовые основы деятельности педагога по физической культуре.docx

• СанктПетербургский государственный университет телекоммуникаций им проф. М. А. БончБруевича.docx